单视图度量（Single View Metrology）总结-编程知识

单视图度量（Single View Metrology）总结

news/2025/2/15 15:06:58/文章来源:https://www.cnblogs.com/isletfall/p/18716036

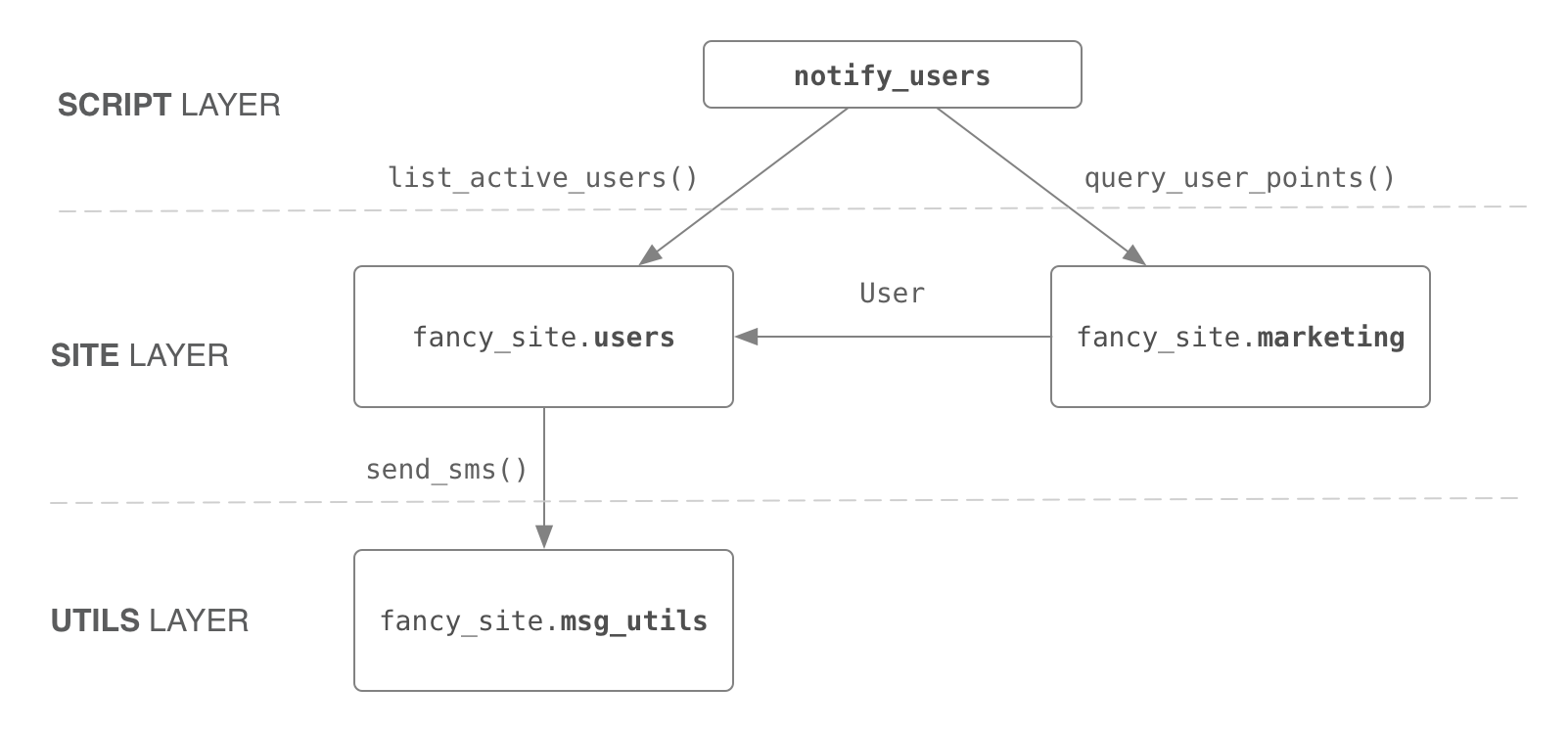
前面我们介绍了标定相机，并且我们知道，如果我们能够确定三维点的坐标以及标定相机的参数，就能够确定它在图像平面的位置。那我们现在思考一个问题，如果我们知道图像平面的坐标以及标定相机的参数，我们能够确定这个三维点的位置吗？

答案是否定的。因为一般情况下，三维点可以在由相机光心和投影点所确定的直线上的任何位置，因此仅通过单张图像上的投影点无法唯一确定三维空间中的点的位置。

因此，本节课我们将会介绍如何从三维世界中恢复结构。

二维变换（Transformation in 2D）

等距变换（Isometries）

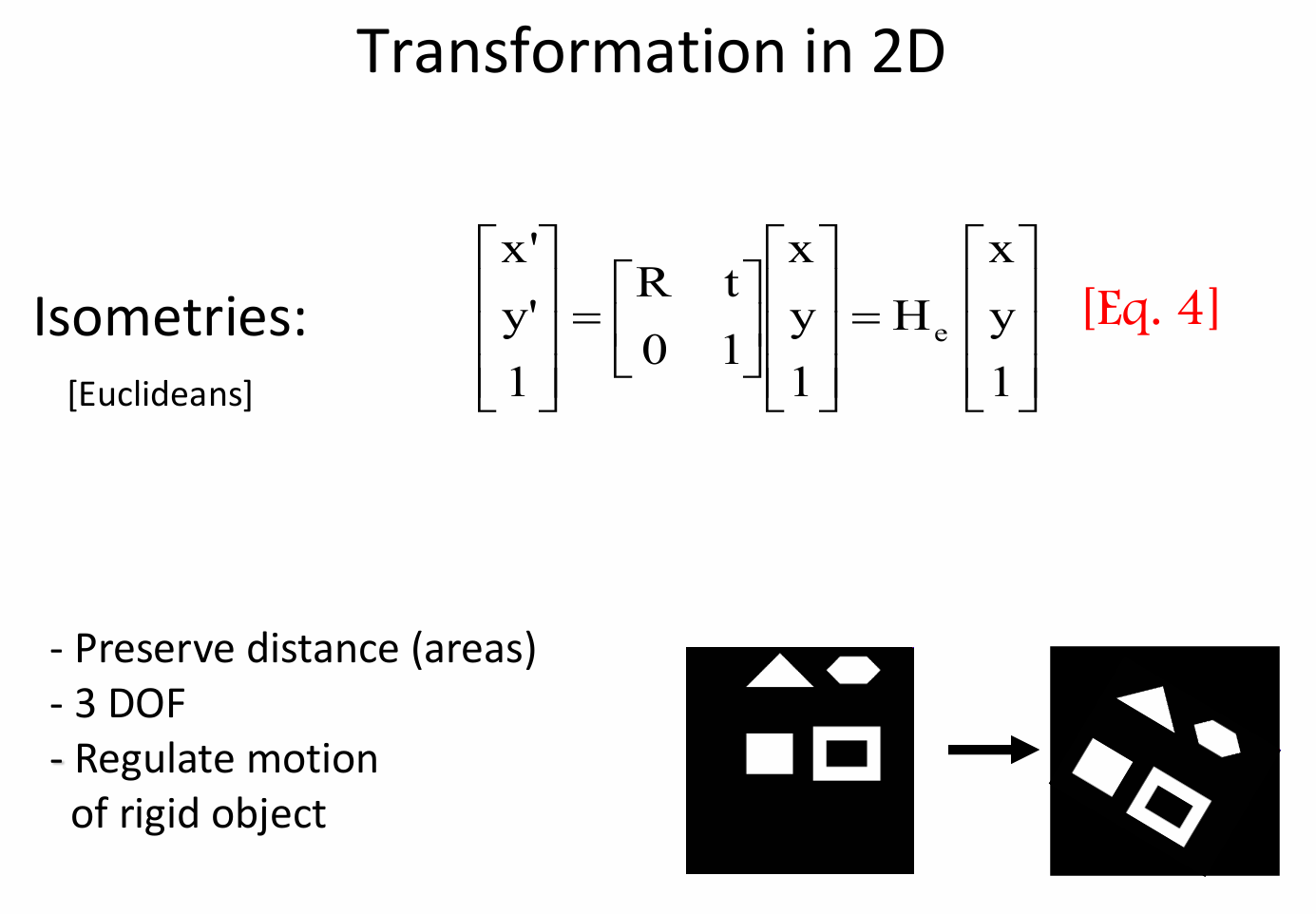
等距变换也叫欧式变换，它的齐次坐标矩阵形式为 $\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}R&t\\0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=H_e\begin{bmatrix}x\\y\\1\end{bmatrix}$
，其中 $R$ 是旋转矩阵， $t$ 是平移向量， $H_e$ 是欧几里得变换矩阵。这种形式用于将原坐标 $(x,y)$ 变换为新坐标 $(x',y')$。

等距变换的性质

Preserve distance (areas)：即保持距离（面积）不变，这是等距变换的一个重要特性，变换前后图形的距离和面积关系保持恒定。
3 DOF：表示有3个自由度（Degree - of - Freedom），通常对应二维空间中刚体运动的两个平移自由度（沿 (x) 轴和 (y) 轴方向的平移）和一个旋转自由度（绕垂直于平面的轴旋转）。
Regulate motion of rigid object：说明等距变换用于描述刚体的运动，刚体在二维平面中的运动可以通过这种变换来进行建模和分析。

相似变换（Similarities）

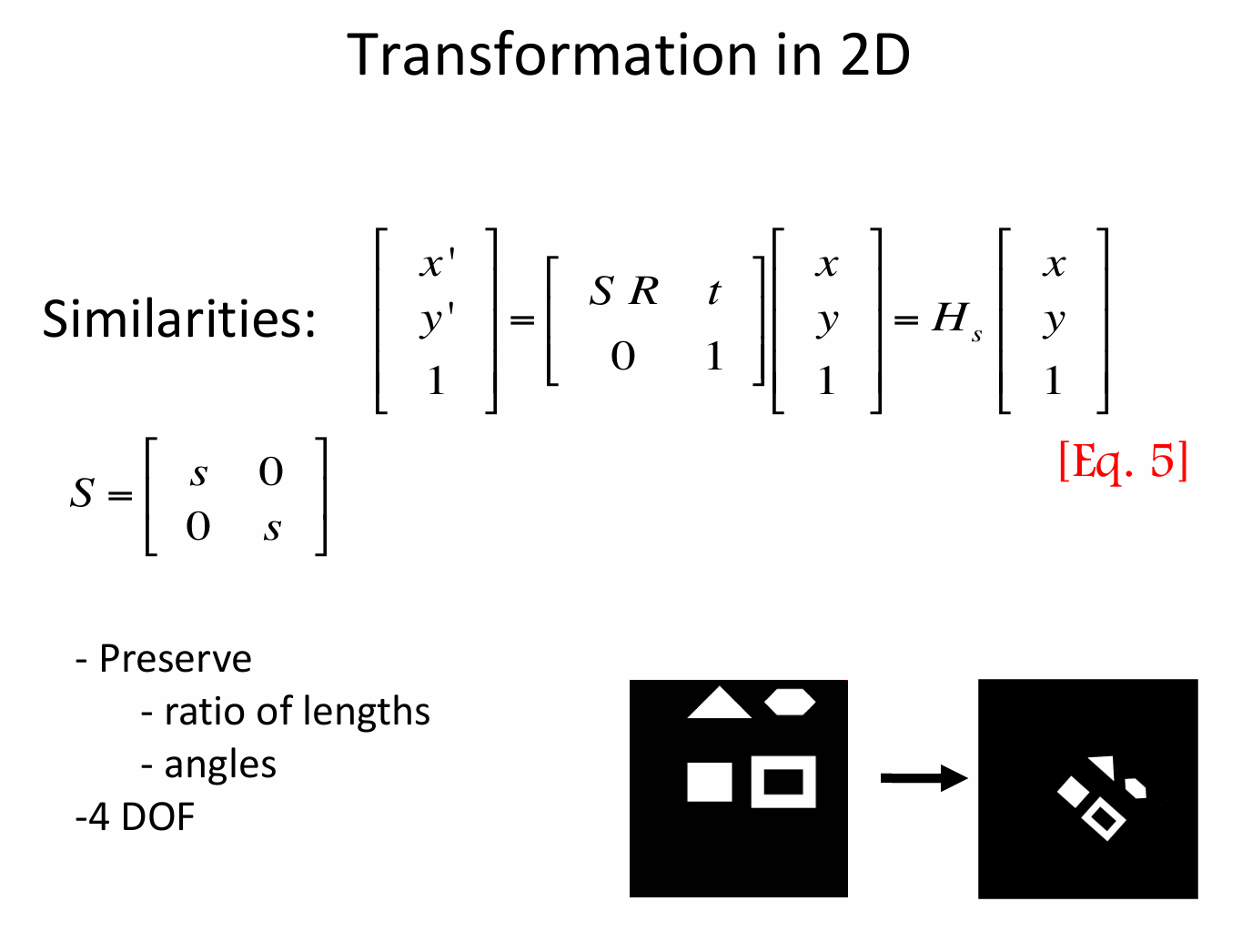
相似变换就是在等距变换的基础上允许图像进行缩放，它的齐次坐标矩阵形式为：$\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}SR&t\\0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=H_s\begin{bmatrix}x\\y\\1\end{bmatrix}$，其中 $S=\begin{bmatrix}s&0\\0&s\end{bmatrix}$，$s$ 是缩放因子，这种形式用于将原坐标 $(x,y)$ 变换为新坐标 $(x',y')$。。

相似变换的性质

Preserve ratio of lengths - angles：即保持长度比例和角度不变。这意味着相似变换前后，图形的形状保持相似，对应线段的长度比例恒定，对应角度相等。
4 DOF：表示有 4 个自由度（Degree - of - Freedom）。相比等距变换，除了二维空间中刚体运动的两个平移自由度和一个旋转自由度外，增加了一个缩放自由度。

仿射变换（Affinities）

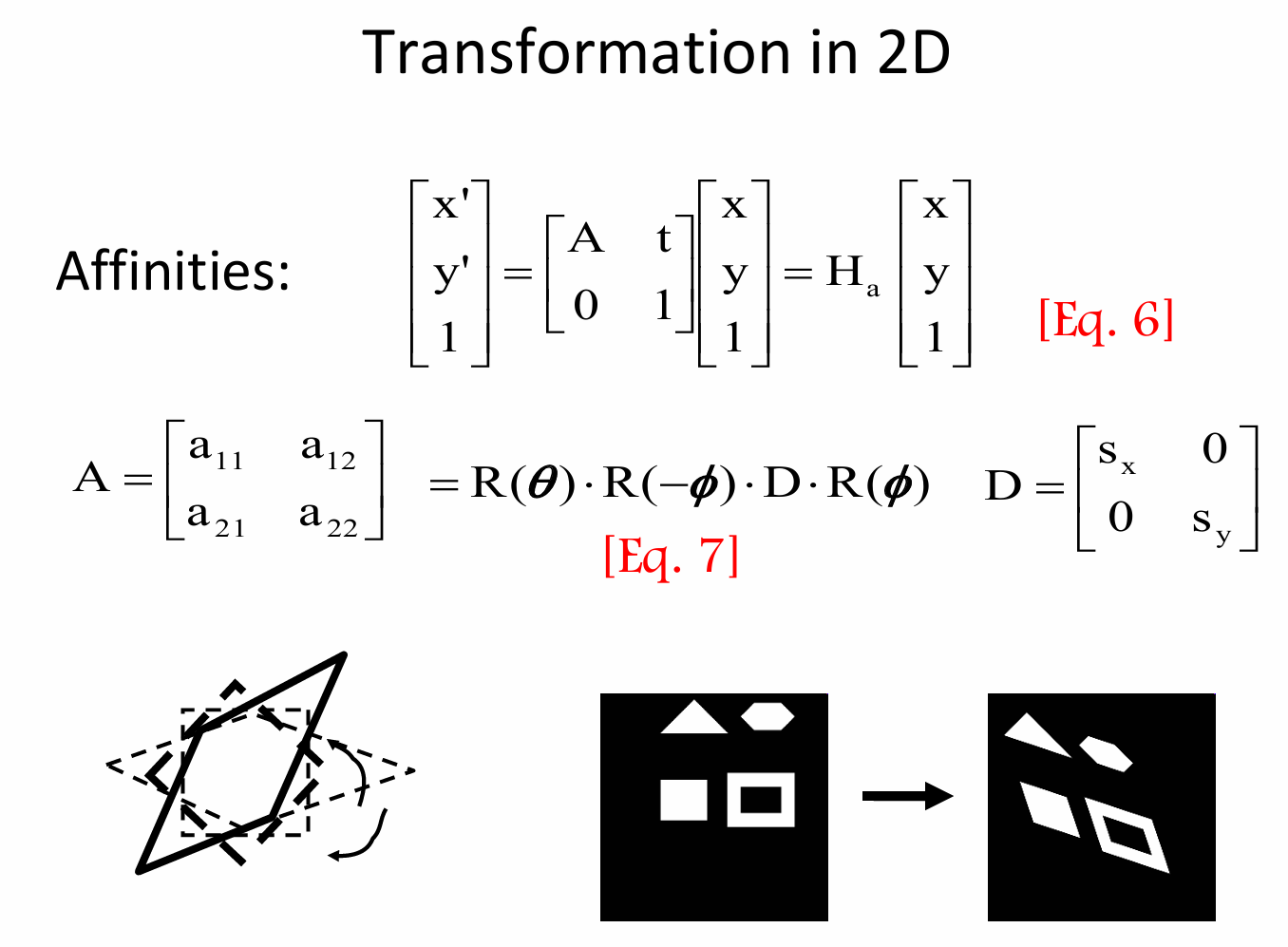
与前两种变换相比，仿射变换较为复杂，仿射变换的齐次坐标矩阵形式为 $\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}A&t\\0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=H_a\begin{bmatrix}x\\y\\1\end{bmatrix}$，其中 $A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}$ 是一个 $2\times2$ 的线性变换矩阵， $t$ 是平移向量， $H_a$ 是仿射变换矩阵。
这个 $A$ 矩阵是什么呢？ $A = R(\theta)\cdot R(-\phi)\cdot D\cdot R(\phi)$ ，其中 $D=\begin{bmatrix}s_x&0\\0&s_y\end{bmatrix}$ 是缩放矩阵（ $s_x$ 和 $s_y$ 分别是 $x$ 和 $y$ 方向的缩放因子）， $R(\theta)$ 、 $R(-\phi)$ 和 $R(\phi)$ 是旋转矩阵。这种分解表明仿射变换可以看作是旋转、缩放等基本变换的组合。

仿射变换的性质

保持平行线关系不变，即原本平行的直线在仿射变换后仍然平行。
保持面积比例不变。
保持共线线段的长度比例不变等。
具有6个自由度。

除了按照上面根据平移旋转进行分解，我们还有另外一种分解方法，即通过奇异值进行分解 $A=UDV^T=UV^TVDV^T=(UV^T)(V)(D)(V^T)$，则我们就能将其分解成四个矩阵的乘积，每个矩阵都能够与上面的旋转矩阵和缩放矩阵对应，从而进行求解。

射影变换（Projective）

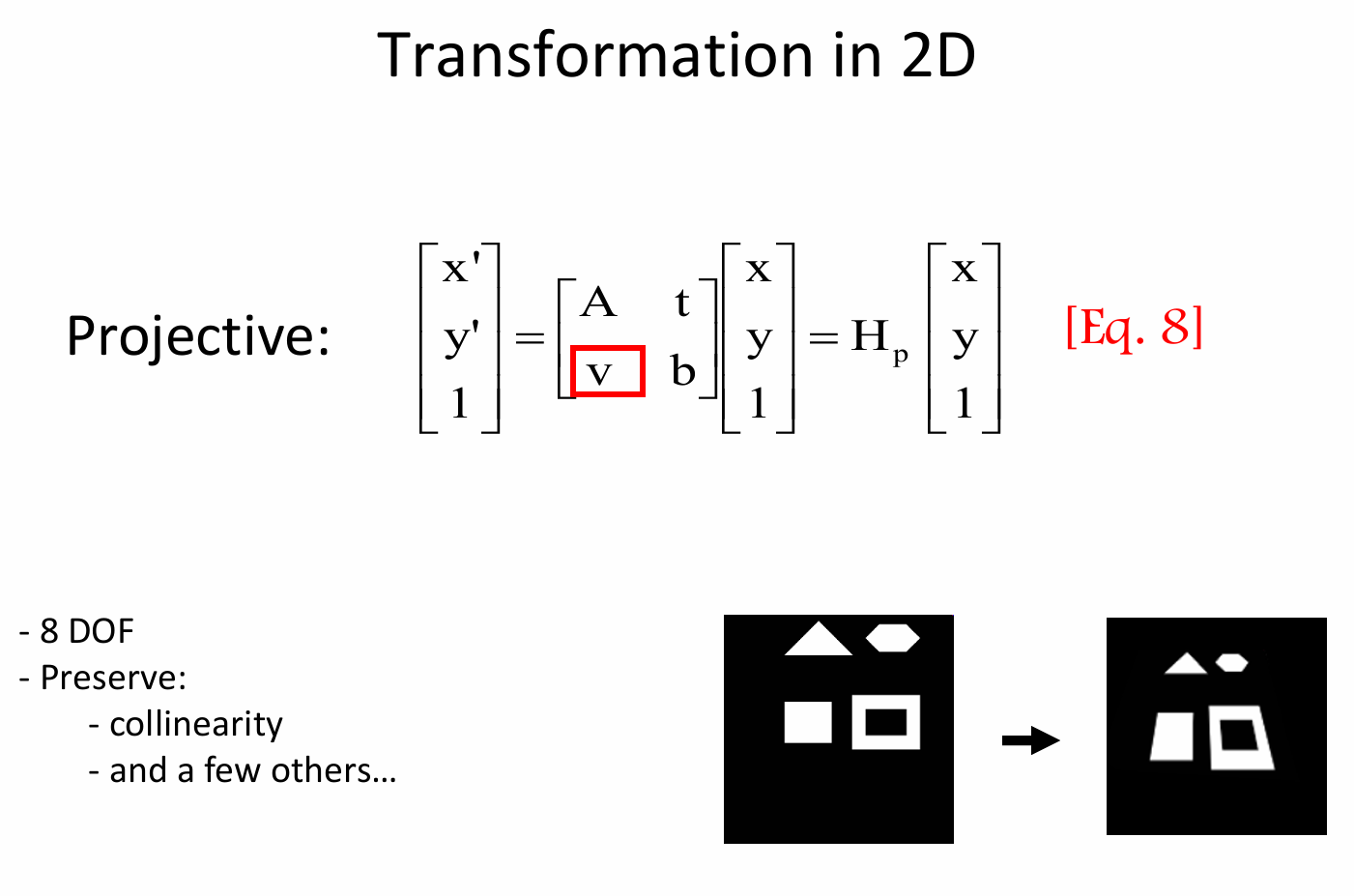
射影变换相较于仿射变换有更高的自由度，它在齐次坐标下的矩阵运算形式：$\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}A&t\\v&b\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=H_p\begin{bmatrix}x\\y\\1\end{bmatrix}$ 。其中 $A$ 是 $2\times2$ 矩阵，$t$ 是二维平移向量，$v$ 是二维行向量，$b$ 是标量，$H_p$ 是射影变换矩阵。这种形式比仿射变换等更具一般性。

射影变换的性质：

射影变换具有8个自由度（8 DOF）。这意味着有8个独立参数可用于定义该变换，相比前面介绍的等距变换、相似变换和仿射变换，它的自由度更高，能描述更复杂的变换关系。
射影变换保持共线性（collinearity），即原本共线的点在射影变换后仍然共线。

消影点和消影线（Vanishing points and lines）

对于一个二维平面上的直线，我们通常有一般形式： $ax+by+c=0$，并且我们可以知道直线的斜率是 $-\frac ab$，在 $y$ 轴上的截距为 $-\frac cb$，但是这样的表示方法在计算机中不够直观，无法直接用于处理直线相关的几何计算和判断。因此，人们想出了另外一种表示直线的方法用向量形式表示直线，将直线方程的系数组成向量 $\mathbf{l}=\begin{bmatrix}a\\b\\c\end{bmatrix}$。

这种表示方法能为我们带来许多好处，比如如果一个点 $[x_1,x_2]^T$ 位于直线 $\mathbf{l}$ 上，那么就会满足等式 $\begin{bmatrix}x_1\\x_2\\1\end{bmatrix}^T\begin{bmatrix}a\\b\\c\end{bmatrix}=0$

此外，这种形式能够帮助我们计算两条直线的交点，如果两条直线分别为 $l$ 和 $l'$ 那么他们的交点 $x=l\times l'$，证明如图所示：

二维点的表示

我们前面介绍过，对于一般的二维点，如果我们需要把齐次坐标形式转为非齐次坐标，只需要把坐标除以第三维即可，因此对于普通二维点，我们用三维向量 $\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$ 来表示，其中 $x_3 ≠ 0$。

但是如果第三维是零，那么我们就无法将其转化非非齐次坐标的形式了，那这种表示是什么含义呢？我们把这种点定义为无穷远点，即 $x_∞=\begin{bmatrix}x_1\\x_2\\0\end{bmatrix}$

平行线的表示

对于两条平行线 $l=\begin{bmatrix}a\\b\\c\end{bmatrix}$ 和 $l'=\begin{bmatrix}a'\\b'\\c'\end{bmatrix}$，由于平行这一条件，则有 $-\frac ab =-\frac{a'}{b'}$，同时在齐次坐标下，我们是可以求出两条平行线的相交点的，相交点为 $l\times l'=\begin{bmatrix}b\\-a\\0\end{bmatrix}$，这也说明两条平行线的交点是无穷远点。

同时，我们也可以得到一个关于直线和无穷远点的式子，如果直线 $l=[a,b,c]^T$ 经过无穷远点 $x_∞=[b,-a,0]^T$，则有 $l^Tx_∞=[a,b,c]\begin{bmatrix}b\\-a\\0\end{bmatrix}=0$。

无穷远直线

我们认为，所有的无穷远点都位于一条直线上，这条直线被称为无穷远直线，它的形式为 $l_∞=\begin{bmatrix}0\\0\\1\end{bmatrix}$，因为 $\begin{bmatrix}x_1\\x_2\\0\end{bmatrix}^T\begin{bmatrix}0\\0\\1\end{bmatrix}=0$，说明无穷远点都位于这条直线上。

无穷远点和无穷远线的射影变换

我们知道一般的射影变换矩阵 $H = \begin{bmatrix}A & t \\ v & b\end{bmatrix}$ ，其中 $A$ 是一个 $2\times2$ 的矩阵，$t$ 是二维向量，$v$ 是二维行向量，$b$ 是一个标量，如果我们对一般点实现射影变换，则有 $p' = Hp$ 。现在我们需要对于无穷远点 $p_{\infty}$ ，计算 $Hp_{\infty}$ ，将 $p_{\infty}=\begin{bmatrix}1 \\ 1 \\ 0\end{bmatrix}$ 代入 $H$ 进行矩阵乘法运算：$Hp_{\infty}=\begin{bmatrix}A & t \\ v & b\end{bmatrix}\begin{bmatrix}1 \\ 1 \\ 0\end{bmatrix}=\begin{bmatrix}p'_x \\ p'_y \\ p'_z\end{bmatrix}$ ，结果表明经过一般射影变换后，该点不再是无穷远点。

但是如果是仿射变换，结果又会有所不同。给出仿射变换矩阵 $H_A=\begin{bmatrix}A & t \\ 0 & b\end{bmatrix}$ ，计算 $H_Ap_{\infty}$ ，将 $p_{\infty}=\begin{bmatrix}1 \\ 1 \\ 0\end{bmatrix}$ 代入 $H_A$ 进行矩阵乘法运算：$H_Ap_{\infty}=\begin{bmatrix}A & t \\ 0 & b\end{bmatrix}\begin{bmatrix}1 \\ 1 \\ 0\end{bmatrix}=\begin{bmatrix}p'_x \\ p'_y \\ 0\end{bmatrix}$ ，结果表明在仿射变换下，无穷远点仍然是无穷远点。

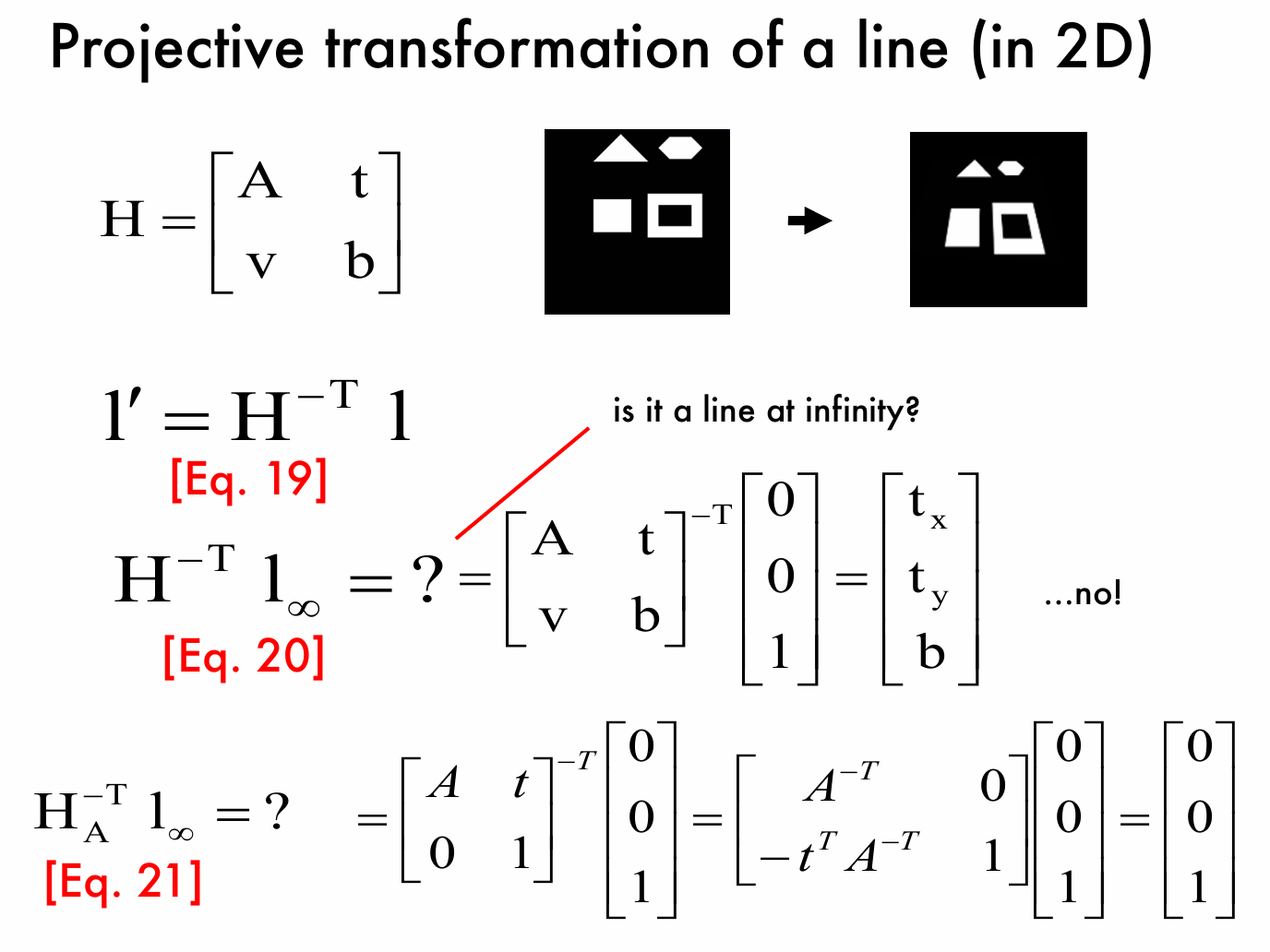
对于直线的射影变换公式为： $l'=H^{-T}l$，则对于无穷远线应用该公式，计算 $H^{-T}l_{\infty}$ ，将 $l_{\infty}=\begin{bmatrix}0 \\ 0 \\ 1\end{bmatrix}$ 代入 $H^{-T}=\begin{bmatrix}A & t \\ v & b\end{bmatrix}^{-T}$ 进行矩阵乘法运算，结果表明经过一般射影变换后，无穷远直线不再是无穷远直线。

而对于仿射变换矩阵 $H_A=\begin{bmatrix}A & t \\ 0 & 1\end{bmatrix}$ ，计算 $H_A^{-T}l_{\infty}$ ，将 $l_{\infty}=\begin{bmatrix}0 \\ 0 \\ 1\end{bmatrix}$ 代入 $H_A^{-T}=\begin{bmatrix}A & t \\ 0 & 1\end{bmatrix}^{-T}$ 进行矩阵乘法运算，结果表明在仿射变换下，无穷远直线仍然是无穷远直线。

三维点和平面

与二维点的定义类似，我们定义三维点为 $\begin{bmatrix}x_1\\ x_2 \\ x_3\\1\end{bmatrix}$，定义平面为 $\Pi=\begin{bmatrix}a\\ b \\ c\\d\end{bmatrix}$ 表示平面 $ ax+by+cz+d=0$，与二维点类似，如果点在平面上，则有 $x^T\Pi=0$

由于三维空间中的直线具有 4 个自由度，这使得在三维空间中表示直线较为困难，我们把直线可以定义为两个平面的交线。我们在这里定义直线的方向向量 $\mathbf{d}=[a,b,c]^T$ 表示直线的方向，其中 $a,b,c$ 为向量的分量。

与二维点类似，三维世界中的无穷远点也能写做 $\begin{bmatrix}x_1\\ x_2 \\ x_3\\0\end{bmatrix}$

3D中的消影点和消影线（Vanishing points and lines）

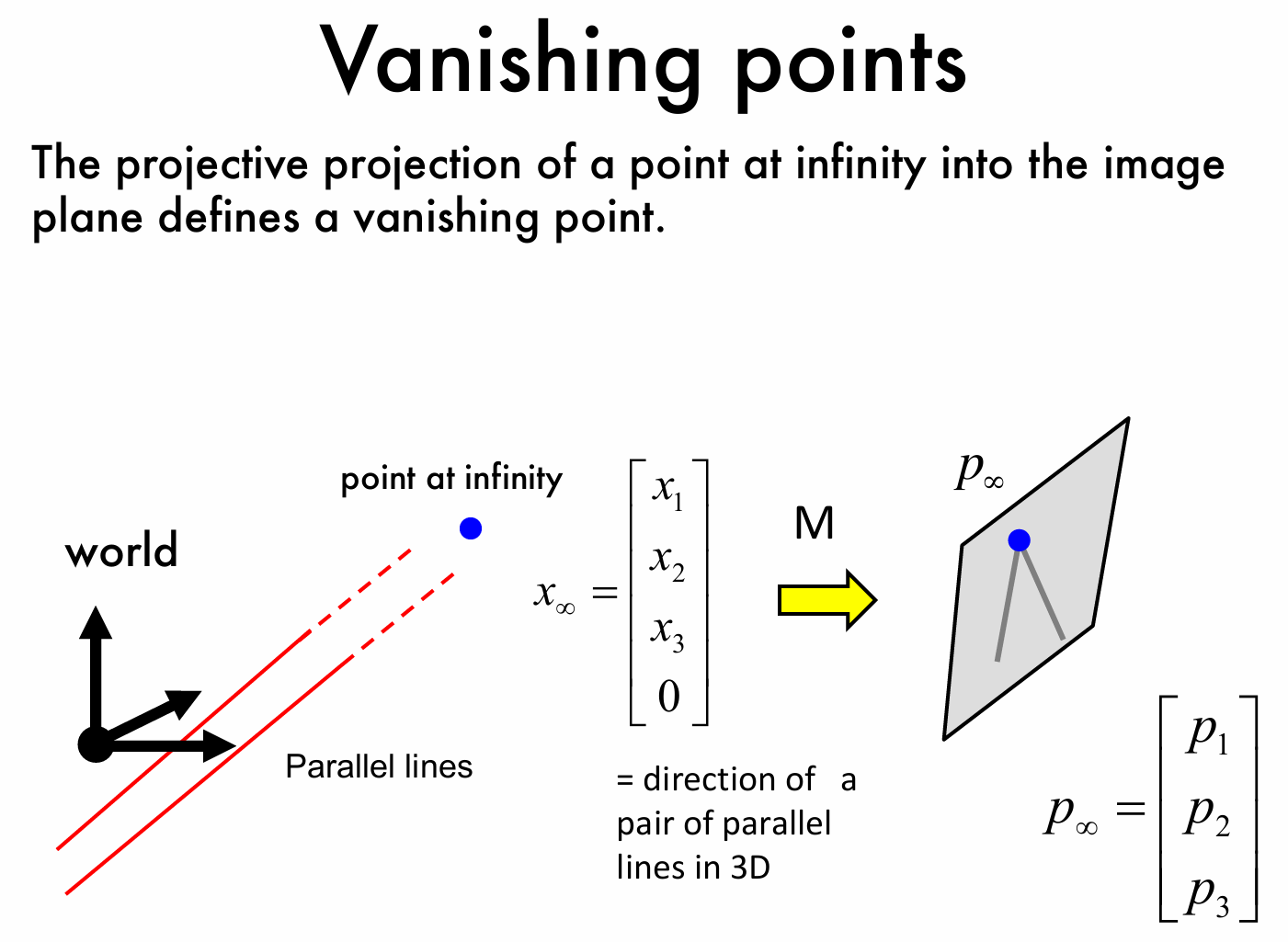
如图所示，世界坐标系中有两条平行的直线，这组平行线对应的无穷远点用蓝色点表示，其齐次坐标形式为
$\begin{bmatrix}x_1\\ x_2 \\ x_3\\0\end{bmatrix}$，该无穷远点代表了这组平行线的方向。通过射影变换，我们将其投影到图像平面上，无穷远点在图像平面上的对应点为 $p_∞=\begin{bmatrix}p_1\\ p_2 \\ p_3\end{bmatrix}$，这个点就是消影点，但是它不一定在无穷远了。

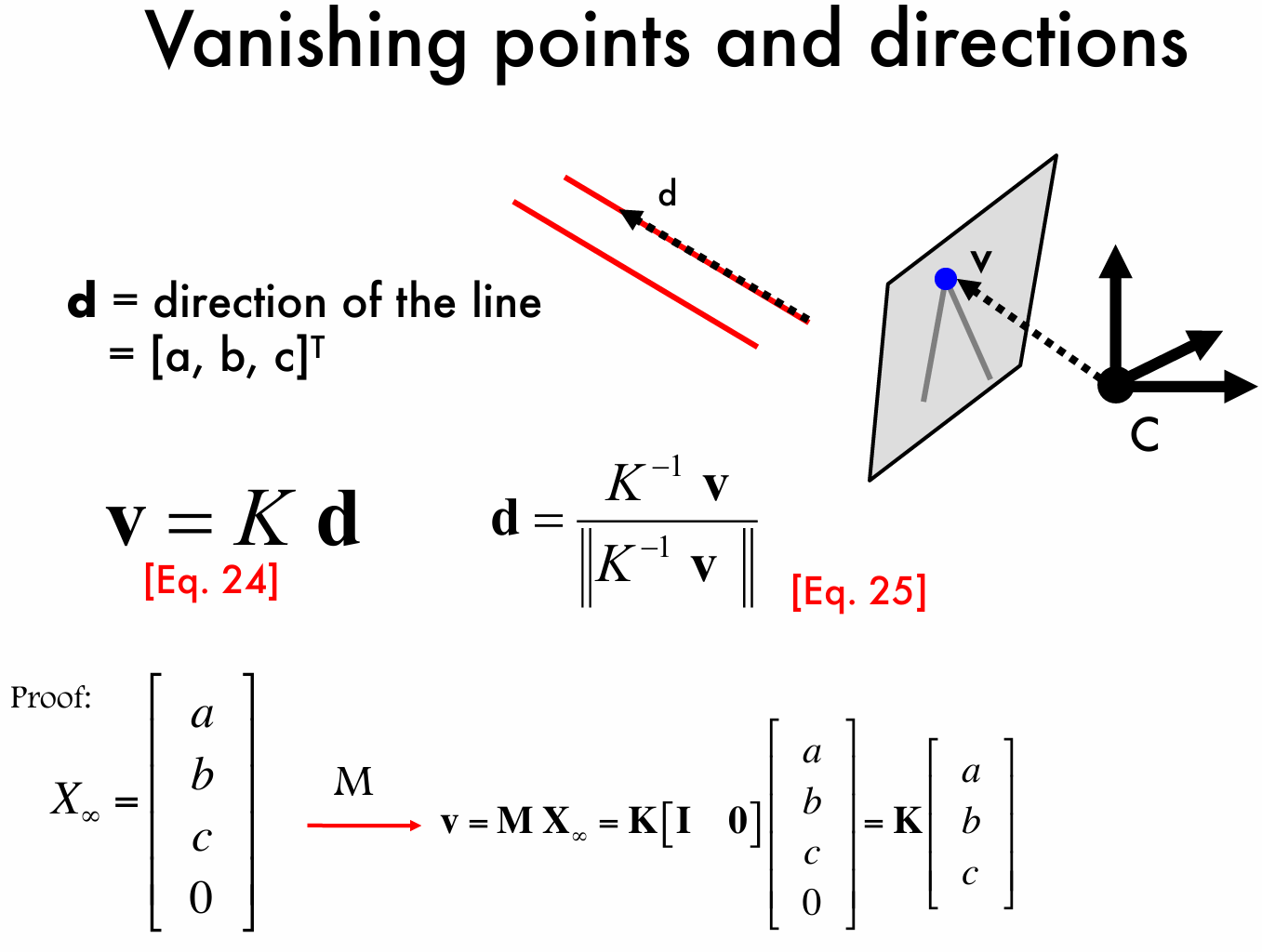
除此之外，直线的方向向量和消影点能够互相表示，即 $\mathbf{v}=K\mathbf{d}$，同样有 $\frac{K^{-1}\mathbf{v}}{\|K^{-1}\mathbf{v}\|}$，证明如图所示：

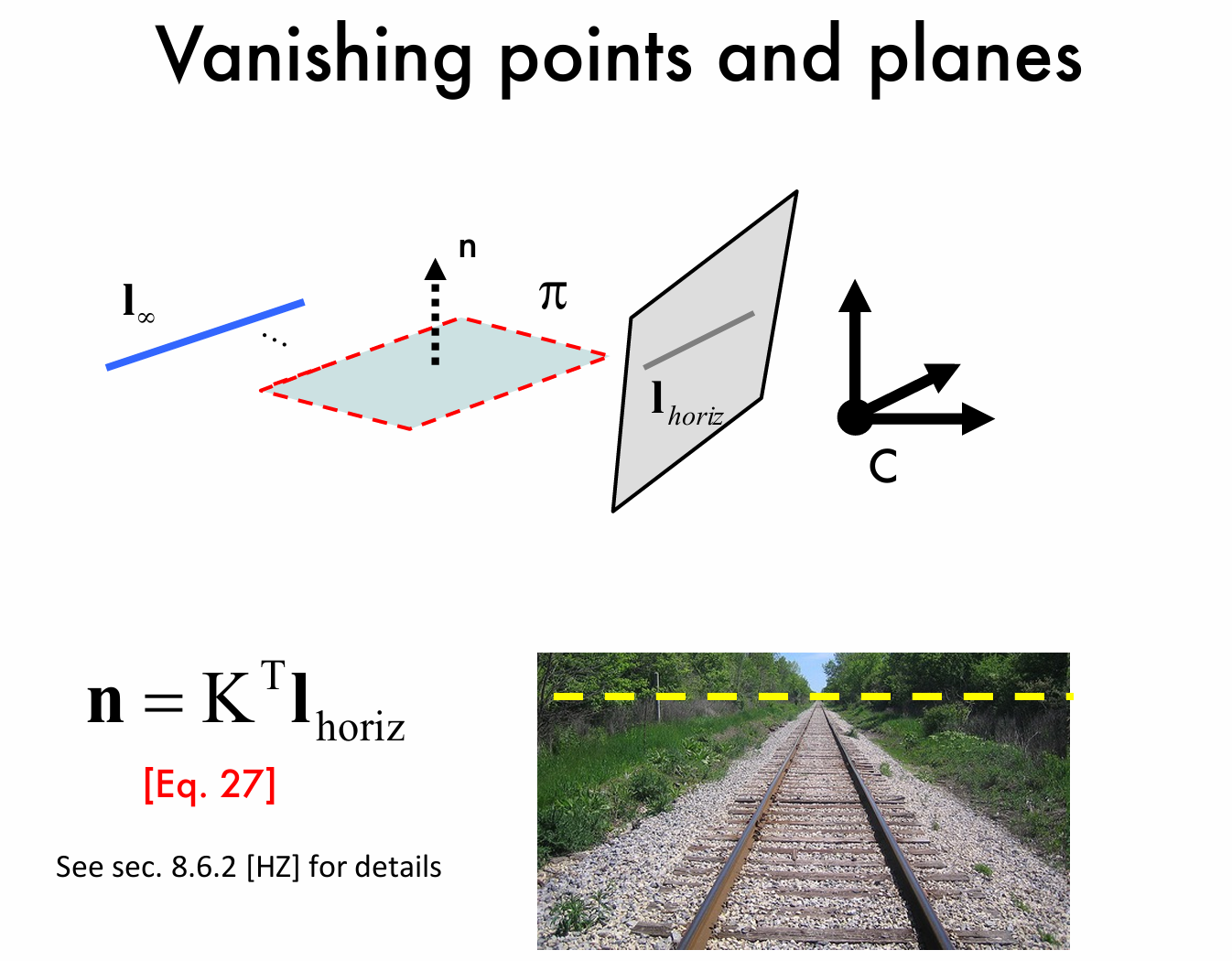
在我们把三维世界的点变换到二维点的过程中，消影线也被称为地平线（horizon line），与二维点的计算方法类似，$l_{hor}=H_P^{-T}l_∞$，如果在一幅图像中，我们能够识别到两条直线交于地平线，那么在真实的三维世界中，这两条直线就是平行的。

通过地平线，我们也能求出图像平面的法向量，即 $\mathbf{n}=\mathbf{K}^T\mathbf{l}_{horiz}$。

平行平面交于无穷远线，那么无穷远线组成的集合也被定义为无穷远平面 $\Pi_∞$ 。与二维平面的无穷远线类似，无穷远平面 $\Pi_∞=\begin{bmatrix}0\\ 0 \\0 \\ 1\end{bmatrix}$ 。

如果我们有两个直线的方向向量，那么我们就能得到他们对应的消影点，现在我们希望知道这两个点之间的角度关系。如下图，我们得出了下述公式：

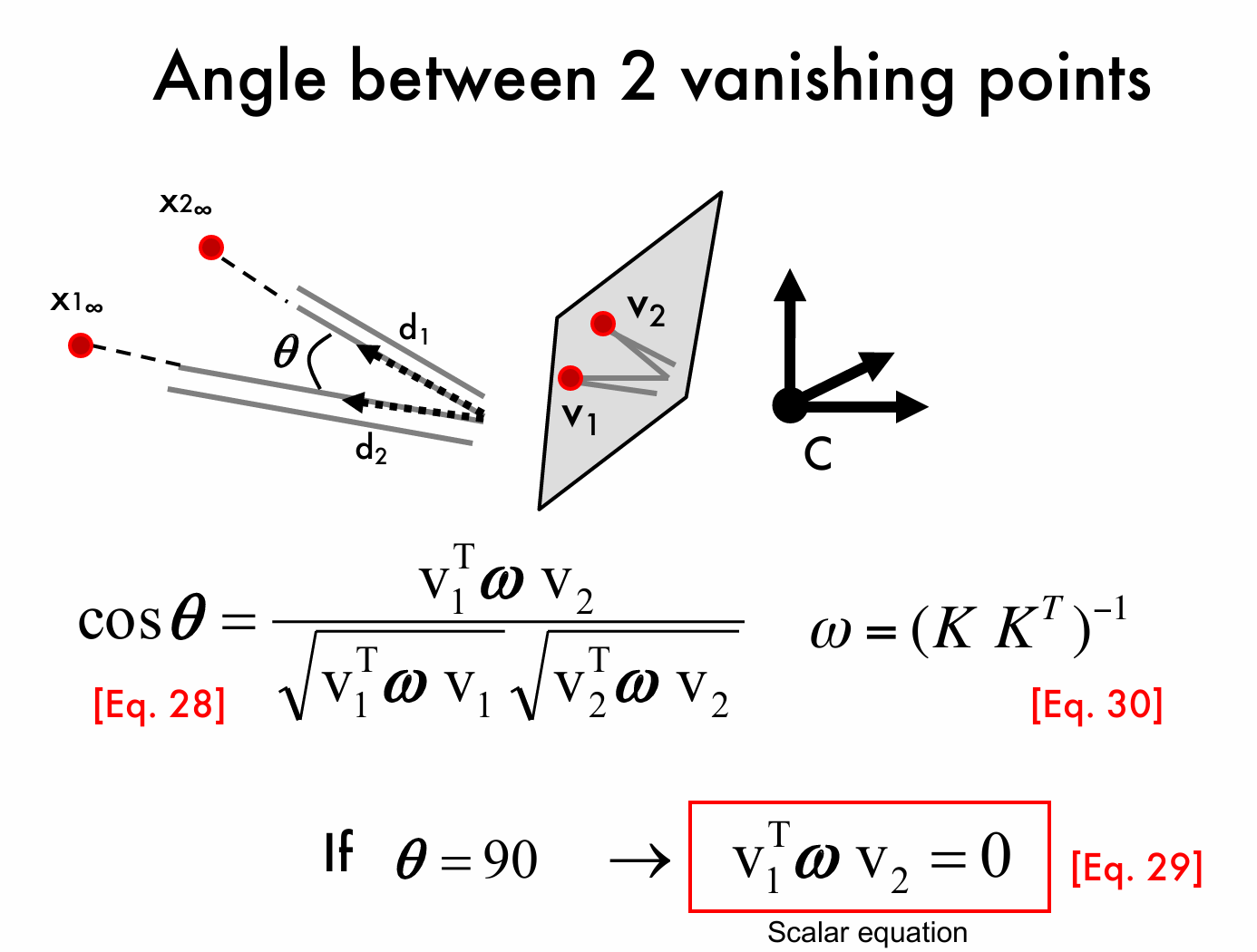
这里我们引入了一个 $w$ 矩阵，它被称为相机对偶协方差矩阵，具有一些特殊的性质：

性质1：$\omega$ 可展开为 $\omega=\begin{bmatrix}\omega_1 & \omega_2 & \omega_4 \\ \omega_2 & \omega_3 & \omega_5 \\ \omega_4 & \omega_5 & \omega_6\end{bmatrix}$ ，它是对称矩阵，并且在一定尺度下是已知的。
性质2：当 $\omega_2 = 0$ 时，表示零倾斜，即图像像素之间不存在倾斜关系。
性质3：当 $\omega_2 = 0$ 且 $\omega_1 = \omega_3$ 时，表示像素为正方形，意味着图像在水平和垂直方向上的像素尺度相同。

最后我们总结一下：

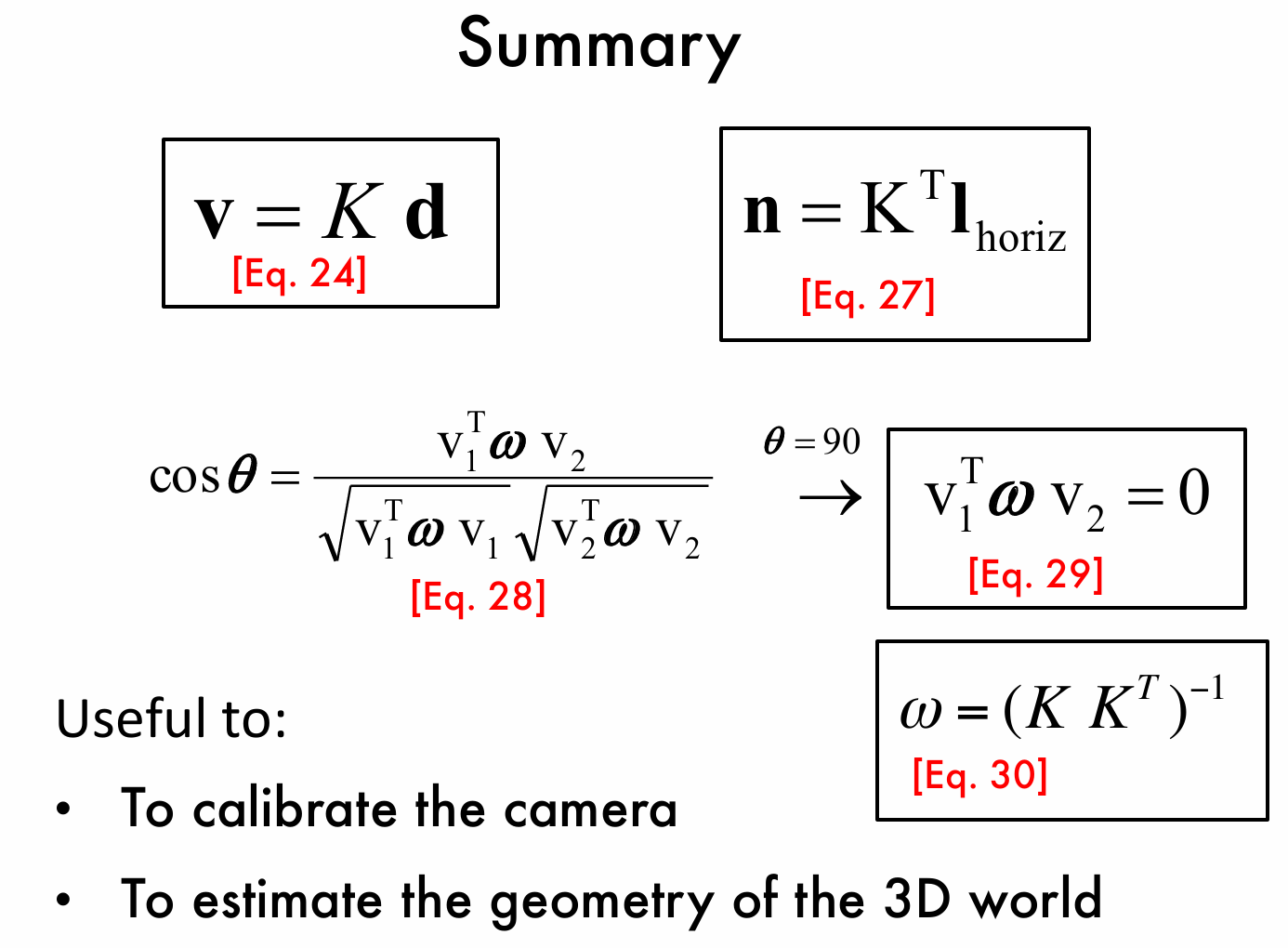
利用这些信息，我们可以更好地去标定相机或者估计三维世界的几何形态。

从单视图估计几何图形（Estimating geometry from a single image）

如果我们知道消影点的角度关系，特别地这里我们选取正交的消影点，则我们有 $v_1^Twv_2=0$，而我们又有 $w=(KK^T)^{-1}$ ，那我们能否估计出相机的内参矩阵 $K$ 呢？事实上，由于 $K$ 有5个自由度，而
$v_1^Twv_2=0$ 是一个标量方程，因此仅靠此方程可能不足以估计 $K$。

事实上，如果我们选取三个两两正交的形成的消影点，那么我们就可以建立出三个方程，如图中公式31，同时由于我们前面介绍的 $w$ 矩阵的性质，我们这里认为图像是零倾斜且像素为正方形，因此我们有 $w_2=0$ 和 $w_1=w_3$，从而我们只需要求解4个未知数，但由于 $w$ 是在一定尺度下已知，意味着存在一个自由度可用于归一化，在这种特殊情况下，这3个方程理论上是足够求解的。