P1121 环状最大两段子段和

链接

https://www.luogu.com.cn/problem/P1121

题目

思路

这个O(n)的思路很好：https://www.cnblogs.com/kamimxr/p/11438701.html。 关键思路：

答案分两种情况，一种是选择的两段均不跨越n到1(也就是环)，另一种是选择的两段跨过了环;

如果均不跨越环，那么也就是意味着这是一道模板题；

设maxl[i]表示从1-i的最大字串和，maxr[i]表示i-n的最大字段和；

很明显的:答案就是max(maxl[i]+maxr[i+1])

maxl[i]=max(a[i],maxl[i-1]+a[i]);//表示这一位是不是一段区间的开头；
maxl[i]=max(maxl[i-1],maxl[i]);
maxr[i]=max(a[i],maxr[i+1]+a[i]);
maxr[i]=max(maxr[i],maxr[i+1]);

然后处理环：
我们换种思维，就好比并查集维护联通时可以运用逆向思维一样，把拆边改为加边，你求1~n带环的最大值就等价于求(1-n的区间和)减去(1-n的两段区间最小值)
补充一个解释：

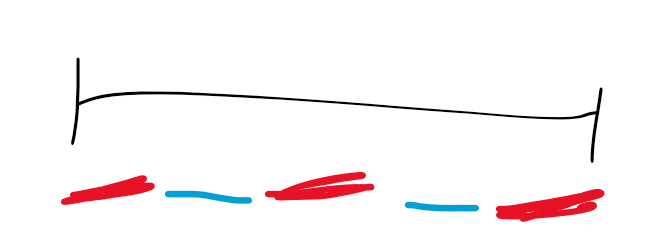
红色是跨端点连接成一段,那么最终形成的另外两段就只需要求最小值就行了。

代码

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<queue>
#include<cmath>
#include<map>
#include<string.h>
#include<limits.h>
#include<string>
#include<vector>
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
#define int long long 
const int N = 2e5 + 10;
int a[N];
int sumn;
int maxl[N], maxr[N], minl[N], minr[N];signed main()
{IOS;int n; cin >> n;int cnt = 0;for (int i = 0; i < n; i++){cin >> a[i]; sumn += a[i];if (a[i] > 0)cnt++;}int ans = 0;if (cnt <= 2){priority_queue<int>pq;for (int i = 0; i < n; i++)pq.push(a[i]);ans += pq.top();pq.pop();ans += pq.top();pq.pop();}else{//注意这里一定要分开求max!!分两步,第一步决定是否是这个数开头,第二步才是对历史信息的综合。如果过早求max会丢失信息for (int i = 0; i < n; i++){if (i == 0)maxl[i] = a[i], minl[i] = a[i];else maxl[i] = max(a[i],  maxl[i - 1] + a[i]), minl[i] = min(a[i],  minl[i - 1] + a[i]);}for (int i = 1; i < n; i++){maxl[i] = max(maxl[i], maxl[i - 1]), minl[i] =  min(minl[i - 1], minl[i] );}for (int i = n - 1; i >= 0; i--){if (i == n - 1)maxr[i] =a[i], minr[i] =a[i];else maxr[i] = max(a[i],maxr[i + 1] + a[i]), minr[i] = min(a[i], minr[i + 1] + a[i]);}for (int i = n - 2; i >= 0; i--){maxr[i] =max(maxr[i + 1], maxr[i]), minr[i] =min(minr[i + 1], minr[i]);}int ansmax = 0, ansmin = LLONG_MAX;for (int i = 0; i + 1 < n; i++)ansmax = max(ansmax,maxl[i] + maxr[i + 1]),ansmin = min(ansmin,minl[i] + minr[i + 1]);ans = ansmax;if (ansmin != LLONG_MAX and sumn - ansmin > ans)ans = sumn - ansmin;}cout << ans;return 0;
}