简述
我们有这样一个问题:修改点权,询问链上的点权和。这明显是个树链剖分模版。
但如果还有这些操作呢:断开一条边,连上一条边,保证一直是森林。这就是动态树的一种问题。
而 LCT 就是解决这些问题的优秀数据结构。
前言
建议是会 Splay,虽然 FHQ-Treap 也能写,但是多一个 \(\log\)。
Splay 只要会一些简单的序列操作和打懒标记就好了。
点进来的都会树剖会吧,不会的话也行。
Splay 表示树,splay 表示伸展操作。
动态树不是 LCT,LCT 是解决动态树问题的数据结构。
实现
实链剖分
在树剖中,最常用的是重链剖分。
而在动态树中,问题的瓶颈变成了怎么让树链的划分状况随树的形态快速修改。
但是,\(size\) 显然是难以维护的。
那么只要没有规则,不就可以快速修改了吗?
我们让每个节点的重儿子自己选择,这样在改变树形态的时候可以更自由地维护树链的变化。
这就是实链剖分。
我们选择在一条链上的边叫实边,链接不同链的边叫虚边。
节点用实边链接的是实儿子,其余是虚儿子。
每个节点至多有一个实儿子。
实链剖分和重链剖分的区别在于:一条链不一定会链接到叶子节点。
辅助树
现在,这棵树这我们分成了若干实链,现在,我们就需要辅助树维护这些链。而这棵辅助树往往是 Splay。
显然辅助树上的节点和原树上的节点一一对应。
我们还需要在辅助树上的中序遍历就是一条实链。
那么,我们怎么将原树的虚实链对应到辅助树上呢?
我们在 Splay 记录了儿子和父亲两个信息。
那么记录链上的每个点的父亲。
但是对于虚链,不记录其父亲的儿子信息,即认父不认子。
对于实链,我们需要修改其父亲的儿子。
每个 Splay 的根是一条实链的顶点,而根也有可能有父亲节点。
显然一棵树的辅助树的形态不止一种。
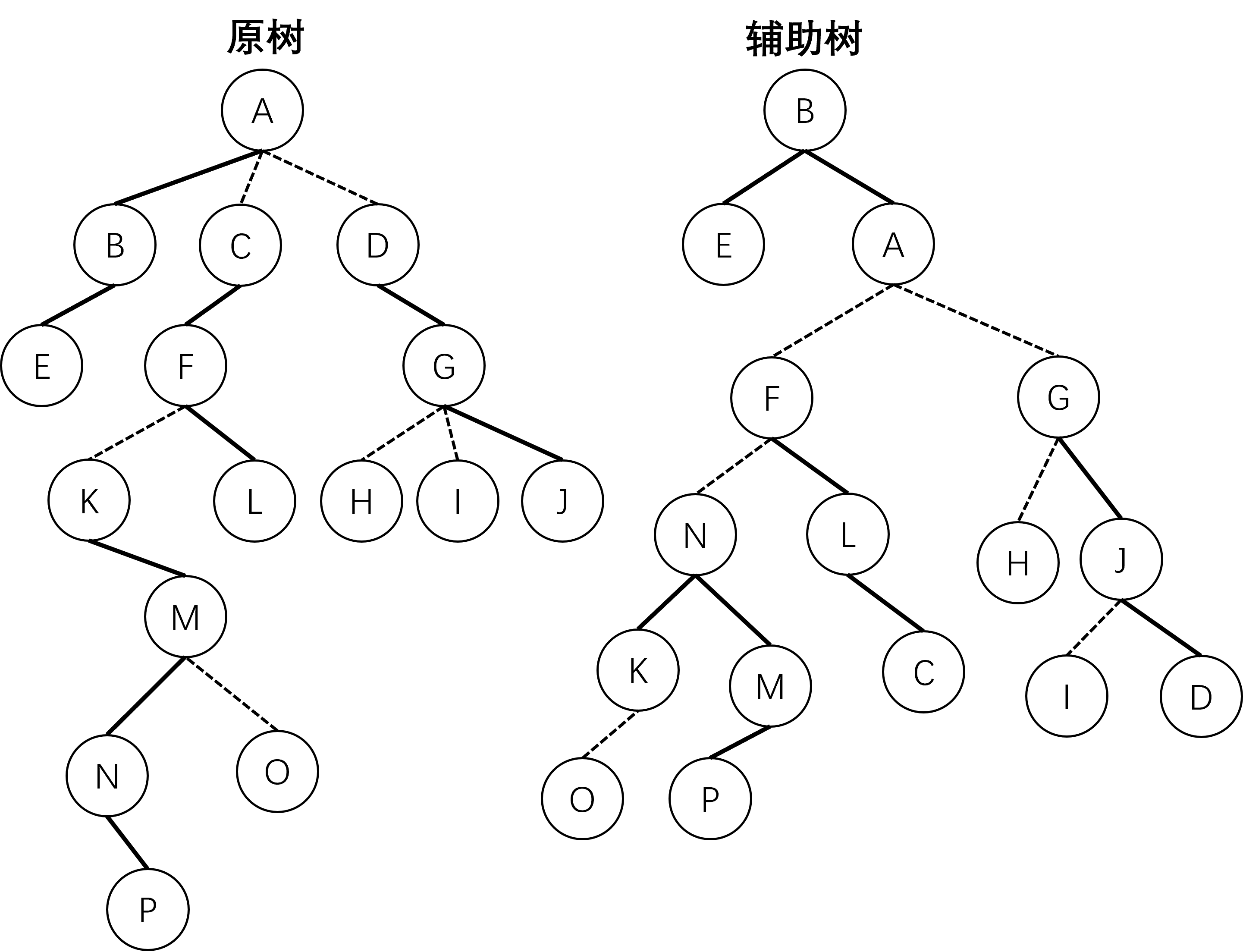
那么我们得到了辅助树和原树之间的关系:
- 一棵 Splay 表示一条实链。
- 原树的虚边,由儿子所在 Splay 的根节点指向该点,但该点不指向虚儿子。
- Splay 上虽然至多只有两个实儿子,但虚边可以有很多条。
- 原树的根不等于辅助树的根,辅助树在不破坏 Splay 性质的情况下可以随意换根。
- 原树的 father 指向和辅助树不同,注意区分。
在辅助树上,更易于进行虚实链之间的变换,这一点会在后文进行讲解。
Splay 的操作
知道了实链剖分和辅助树的概念,就可以开始实现 LCT 的一些常用函数了。
get
判断 \(x\) 是它父亲的哪个儿子。
#define get(x) (rs(fa(x)) == x)
isroot
LCT 新增函数,判断 \(x\) 是否为这棵 Splay 的根。
根据虚边认父不认子的性质,如果 \(x\) 父亲的两个儿子都找不到它,那么 \(x\) 是 Splay 的根。
#define isroot(x) (rs(fa(x)) != x && ls(fa(x)) != x)
pushup
根据题目进行维护。
pushdown
LCT 绝大部分时候都要在 Splay 上维护区间翻转标记。
其他的根据题目实现,这里展示区间翻转的实现
翻转标记有两种不同含义:
- 表示打标记的节点没有更改过,例如没有换过左右儿子。
- 表示打标记的节点已经更改好了,例如左右儿子已经调换过。
两种写法没有什么本质区别,但在后面一些地方 pushdown 的顺序写起来不一样。
第一种写法大多时候代码更简单,但有些题,维护的信息与左右儿子的顺序有关,这个时候只能用第二种写法。
第一种:
void pushdown(int x){if(!d[x].rev)return;swap(ls(x), swap(rs(x))), d[ls(x)].rev ^= 1, d[rs(x)].rev ^= 1, d[x].rev = 0;
}
第二种
void change(int x){d[x].rev ^= 1, swap(ls(x), rs(x));}
void pushdown(int x){if(d[x].rev)change(ls(x)), change(rs(x)), d[x].rev = 0;
}
alldown
之前进行区间修改的时候,需要查排名,会将从根到 \(x\) 路径上的懒标记下放。
但 LCT 不关心排名,我们就需要 alldown 函数来下放。
//递归
void alldown(int x){if(!isroot(x))alldown(fa(x));pushdown(x);
}
//栈
void alldown(int x){int stk[N], top = 0;do stk[++top] = x, x = fa(x) while(!isroot(x));while(top--)pushdown(stk[top + 1]);
}
rotate
rotate 与原义相同,把 \(x\) 向上旋转一层。
由于我们要判断 \(y\) 是否是根,不能再简单判断 \(z\) 是否是 \(0\)。
且 \(y\) 和父亲的连边断开再判断失效,所以我们把这句话提到前面。
void rotate(int x){int y = fa(x), z = fa(y), c = get(x);if(!isroot(y))d[z].ch[get(y)] = x;fa(d[y].ch[c] = d[x].ch[!c]) = y, fa(fa(d[x].ch[!c] = y) = x) = z;pushup(y), pushup(x);
}
Splay
把判断是否为根的语句换成 isroot 即可。注意 Splay 之前要先 alldown 这条路径。
void splay(int x){for(int f = fa((alldown(x), x));f = fa(x), !isroot(x);rotate(x))if(!isroot(f))rotate(get(f) ^ get(x) ? x : f);
}
汇总
Splay 部分代码
struct node{int rev, size, ch[2], fa, s, val;
}d[N];
#define ls(x) d[x].ch[0]
#define rs(x) d[x].ch[1]
#define fa(x) d[x].fa
#define get(x) (rs(fa(x)) == x)
#define isroot(x) (rs(fa(x)) != x && ls(fa(x)) != x)
void pushup(int x){d[x].s = d[ls(x)].s + d[rs(x)].s + d[x].val;}
void change(int x){d[x].rev ^= 1, swap(ls(x), rs(x));}
void pushdown(int x){if(d[x].rev)change(ls(x)), change(rs(x)), d[x].rev = 0;}
void alldown(int x){if(!isroot(x))alldown(fa(x));pushdown(x);
}
void rotate(int x){int y = fa(x), z = fa(y), c = get(x);if(!isroot(y))d[z].ch[get(y)] = x;fa(d[y].ch[c] = d[x].ch[!c]) = y, fa(fa(d[x].ch[!c] = y) = x) = z;pushup(y), pushup(x);
}
void splay(int x){for(int f = fa((update(x), x));f = fa(x), !isroot(x);rotate(x))if(!isroot(f))rotate(get(f) ^ get(x) ? x : f);
}
新的操作
access
access(x) 的作用是把 \(x\) 到根的路径上的点放进一棵 Splay 里,且这棵 Splay 里没有这条路径以外的点。
LCT 的所有函数都需要 access 操作。
左边是 access(N) 后的原树,右边是辅助树的更改过程。
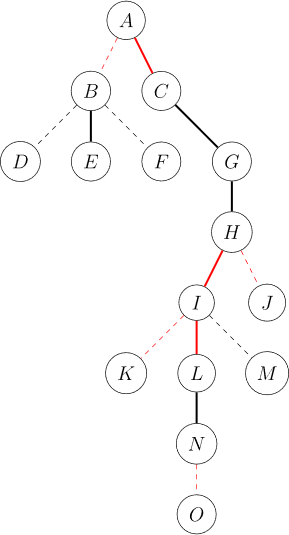
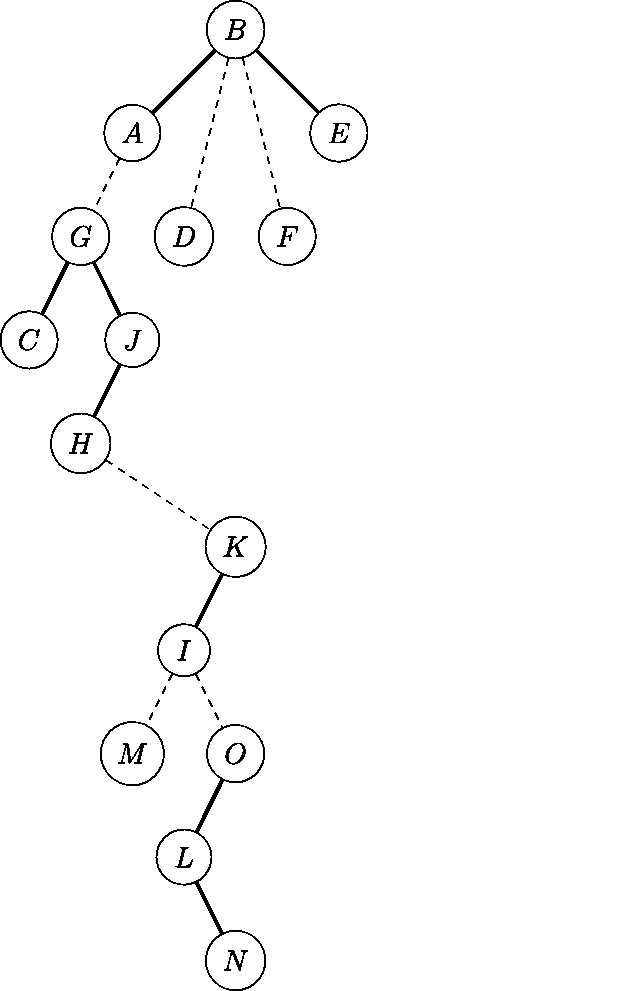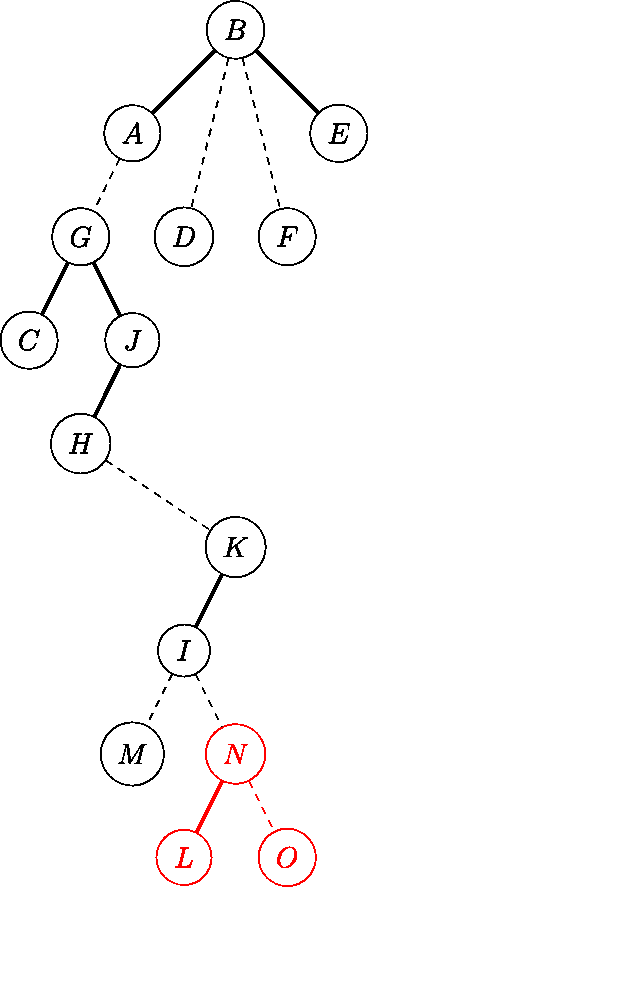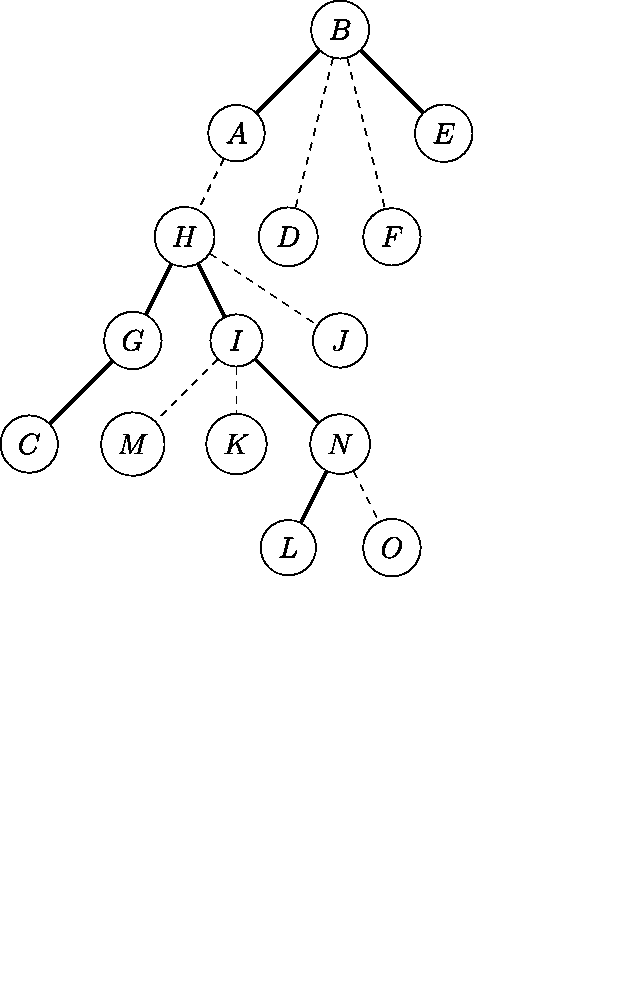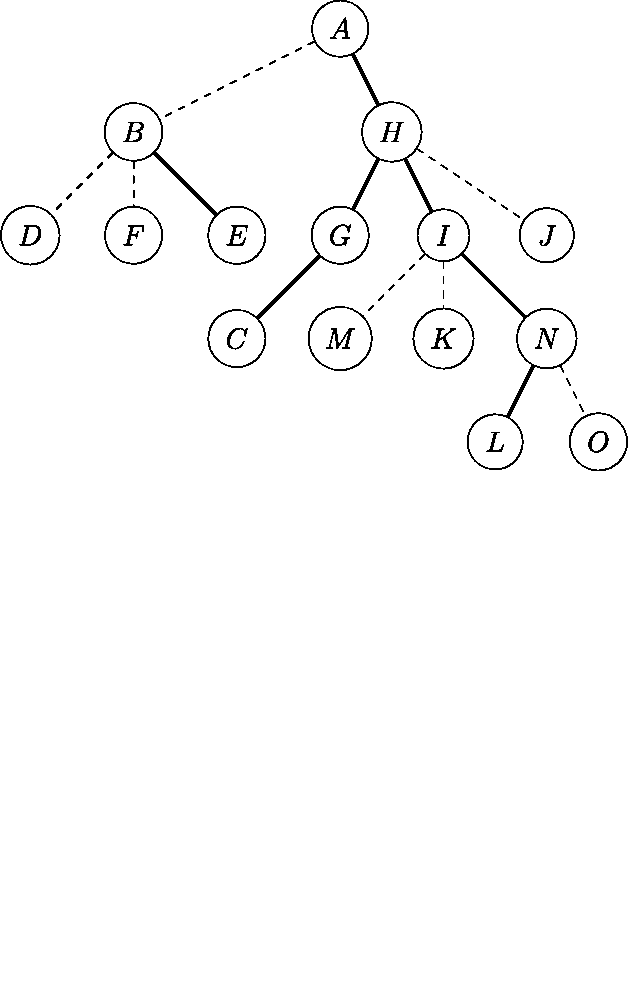
我们整理一下过程。
- 把当前节点 splay 到根;
- 令它的右儿子等于上次旋转的节点,并 pushup。
- 跳到当前点的父亲,重复以上步骤。
int access(int x){int s = 0;for(; x; s = x, x = fa(x))splay(x), rs(x) = s, pushup(x);return s;
}
这里我们返回了最后一次虚实链变换时虚边父亲节点的编号。该值有两个含义:
- 连续两次
access操作时,第二次操作的返回值等于这两个节点的 LCA. - 表示 \(x\) 所在的 Splay 树的根,且父亲一定为空。
makeroot
在维护一个路径信息时,往往路径是先向上再向下的,这样的路径无法出现在同一棵 Splay 里。
但是我们还想维护它的信息,怎么办呢?
我们可以把原树的根换掉!makeroot(x) 的作用就是把 \(x\) 换成原树的根。
那我们先 access(x),把 \(x\) 到 \(rt\) 弄到一棵 Splay 上,然后 splay(x) 一下。
但是 Splay 里的点是按中序遍历存的,设原来的原树根是 \(rt\) ,考虑换成 \(x\) 会对哪些点的上下顺序产生影响:
只有 \(x\) 到 \(rt\) 这条路径上的点上下顺序反过来了。也就是把这一段的 Splay 区间翻转。
void makeroot(int x){access(x), splay(x), change(x);}
find
find(x) 的作用是查找 \(x\) 所在原树的根。
我们知道,access(x) 也是把 \(x\) 到原树的根这一段变成实链。
那么先 access(x),再 splay(x),以 \(x\) 为根的这个 Splay 就表示从原树的根到 \(x\) 的实链。
根据 Splay 的性质,原树的根是这条链从上到下第一个点,也就是这棵 Splay 中序遍历里的第一个点。
Splay 中序遍历里的第一个点,不难发现就是 \(x\) 一直往左儿子走,直到没有左儿子,这个点就是原树的根。
注意懒标记和判断先后顺序表示。
找到根后要 splay(x) 来保证复杂度。
int find(int x){access(x), splay(x);while(ls(x))pushdown(x), x = ls(x);return splay(x), x;
}
split
split(x, y) 的作用是把 \(x\) 到 \(y\) 的路径变成一棵 Splay。
我们先 makeroot(x) 接下来执行 access(y),就找到了这条路径。
还有个问题是这样不知道 Splay 的根,所以后面一般会再做一步 splay(y)。
void split(int x,int y) {makeroot(x),access(y),splay(y);}
link
link(x,y) 表示给 \(x\) 和 \(y\) 之间连一条边。
那么我们先 makeroot(x),让 \(x\) 成为自己这棵树的根,然后判断它们两个是否已经连通。
如果不连通,直接把点 \(x\) 作为虚儿子单向指向 \(y\) 即可。
void link(int x, int y){makeroot(x);if(find(y) != x)fa(x) = y;}
cut
cut(x, y) 表示把 \(x\) 和 \(y\) 的边断开。
我们先 Split(x, y),这时候 y 是根,x 一定是它的儿子,双向断开即可。
不过还要判是否有边,我们发现,它们右边当且仅当:
- \(x\) 和 \(y\) 连通。
- \(x\) 到 \(y\) 的路径之间没有其他点。
由于 Splay 是中序排序,且 \(y\) 是根,那么他们有边仅当 \(x\) 的父亲是 \(y\),且 \(x\) 没左儿子。
void cut(int x, int y){split(x, y);if(fa(x) == y && !ls(x))fa(x) = ls(y) = 0;}
时间复杂度
为均摊 \(\log(n)\)。
证明
来源 oi.wiki。
LCT 中的大部分操作都基于 access,其余操作的时间复杂度都为常数,因此我们只需要分析 access 操作的时间复杂度。
其中,access 的时间复杂度主要来自于多次 splay 操作和对路径中虚边的访问,接下来分别分析这两部分的时间复杂度。
- splay
- 定义 \(w(x) = \log size(x)\),其中 \(size(x)\) 表示以 \(x\) 为根的所有虚边和实边的数量之和。
- 定义势能函数 \(\Phi = \sum_{x \in T} w(x)\),其中 \(T\) 表示所有节点的集合。
- 由 Splay 的时间复杂度 分析易知,splay 操作的均摊时间复杂度为 \(O(\log n)\)。
- 访问虚边
定义两种虚边:
- 重虚边:从节点 \(v\) 到其父节点的虚边,其中 \(size(v) > \frac{1}{2} size(parent(v))\)。
- 轻虚边:从节点 v 到其父节点的虚边,其中 \(size(v) \leq \frac{1}{2} size(parent(v))\)。
对于虚边的处理,可以使用势能分析,定义势能函数 \(\Phi\) 为所有重虚边的数量,定义均摊成本 \(c_i = t_i + \Delta \Phi_i\),其中 \(t_i\) 为实际操作的成本,\(\Delta \Phi_i\) 为势能的变化。
-
走过重虚边后,会将重虚边转换为实边,该操作会减少 \(1\) 的势能,因为它通过加强重要连接来优化树的结构。且由于其实际操作成本为 \(O(1)\),抵消了势能的增加,故不会增加均摊成本,所有的均摊成本集中在轻虚边的处理上。
-
每次
access操作最多遍历 \(O(\log n)\) 条轻虚边,因此至多消耗 \(O(\log n)\) 的实际操作成本,转化得到 \(O(\log n)\) 条重虚边,即势能以 \(O(\log n)\) 的代价增加。 -
由此,最终访问虚边的均摊复杂度为实际操作成本和势能变化的和,即 \(O(\log n)\)。
综上所述,LCT 中 access 操作的时间复杂度是 splay 和 虚边访问的复杂度之和,因此最后的均摊复杂度为 \(O(\log n)\),即 n 个节点的 LCT,做 m 次 access 操作的时间复杂度为 \(O(n \log n + m \log n)\),从而 LCT 操作的均摊复杂度也为 \(O(\log n)\)。