20250221

T1

穿越

考虑从叶子向上贪心，每个点实际上可以选择一个子树中的点扩展完上来，再选择一个子树中的点下去。所以每个点开一个可并堆维护这个点的所有决策，然后每个点先把儿子的合并上来再选两个最优的决策去做。实际上 set 启发式合并也可以过。

代码

#include <iostream>
#include <set>
#define int long long
using namespace std;
int n;
int a[300005];
int head[300005], nxt[600005], to[600005], ecnt;
inline void add(int u, int v) { to[++ecnt] = v, nxt[ecnt] = head[u], head[u] = ecnt; }
multiset<pair<int, int>, greater<pair<int, int> > > st[300005];
int f[300005];
void Merge(multiset<pair<int, int>, greater<pair<int, int> > > &a, multiset<pair<int, int>, greater<pair<int, int> > > &b) {if (a.size() > b.size()) swap(a, b);for (auto v : a) b.insert(v);
}
void dfs(int x, int fa) {int cs = 0;for (int i = head[x]; i; i = nxt[i]) {int v = to[i];if (v != fa) {++cs;dfs(v, x);st[x].insert(make_pair(f[v], v));}}for (int i = 1; i <= 2 && st[x].size(); i++) {pair<int, int> p = *st[x].begin();f[x] += p.first;st[x].erase(st[x].begin());Merge(st[p.second], st[x]);}f[x] += a[x];
}
signed main() {freopen("travel.in", "r", stdin);freopen("travel.out", "w", stdout);cin >> n;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i < n; i++) {int u, v;cin >> u >> v;++u, ++v;add(u, v);add(v, u);}dfs(1, 0);cout << f[1] << "\n";return 0;
}

T2

树上水题

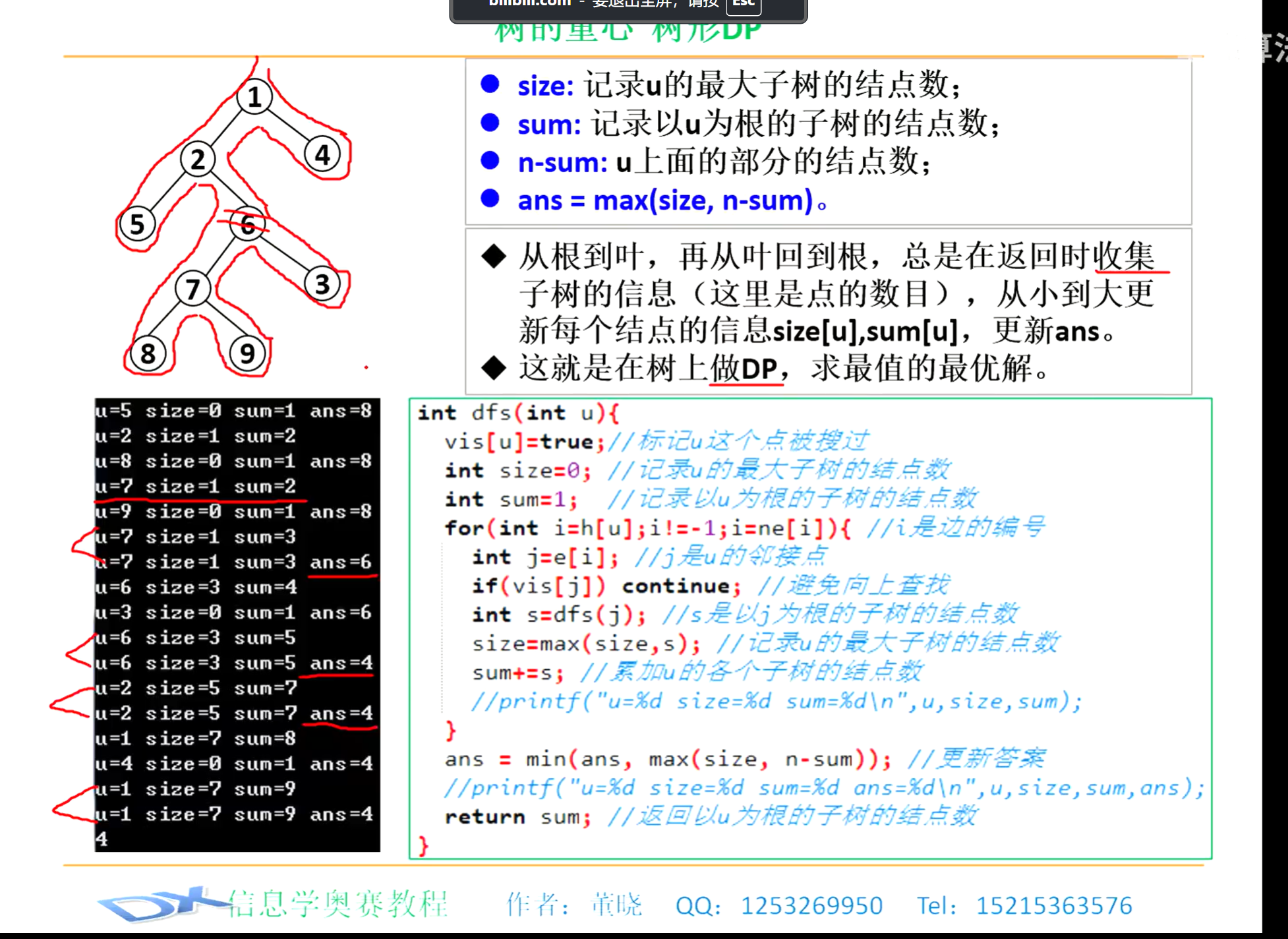
考虑如果只能选子树，则容易 \(n^2\) 做。希望尽量简单一点，可以选取重心作为根，这样如果点集的 LCA 不是根，则选的就一定是子树而不是外子树。于是只需要考虑点集的 LCA 不为根的情况，这个时候选的一定是整棵树去掉根的一棵子树形成的连通块。考虑对于每个 \(x\) 计算答案 \(\ge x\) 的方案数，答案就是所有方案数加起来。如果答案 \(\ge x\)，则所有子树大小 \(\ge n - x + 1\) 的子树当中都至少需要选择一个点。考虑所有符合要求的极小子树，这些子树两两不交。我们考虑对着这个东西容斥，钦定一些极小子树不选。设所有极小子树的大小构成多重集 \(A\)，则答案 \(ans = \sum\limits_{S \subseteq A}(-1)^{|S|}\binom{n - \sum\limits_{x \in A} x}{k}\)。考虑对于每个上面那个东西求出容斥系数的总和，然后对于每个 \(k\) 统一算答案。这个容易背包求出。然后随着 \(x\) 的增加，\(A\) 里东西的变化总次数是 \(\mathcal{O}(n)\) 级别，可以直接暴力更新背包。于是做完了，总复杂度 \(\mathcal{O}(n^2)\)。

代码

#include <iostream>
#include <vector>
#include <array>
#define int long long
using namespace std;
const int P = 998244353;
inline void Madd(int &x, int y) { (x += y) >= P ? (x -= P) : 0; }
int fac[20005], ifac[20005], inv[20005];
void Cpre(int n) {fac[0] = fac[1] = ifac[0] = ifac[1] = inv[0] = inv[1] = 1;for (int i = 2; i <= n; i++) {fac[i] = fac[i - 1] * i % P;inv[i] = (P - P / i) * inv[P % i] % P;ifac[i] = ifac[i - 1] * inv[i] % P;}
}
inline int C(int n, int m) { return (n < 0 || m < 0 || n < m) ? 0 : fac[n] * ifac[m] % P * ifac[n - m] % P; }
int qpow(int x, int y = P - 2) {int ret = 1;while (y) {if (y & 1) ret = ret * x % P;y >>= 1;x = x * x % P;}return ret;
}
int n;
int head[7005], nxt[20005], to[20005], ecnt;
inline void add(int u, int v) { to[++ecnt] = v, nxt[ecnt] = head[u], head[u] = ecnt; }
int rt, msz;
int sz[7005], mx[7005];
void getroot(int x, int fa) {sz[x] = 1;for (int i = head[x]; i; i = nxt[i]) {int v = to[i];if (v != fa) {getroot(v, x);sz[x] += sz[v];mx[x] = max(mx[x], sz[v]);}}   mx[x] = max(mx[x], n - sz[x]);if (mx[x] < msz) msz = mx[x], rt = x;
}
int fa[7005];
vector<array<int, 2> > vec[7005];
void dfs(int x, int fa) {mx[x] = 0, sz[x] = 1; ::fa[x] = fa;for (int i = head[x]; i; i = nxt[i]) {int v = to[i];if (v != fa) {dfs(v, x);sz[x] += sz[v];mx[x] = max(mx[x], sz[v]);}}if (x != rt) {vec[sz[x]].emplace_back((array<int, 2>) { sz[x], 1 });vec[mx[x]].emplace_back((array<int, 2>) { sz[x], 0 });}
}
int cur[7005], coe[7005], ans[7005];
void ins(int x) { for (int i = 1; i <= n - x; i++) Madd(cur[i], P - cur[i + x]); }
void del(int x) { for (int i = n; i > x; i--) Madd(cur[i - x], cur[i]); }
signed main() {freopen("tree.in", "r", stdin);freopen("tree.out", "w", stdout);Cpre(7000);cin >> n;for (int i = 1; i < n; i++) {int u, v;cin >> u >> v;add(u, v);add(v, u);}msz = n + 1;getroot(1, 0);dfs(rt, 0);for (int i = 1; i <= n; i++) {if (i == rt) continue;for (int K = 1; K <= n; K++) {int k = sz[i];Madd(ans[K], k * C(sz[i], K) % P);for (int j = head[i]; j; j = nxt[j]) {int v = to[j];if (fa[v] == i) Madd(ans[K], P - k * C(sz[v], K) % P);}}}int mx1 = 0, mx2 = 0;cur[n] = 1;for (int i = head[rt]; i; i = nxt[i]) {int v = to[i];Madd(cur[sz[v]], P - 1);if (sz[v] >= mx1) mx2 = mx1, mx1 = sz[v];else mx2 = max(mx2, sz[v]);}for (int i = 1; i <= n; i++) Madd(coe[i], (n - mx[rt]) * cur[i] % P);for (int i = 1; i < n; i++) cur[i] = 0;vec[mx1].emplace_back((array<int, 2>) { n - mx1, 1 });vec[mx2].emplace_back((array<int, 2>) { n - mx1, 0 });for (int i = mx[rt]; i; i--) {for (auto v : vec[i]) v[1] ? ins(v[0]) : del(v[0]);for (int j = 1; j <= n; j++) Madd(coe[j], cur[j]);}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) Madd(ans[i], coe[j] * C(j, i) % P);}for (int i = 1; i <= n; i++) cout << ans[i] * qpow(C(n, i)) % P << "\n";return 0;
}