- 证明向量u可以分解为任意两个向量α、向量β。即:u = s*α + t*β
-
$\begin{aligned}&. 结论:行列式D= \begin{pmatrix} a \ \ b \\ c \ \ d \end{pmatrix} \textcolor{red}{不为零}时才能被分解 \\ & 证明 : 设向量\vec{V},当行列式D=(ad-bc)不为零时,才存在实数s、t,使得\vec{V} = s*\vec{v_1} + t*\vec{v_2}成立 \\ \end{aligned}
$
$ \begin{aligned}\ \ \ 证: \\ \ \ \ \ \ \ \vec{V} &= s*\vec{v_1} + t*\vec{v_2} \\ \ \ \ \ \ \ \vec{V} \times (\vec{v_1}) &= (s*\vec{v_1} + t*\vec{v_2}) \times (\vec{v_1}) \ \ \ \ \ \ \ \ \ \ \ \ & ① 两边同时叉乘\vec{v_1} \\ \ \ \ \ \ \ &= [(s*\vec{v_1}) \times \vec{v_1}] + [(t*\vec{v_2}) \times \vec{v_1}] \ \ \ \ \ \ \ \ \ \ \ \ & ② \textcolor{red}{分配律}\\ \ \ \ \ \ \ &= \textcolor{green}{0} + [(t*\vec{v_2}) \times \vec{v_1}] \ \ \ \ \ \ \ \ \ \ \ \ & ③ \textcolor{green}{前半部分为0}:自己叉乘自己,平行四边形面积为零\\ \ \ \ \ \ \ &= 0 + \textcolor{red}{[t*(\vec{v_2}\times \vec{v_1})]} \ \ \ \ \ \ \ \ \ \ \ \ & ④ \textcolor{red}{后半部分括号交换}:带入公式叉乘=平行四边形面积=\vec{v_1}*\vec{v_2}*sinθ发现是对的\\ \ \ \ \ \ \ \frac{\vec{V} \times (\vec{v_1}) }{(\vec{v_2}\times \vec{v_1})} &= t \ \ \ \ \ \ \ \ \ \ \ & ⑤ 移项 \\ \ \ \ \ \ \ t &= \frac{\vec{V} \times (\vec{v_1}) }{ \textcolor{red}{(\vec{v_2}\times \vec{v_1})}} \ \ \ \ \ \ \ \ \ \ \ & ⑥ 上述步骤消去s,得出t受到\textcolor{red}{分母不为零}影响 \\ & & 分母是\vec{v_2} 叉乘 \vec{v_1},也就是说平行四边形\textcolor{red}{面积不为零}才成立 \\ & & 分母是\vec{v_2} 叉乘 \vec{v_1},也就是说行列式D\textcolor{red}{ \begin{pmatrix} a \ b \\ c \ d \end{pmatrix} } = (ad-bc) 不为零才成立 \\ & & 分母是\vec{v_2} 叉乘 \vec{v_1},也就是说\vec{v_2}、\vec{v_1}\textcolor{red}{不在同一直线}才成立\end{aligned} $
-
$\begin{aligned}&. 结论:行列式D= \begin{pmatrix} a \ \ b \\ c \ \ d \end{pmatrix} \textcolor{red}{不为零}时才能被分解 \\ & 证明 : 设向量\vec{V},当行列式D=(ad-bc)不为零时,才存在实数s、t,使得\vec{V} = s*\vec{v_1} + t*\vec{v_2}成立 \\ \end{aligned}
$
- 叉乘相关
- 叉乘几何意义是
平行四边形面积 - 行列式D是一个数,二维时是平行四边形面积,三维时是体积,四维时是....
- 叉乘几何意义是
向量的一般分解证明
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/888066.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
宜家 App 存在的 bug All In One
宜家 App 存在的 bug All In One
某商品下架后,App 的订单中就无法再查看有关商品的任何详细信息宜家 App 存在的 bug All In One
bugs某商品下架后,App 的订单中就无法再查看有关商品的任何详细信息解决方案使用 Google 搜索,获取对应的商品的网页版信息https://www.ikea.c…
为 Power Automate 注册 Adobe PDF Services
前言最近,再测试如何将HTML转换成PDF,然后发现Adobe有一个免费的操作可以用,好开心,赶紧注册一下。正文1.先注册一个账号,然后登录到Adobe Developer注册链接:https://www.adobe.com/go/getstarted_powerautomate2.这就是新建好的,然后密码要获取一下,如下图:3.然后,…
记一次golang项目context引发的进程OOM故障
之前写过一篇一种基于etcd实践节点自动故障转移的思路, 程序经历过一次线上进程内存持续上涨终OOOM的小事故, 本次技术复盘导致本次内存泄露的完整起因。
提炼代码:
业务函数etcdWatchLoop: 基于etcd的Watch机制持续监听/foo前缀键值对的变更; 收到Watch信道的变更消息,就…
记一次golang项目context引发的OOM故障
之前写过一篇一种基于etcd实践节点自动故障转移的思路, 程序经历过一次线上进程内存持续上涨终OOOM的小事故, 本次技术复盘导致本次内存泄露的完整起因。
提炼代码:
业务函数etcdWatchLoop: 基于etcd的Watch机制持续监听/foo前缀键值对的变更; 收到Watch信道的变更消息,就…
R语言LCMM多维度潜在类别模型流行病学研究:LCA、MM方法分析纵向数据
全文代码数据:https://tecdat.cn/?p=39710
原文出处:拓端数据部落公众号
在数据分析领域,当我们面对一组数据时,通常会有已知的分组情况,比如不同的治疗组、性别组或种族组等。然而,数据中还可能存在未被观测到的分组,例如素食者与非素食者、经常锻炼者与不锻炼者,或…
TensorFlow域对抗训练DANN神经网络分析MNIST与Blobs数据集梯度反转层提升目标域适应能力可视化
全文链接:https://tecdat.cn/?p=39656
原文出处:拓端数据部落公众号
本文围绕基于TensorFlow实现的神经网络对抗训练域适应方法展开研究。详细介绍了梯度反转层的原理与实现,通过MNIST和Blobs等数据集进行实验,对比了不同训练方式(仅源域训练、域对抗训练等)下的分类性能…
【专题】2025年我国机器人产业发展形势展望:人形机器人量产及商业化关键挑战报告汇总PDF洞察(附原数据表)
原文链接:https://tecdat.cn/?p=39668
机器人已广泛融入我们生活的方方面面。在工业领域,它们宛如不知疲倦的工匠,精准地完成打磨、焊接等精细工作,极大提升了生产效率和产品质量;在日常生活里,它们是贴心的助手,扫地机器人默默清扫房间,陪伴机器人给予老人孩子温暖陪…
2025省选模拟13
2025省选模拟13\(T1\) P1025. Easy Problem \(40pts\)部分分\(40pts\)设 \(f_{i,j}\) 表示 \(p_{3j}=i\) 时 \([1,i]\) 对答案的贡献,状态转移方程为 \(f_{i,j}=\max\limits_{k=3(j-1)}^{i-3} \{ f_{k,j-1}+w(k+1,i) \}\) ,其中 \(w(k+1,i)\) 表示 \([k+1,i]\) 的次大值。
设…
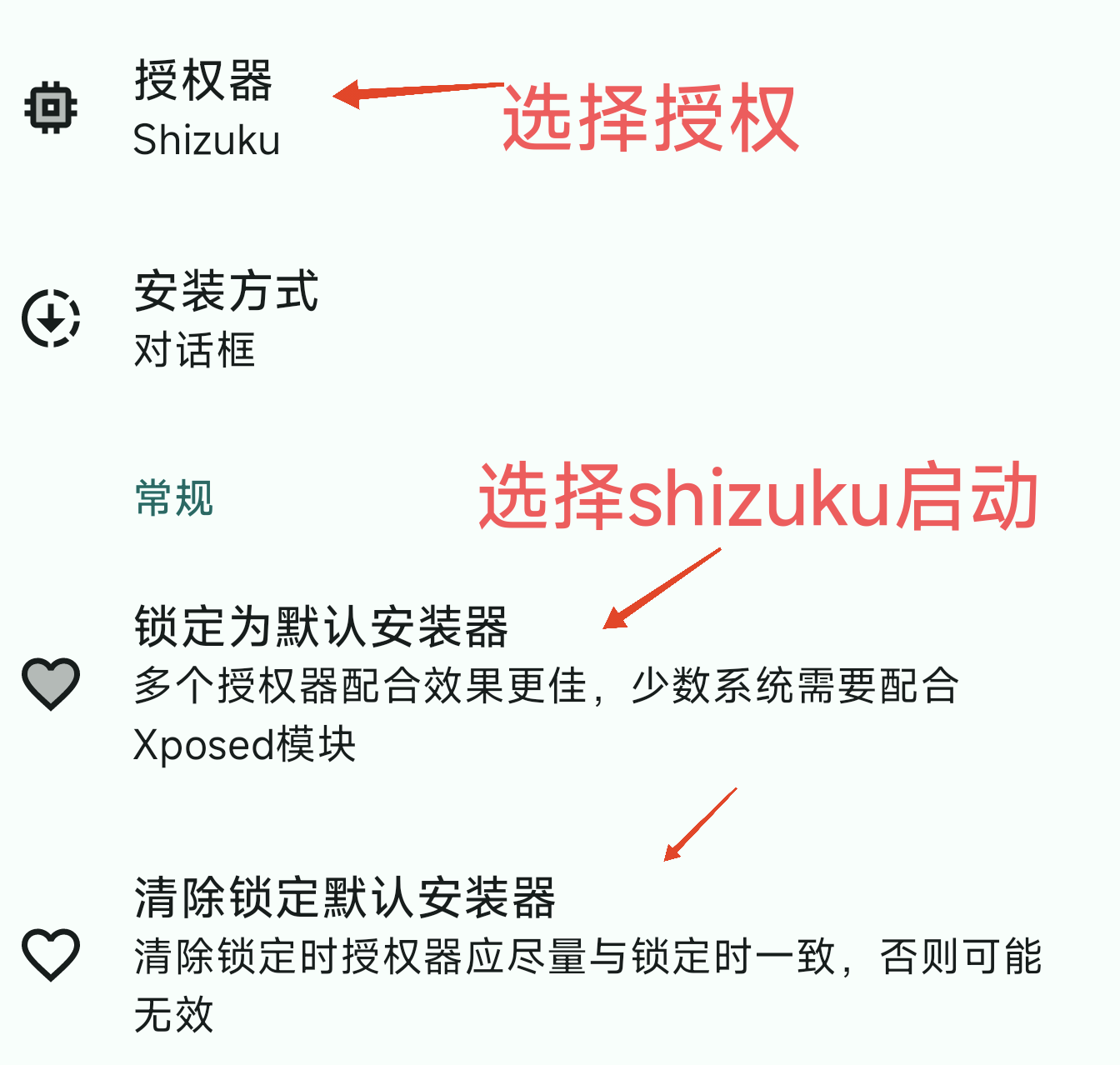
installerX还你一个清爽的安装
相信大家都有被手机自带的软件安装器折磨的情况,各种禁止安装,这种验证和识别,不开启安全模式和开了没区别,针对这种情况有没有什么办法绕过呢?
我们可以使用开源软件installerX,这款软件使用拥有这类原生的安装体验,安装速度也不差,并且简洁高效,还可以进行降级安装。…