CodeForces *2300 基准意识流做题记录

注：*2300 基准意为记录大于等于 *2300 的题目而并不仅限于等于

- CF1070J Streets and Avenues in Berhattan *2300

鉴于这题题解真的什么都没讲明白，于是我来理解一下题解在说什么。

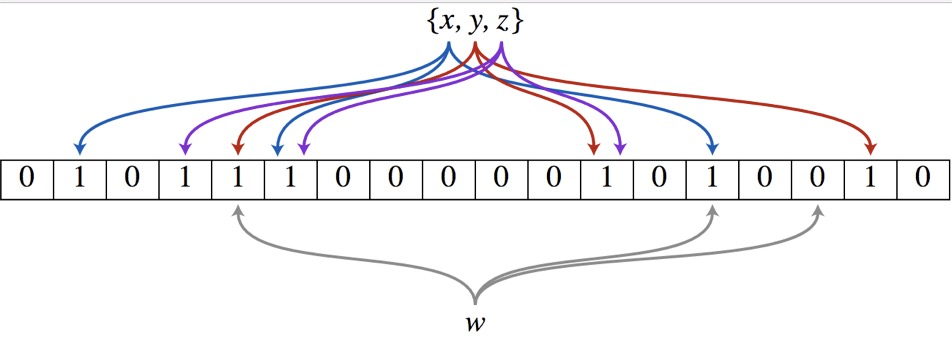
为了简化问题，我们先假设 \(n+m=k\)。比如我们给横线和竖线随机赋值，那么怎样比较优呢？根据题面，我们显然认为交叉点少优，那么就导出了我们想让同一种名字同时出现在横和竖的情况尽量的少。

我们可以猜想怎样可以满足我们这种要求，比如我们猜测让横竖都出现的名字种类数尽量少可不可行。

我们尝试证明，先考虑两项，剩下的归纳即可：

假设我们有 \(i\) 个横行 A，\(j\) 个横行 B，\(i2\) 个竖行 A，\(j2\) 个竖行 B。我们不妨设 \(i2<j\)。那么我们把 A 全放横行，其余的插空放 B。那么你稍微计算或者你瞪一下就很容易发现这个东西一定是更优的。

于是我们归纳得到强结论：只会有一个名字，使得它同时出现在横行和竖行上。

我们把这样的名字称为被标记的名字。

理解这个了之后，我们其他就好说了。我们观察这是一个什么形式，因为我们钦定了 \(n+m=k\)，所以我们竖行必定是一些整块（即这个名字全部选）拼上一些我们标记的名字，横行同理。

于是我们可以枚举横行上选了多少个我们标记的名字，其他的我们做布尔背包判定能不能拼好就行了。那么你的贡献就是 \((cnt_{flag}-j)\times j\)。

接下来我们考虑 \(n+m>k\)。基本思路是一样的。那么你考虑 \(n+m>k\) 之后，是怎样让答案减小的。其实就是你扔掉了一些被标记的名字对吧。那么我们大多数情况下还是一样，只不过可以扔掉 \(k-n-m\) 个被标记的名字。那么我们可以枚举横行的 \(j\)，然后在竖行扔掉这些点即可，反正是对称的。

所以你的贡献改为 \((cnt_{flag}-j-(k-n-m))\times j\)。注意一种特殊情况，即 \((cnt_{flag}-j-(k-n-m))<0\)，其实代表着根本不需要被标记点了（\(k\) 太大了）。这时候其实也不用管是不是整块了，答案直接是 \(0\) 就好了。

于是我们做完了。