题解 [NOISG2025 Prelim] Lasers 2

solution

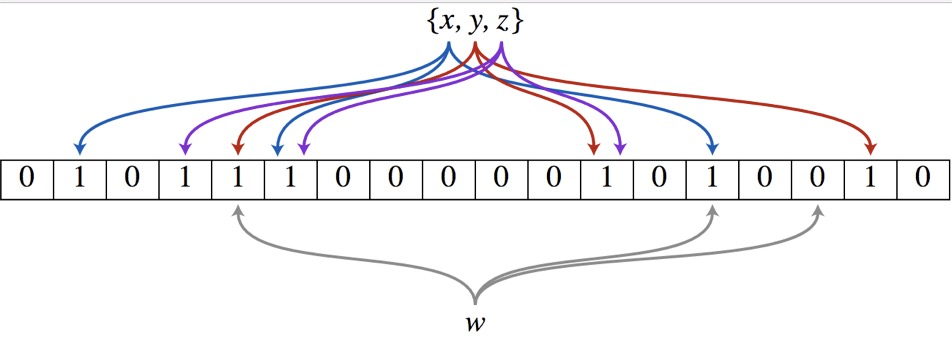
因为我们可以将所有激活墙全部放在最长的激活墙后面，而如果最长的激活墙比最长未激活墙短（也就是全场最长墙未激活），那么答案就是未激活墙的并的大小，否则我们需要找一个地方放置这个激活的全场最长墙，然后答案是未激活墙的并再并上这个最长墙的大小。

一堆区间的并还是太困难了，我们不妨按照并的连续段进行 dp。我们把问题改成最大化选中的区间的价格的和（也就是我们着眼于的是未激活的墙），先处理一个 \(sum[l,r]\) 表示所有 \(\subseteq[l, r]\) 的区间的价格，然后直接 dp，设\(f_i\) 表示考虑完 \([1, i]\) 的选择情况的最大价格，转移就 \(O(n)\) 转移。这只是一个雏形，我们还需要的是：

1. 需要有一个连续段的长度大于全场最长墙，然后再看看能不能计入全场最长墙的价格。使用一个 0/1 记录即可。
2. 需要记答案，记录有多少个空位（记作变量 \(w\)）。使用 \(O(n)\) 的时空代价即可。

此时复杂度 \(O(n^3)\)，需要优化。

发现我们将前面的 \(O(n^2)\) 个状态排成矩阵的形式，那么就是形如矩阵的某条对角线对位加上 \(sum\) 的某一列的最大值贡献到 \(f_{i, w}\)，且随着 \(i\) 增加这些对角线不会变，只有 \(sum\) 的那一列会增加。然而这样的话可以不在一开始处理 \(sum\)，而是 \(i\) 增加的时候将右端点为 \(i\) 的区间拿出来将每条对角线的某个前缀进行整体加。所以我们对每一条对角线用线段树维护即可，需要支持区间加和区间最大值（因为有一个“连续段的长度大于全场最长墙”的特殊转移需要区间最大值）。复杂度做到 \(O(n^2\log n)\) 也就是 \(O(hw\log w)\)。

code

#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#define endl "\n"
#endif
using LL = long long;
template <class T> T& chkmin(T& x, const T& y) { return x = min(x, y); }
template <class T> T& chkmax(T& x, const T& y) { return x = max(x, y); }
constexpr int N = 2010;
struct wall {int l, r, c;int length() const { return r - l + 1; }friend bool operator<(const wall& lhs, const wall& rhs) { return lhs.length() < rhs.length(); }
};
struct segtree {LL ans[N << 2], tag[N << 2];segtree() {memset(ans, ~0x3f, sizeof ans);memset(tag, 0, sizeof tag);}void spread(int p, LL k) { tag[p] += k, ans[p] += k; }void maintain(int p) { ans[p] = max(ans[p << 1], ans[p << 1 | 1]); }void pushdown(int p) { spread(p << 1, tag[p]), spread(p << 1 | 1, tag[p]), tag[p] = 0; }void setValue(int x, LL v, int p, int l, int r) {if (l == r) return ans[p] = v, void();int mid = (l + r) >> 1;pushdown(p);if (x <= mid) setValue(x, v, p << 1, l, mid);else setValue(x, v, p << 1 | 1, mid + 1, r);maintain(p);}void modify(int ql, int qr, LL k, int p, int l, int r) {if (ql <= l && r <= qr) return spread(p, k);int mid = (l + r) >> 1;pushdown(p);if (ql <= mid) modify(ql, qr, k, p << 1, l, mid);if (mid < qr) modify(ql, qr, k, p << 1 | 1, mid + 1, r);maintain(p);}LL query(int ql, int qr, int p, int l, int r) {if (ql <= l && r <= qr) return ans[p];int mid = (l + r) >> 1;pushdown(p);LL ret = -1e18;if (ql <= mid) chkmax(ret, query(ql, qr, p << 1, l, mid));if (mid < qr) chkmax(ret, query(ql, qr, p << 1 | 1, mid + 1, r));return ret;}
} tr[N][2];
int n, m;
LL lim, f[N][2][N];
vector<wall> rgs[N];
int main() {
#ifndef NFcin.tie(nullptr)->sync_with_stdio(false);
#endifcin >> m >> n >> lim, lim = -lim;wall maxw = {0, -1, 0};for (int i = 1, l, r, c; i <= m; i++) cin >> l >> r >> c, lim += c, rgs[r].push_back({l, r, c}), maxw = max(maxw, wall{l, r, c});rgs[maxw.r].push_back({maxw.l, maxw.r, -maxw.c});memset(f, ~0x3f, sizeof f);f[0][0][0] = 0;for (int i = 1; i <= n; i++) {f[i][0][0] = 0;for (int t : {0, 1}) {for (int w = 1; w <= i; w++) {auto& seg = tr[w - i + n][t];seg.setValue(i, f[i - 1][t][w - 1], 1, 1, n);for (auto wl : rgs[i]) seg.modify(1, wl.l, wl.c, 1, 1, n);chkmax(f[i][t][w], max(seg.ans[1], f[i - 1][t][w]));if (t == 0 && i >= maxw.length()) {if (maxw.r <= i) seg.modify(1, maxw.l, maxw.c, 1, 1, n);chkmax(f[i][1][w], seg.query(1, i - maxw.length() + 1, 1, 1, n));if (maxw.r <= i) seg.modify(1, maxw.l, -maxw.c, 1, 1, n);}}}}for (int i = 1; i <= n; i++) {for (int t : {0, 1}) {for (int w = 0; w <= n; w++) if (f[i][t][w] >= 0) debug("f[%d][%d][%d] = %lld\n", i, t, w, f[i][t][w]);}}for (int w = 0; w <= n; w++) if (f[n][1][w] >= lim) return cout << n - w << endl, 0;assert(false);return 0;
}