【题解】CF 1582G Kuzya and Homework

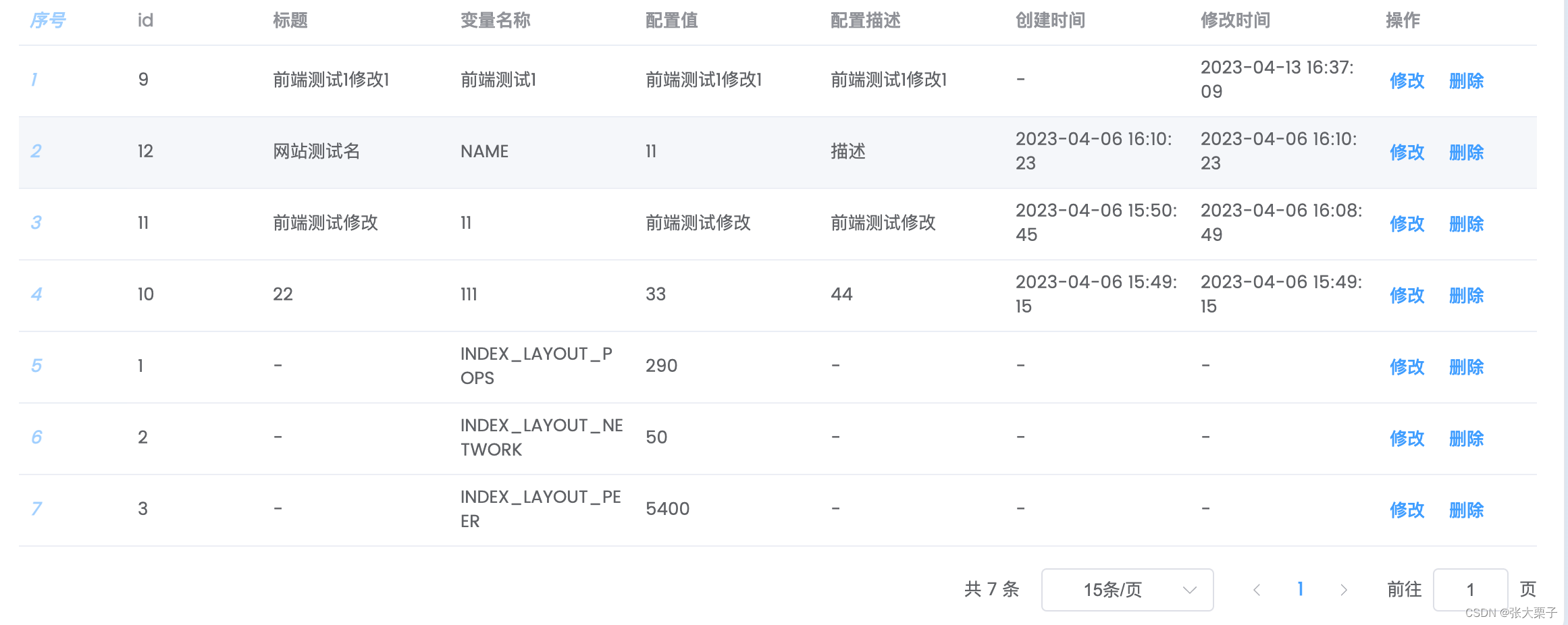
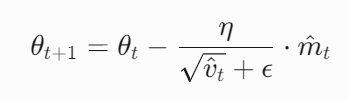要求结果为整数，我们将所有 \(a_i\) 分解质因数，对于每个质数分别考虑。

考虑对于一个左端点 \(l\)，能满足要求的右端点一定在从 \(l\) 开始的一段连续区间中。于是我们得对于每个 \(l\) 求出 \(ans_l\) 表示那个最远的右端点。

对于一个质数 \(p\)，假设 \(a_i\) 中有 \(k\) 个 \(p\)，如果 \(b_i\) 为乘号就在 \(i\) 这里记一个 \(k\)，否则记一个 \(-k\)。然后再做一个前缀和 \(pre\)。那么对于 \(l\)，我们要求的就是最大的 \(r\)，满足 \(\forall k\in[l,r],pre_k-pre_{l-1}\ge 0\)。可以倒着扫，维护一个单调栈，每次在单调栈上二分。但是这样的时间复杂度是无法承受的。我们考虑如果 \(a_i\) 中没有 \(p\)，那么 \(i\) 这个位置的答案就是等于 \(i+1\) 的答案的。于是我们只用存储那些包括了 \(p\) 的位置。于是就成了若干次区间的取 \(\min\)。再用并查集扫一遍即可。

先将所有质数都筛出来，时间复杂度可以承受。

#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
#define pii pair<int,int>
#define mp make_pair
#define fir first
#define sec second
#define lwrb lower_bound
using namespace std;
namespace asbt{
namespace cplx{bool begin;}
const int maxn=1e6+5,inf=0x3f3f3f3f;
int n,prn,a[maxn];
int prm[maxn],pre[maxn];
int zh1[maxn],zh2[maxn];
int fa[maxn],ans[maxn];
bool npr[maxn];
string b;
vector<pii> wei[maxn],cun[maxn];
il void init(int x){for(int i=2;i<=x;i++){if(!npr[i]){prm[++prn]=i;}for(int j=i*i;j<=x;j+=i){npr[j]=1;}}
}
il int find(int x){return x!=fa[x]?fa[x]=find(fa[x]):x;
}
namespace cplx{bool end;il double usdmem(){return (&begin-&end)/1048576.0;}
}
int main(){ios::sync_with_stdio(0),cin.tie(0);cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}cin>>b;b=" "+b;init(1e3);for(int i=1,tmp;i<=n;i++){tmp=a[i];for(int j=1,cnt;j<=prn&&prm[j]<=tmp/prm[j];j++){if(tmp%prm[j]==0){cnt=0;while(tmp%prm[j]==0){tmp/=prm[j],cnt++;}wei[prm[j]].pb(mp(i,b[i]=='*'?cnt:-cnt));}}if(tmp>1){wei[tmp].pb(mp(i,b[i]=='*'?1:-1));}}for(int i=1,top;i<=1e6;i++){if(wei[i].empty()){continue;}pre[0]=wei[i][0].sec;for(int j=1;j<wei[i].size();j++){pre[j]=pre[j-1]+wei[i][j].sec;}top=1;zh1[1]=-inf,zh2[1]=n+1;for(int j=wei[i].size()-1,k;~j;j--){while(top&&zh1[top]>pre[j]){top--;}zh1[++top]=pre[j],zh2[top]=wei[i][j].fir;k=lwrb(zh1+1,zh1+top+1,pre[j]-wei[i][j].sec)-zh1-1;cun[zh2[k]-1].pb(mp(j?wei[i][j-1].fir+1:1,wei[i][j].fir));}}for(int i=1;i<=n+1;i++){fa[i]=i,ans[i]=n;}for(int i=0;i<=n;i++){for(pii j:cun[i]){for(int k=find(j.fir);k<=j.sec;k=find(k+1)){ans[k]=i;fa[find(k)]=find(k+1);}}}
//	for(int i=1;i<=n;i++){
//		cout<<ans[i]<<" ";
//	}
//	puts("");ll Ans=0;for(int i=1;i<=n;i++){Ans+=ans[i]-i+1;}cout<<Ans;return 0;
}
}
int main(){return asbt::main();}