- 点击跳转专栏=>Unity3D特效百例
- 点击跳转专栏=>案例项目实战源码
- 点击跳转专栏=>游戏脚本-辅助自动化
- 点击跳转专栏=>Android控件全解手册
- 点击跳转专栏=>Scratch编程案例
- 点击跳转=>软考全系列
- 点击跳转=>蓝桥系列
👉关于作者
专注于Android/Unity和各种游戏开发技巧,以及各种资源分享(网站、工具、素材、源码、游戏等)
有什么需要欢迎底部卡片私我,获取更多支持,交流让学习不再孤单。

👉实践过程
需要所有整理的文档可底部卡片联系我,直接发压缩包。
😜九宫重排
问题描述
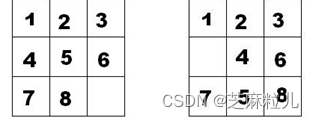
如图的第一个九宫格中,放着 1~8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动,可以形成第二个图所示的局面。
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
输入格式
输入第一行包含九宫的初态,第二行包含九宫的终态。
输出格式
输出最少的步数,如果不存在方案,则输出-1。
样例输入
12345678.
123.46758
样例输出
3
样例输入
13524678.
46758123.
样例输出
22
import java.io.*;
import java.util.*;
public class Main{static Map<String,Integer> hm1=new HashMap<String,Integer>();static Map<String,Integer> hm2=new HashMap<String,Integer>();public static void main(String args[]) throws IOException{BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));String start=bf.readLine();String end=bf.readLine();char[][] a=new char[3][3];char[][] b=new char[3][3];int c=0,x1=0,y1=0,x2=0,y2=0;for(int i=0;i<3;i++){for(int j=0;j<3;j++){a[i][j]=start.charAt(c);b[i][j]=end.charAt(c);c++;if(a[i][j]=='.'){x1=i;y1=j;}if(b[i][j]=='.'){x2=i;y2=j;}}}Node node1=new Node(0,x1,y1,a);Node node2=new Node(0,x2,y2,b);Queue<Node> qnode1=new LinkedList<Node>();Queue<Node> qnode2=new LinkedList<Node>();qnode1.add(node1);qnode2.add(node2);hm1.put(node1.gettu(), 0);hm2.put(node2.gettu(), 0);System.out.println(bfs(qnode1,qnode2));}public static int bfs(Queue<Node> q1,Queue<Node> q2){while(!q1.isEmpty()||!q2.isEmpty()){if(!q1.isEmpty()){Node node=q1.poll();int x=node.getX();int y=node.getY();if(hm2.containsKey(node.gettu())){return node.getSum()+hm2.get(node.gettu());}if(x>0){char[][] c=node.getCopy();c[x][y]=c[x-1][y];c[x-1][y]='.';Node node2=new Node(node.sum+1,x-1,y,c);String s=node2.gettu();if(hm2.containsKey(s)){return node2.getSum()+hm2.get(node2.gettu());}if(!hm1.containsKey(s)){hm1.put(s,node2.getSum());q1.add(node2);}}if(x<2){char[][] c=node.getCopy();c[x][y]=c[x+1][y];c[x+1][y]='.';Node node2=new Node(node.sum+1,x+1,y,c);String s=node2.gettu();if(hm2.containsKey(s)){return node2.getSum()+hm2.get(s);}if(!hm1.containsKey(s)){hm1.put(s,node2.getSum());q1.add(node2);}}if(y>0){char[][] c=node.getCopy();c[x][y]=c[x][y-1];c[x][y-1]='.';Node node2=new Node(node.sum+1,x,y-1,c);String s=node2.gettu();if(hm2.containsKey(s)){return node2.getSum()+hm2.get(s);}if(!hm1.containsKey(s)){hm1.put(s,node2.getSum());q1.add(node2);}}if(y<2){char[][] c=node.getCopy();c[x][y]=c[x][y+1];c[x][y+1]='.';Node node2=new Node(node.sum+1,x,y+1,c);String s=node2.gettu();if(hm2.containsKey(s)){return node2.getSum()+hm2.get(s);}if(!hm1.containsKey(s)){hm1.put(s,node2.getSum());q1.add(node2);}}}if(!q2.isEmpty()){Node node=q2.poll();int x=node.getX();int y=node.getY();if(hm1.containsKey(node.gettu())){return node.getSum()+hm1.get(node.gettu());}if(x>0){char[][] c=node.getCopy();c[x][y]=c[x-1][y];c[x-1][y]='.';Node node2=new Node(node.sum+1,x-1,y,c);String s=node2.gettu();if(hm1.containsKey(s)){return node2.getSum()+hm1.get(s);}if(!hm2.containsKey(s)){hm2.put(s,node2.getSum());q2.add(node2);}}if(x<2){char[][] c=node.getCopy();c[x][y]=c[x+1][y];c[x+1][y]='.';Node node2=new Node(node.sum+1,x+1,y,c);String s=node2.gettu();if(hm1.containsKey(s)){return node2.getSum()+hm1.get(s);}if(!hm2.containsKey(s)){hm2.put(s,node2.getSum());q2.add(node2);}}if(y>0){char[][] c=node.getCopy();c[x][y]=c[x][y-1];c[x][y-1]='.';Node node2=new Node(node.sum+1,x,y-1,c);String s=node2.gettu();if(hm1.containsKey(s)){return node2.getSum()+hm1.get(s);}if(!hm2.containsKey(s)){hm2.put(s,node2.getSum());q2.add(node2);}}if(y<2){char[][] c=node.getCopy();c[x][y]=c[x][y+1];c[x][y+1]='.';Node node2=new Node(node.sum+1,x,y+1,c);String s=node2.gettu();if(hm1.containsKey(s)){return node2.getSum()+hm1.get(s);}if(!hm2.containsKey(s)){hm2.put(s,node2.getSum());q2.add(node2);}}}}return -1;}
}
class Node{int sum,x,y;char[][] c=null;public char[][] getCopy(){char[][] copy=new char[3][3];for(int i=0;i<3;i++){for(int j=0;j<3;j++){copy[i][j]=c[i][j];}}return copy;}public String gettu(){StringBuffer s=new StringBuffer();for(int i=0;i<3;i++){for(int j=0;j<3;j++){s.append(c[i][j]);}}return s.toString();}public Node(int sum, int x, int y, char[][] c) {super();this.sum = sum;this.x = x;this.y = y;this.c = c;}public int getSum() {return sum;}public void setSum(int sum) {this.sum = sum;}public int getX() {return x;}public void setX(int x) {this.x = x;}public int getY() {return y;}public void setY(int y) {this.y = y;}
}😜格子刷油漆
问题描述
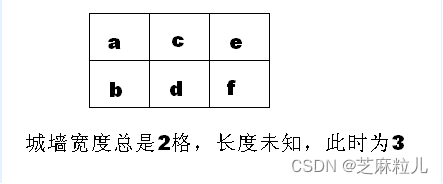
X国的一段古城墙的顶端可以看成 2*N个格子组成的矩形(如图所示),现需要把这些格子刷上保护漆。
你可以从任意一个格子刷起,刷完一格,可以移动到和它相邻的格子(对角相邻也算数),但不能移动到较远的格子(因为油漆未干不能踩!)
比如:a d b c e f 就是合格的刷漆顺序。
c e f d a b 是另一种合适的方案。
当已知 N 时,求总的方案数。当N较大时,结果会迅速增大,请把结果对 1000000007 (十亿零七) 取模。
输入格式
输入数据为一个正整数(不大于1000)
输出格式
输出数据为一个正整数。
样例输入
2
样例输出
24
样例输入
3
样例输出
96
样例输入
22
样例输出
359635897
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {public static void main(String[] args) throws NumberFormatException, IOException {BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));int n=Integer.parseInt(bfr.readLine());long sum=0,mod=1000000007;long[] A=new long[n+1];long[] B=new long[n+1];A[1]=1; A[2]=2;B[1]=1; B[2]=6;int i,j;for(i=3;i<=n;i++){A[i]=2*A[i-1]%mod;B[i]=(2*B[i-1]%mod+2*A[i-2]%mod+B[i-2]*2%mod+2*A[i-2]%mod+2*B[i-2]%mod)%mod;}sum=4*B[n]%mod;for(j=2;j<n;j++){sum+=(2*(A[j-1]*2*B[n-j]*2%mod+2*A[n-j]*2*B[j-1]%mod));sum%=mod;}if(n>1) System.out.println(sum);else System.out.println(2);}😜回文数字
问题描述
观察数字:12321,123321 都有一个共同的特征,无论从左到右读还是从右向左读,都是相同的。这样的数字叫做:回文数字。
本题要求你找到一些5位或6位的十进制数字。满足如下要求:
该数字的各个数位之和等于输入的整数。
输入格式
一个正整数 n (10<n<100), 表示要求满足的数位和。
输出格式
若干行,每行包含一个满足要求的5位或6位整数。
数字按从小到大的顺序排列。
如果没有满足条件的,输出:-1
样例输入
44
样例输出
99899
499994
589985
598895
679976
688886
697796
769967
778877
787787
796697
859958
868868
877778
886688
895598
949949
958859
967769
976679
985589
994499
样例输入
60
样例输出
-1
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;public class Main
{public static void main(String args[]) throws IOException{BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));String str1 = bf.readLine();int n = Integer.parseInt(str1);int t = 0;for (int i = 1; i <= 9; i++)for (int j = 0; j <= 9; j++)for (int k = 0; k <= 9; k++){if (n == 2 * (i + j) + k){System.out.println(i * 10000 + j * 1000 + k * 100 + j* 10 + i);t = 1;}}for (int i = 1; i <= 9; i++)for (int j = 0; j <= 9; j++)for (int k = 0; k <= 9; k++){if (n == 2 * (i + j + k)){System.out.println(i * 100000 + j * 10000 + k * 1000+ k * 100 + j * 10 + i);t = 1;}}if (t == 0)System.out.println("-1");}
}😜国王的烦恼
问题描述
C国由n个小岛组成,为了方便小岛之间联络,C国在小岛间建立了m座大桥,每座大桥连接两座小岛。两个小岛间可能存在多座桥连接。然而,由于海水冲刷,有一些大桥面临着不能使用的危险。
如果两个小岛间的所有大桥都不能使用,则这两座小岛就不能直接到达了。然而,只要这两座小岛的居民能通过其他的桥或者其他的小岛互相到达,他们就会安然无事。但是,如果前一天两个小岛之间还有方法可以到达,后一天却不能到达了,居民们就会一起抗议。
现在C国的国王已经知道了每座桥能使用的天数,超过这个天数就不能使用了。现在他想知道居民们会有多少天进行抗议。
输入格式
输入的第一行包含两个整数n, m,分别表示小岛的个数和桥的数量。
接下来m行,每行三个整数a, b, t,分别表示该座桥连接a号和b号两个小岛,能使用t天。小岛的编号从1开始递增。
输出格式
输出一个整数,表示居民们会抗议的天数。
样例输入
4 4
1 2 2
1 3 2
2 3 1
3 4 3
样例输出
2
样例说明
第一天后2和3之间的桥不能使用,不影响。
第二天后1和2之间,以及1和3之间的桥不能使用,居民们会抗议。
第三天后3和4之间的桥不能使用,居民们会抗议。
数据规模和约定
对于30%的数据,1<=n<=20,1<=m<=100;
对于50%的数据,1<=n<=500,1<=m<=10000;
对于100%的数据,1<=n<=10000,1<=m<=100000,1<=a, b<=n, 1<=t<=100000。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;public class Main {static int n;static int sum = 0;static int a[];static Edge p[];public static void main(String[] args) throws Exception {BufferedReader buf = new BufferedReader(new InputStreamReader(System.in));String read[] = buf.readLine().split("\\s+");n = Integer.parseInt(read[0]);int m = Integer.parseInt(read[1]);p = new Edge[m];a = new int[n];int s, e, w, t;for (int i = 0; i < m; i++) {read = buf.readLine().split("\\s+");s = Integer.parseInt(read[0]) - 1;e = Integer.parseInt(read[1]) - 1;w = Integer.parseInt(read[2]);p[i] = new Edge(s, e, w);}java.util.Arrays.sort(p);boolean flag = false;init();for (int i = 0; i < m; i++) {flag = false;s = p[i].s;e = p[i].e;if (!isConnect(s, e)) {flag = true;union(s, e);}while (i < m - 1 && p[i].w == p[i + 1].w) {s = p[i + 1].s;e = p[i + 1].e;if (flag && !isConnect(s, e))union(s, e);if (!flag && !isConnect(s, e)) {flag = true;union(s, e);}i++;}if (flag)sum++;}System.out.println(sum);}private static boolean isConnect(int i, int j) {if (find(i) == find(j))return true;return false;}private static void init() {for (int i = 0; i < n; i++)a[i] = i;}private static void union(int x, int y) {a[find(x)] = find(y);}private static int find(int x) {if (a[x] == x)return x;a[x] = find(a[x]);return a[x];}
}
class Edge implements Comparable<Edge> {int s;int e;int w;public Edge(int s, int e, int w) {super();this.s = s;this.e = e;this.w = w;}@Overridepublic int compareTo(Edge p) {if (this.w < p.w)return 1;else if (this.w > p.w)return -1;return 0;}}👉其他
📢作者:小空和小芝中的小空
📢转载说明-务必注明来源:https://zhima.blog.csdn.net/
📢这位道友请留步☁️,我观你气度不凡,谈吐间隐隐有王者霸气💚,日后定有一番大作为📝!!!旁边有点赞👍收藏🌟今日传你,点了吧,未来你成功☀️,我分文不取,若不成功⚡️,也好回来找我。
温馨提示:点击下方卡片获取更多意想不到的资源。