双向广搜
文章目录
前言
前言
复习acwing算法提高课的内容,本篇为讲解算法:双向广搜
一、双向广搜
双向广搜其实就是两个bfs,我们知道bfs是一种暴力的做题方法,搜索树长下图所示:
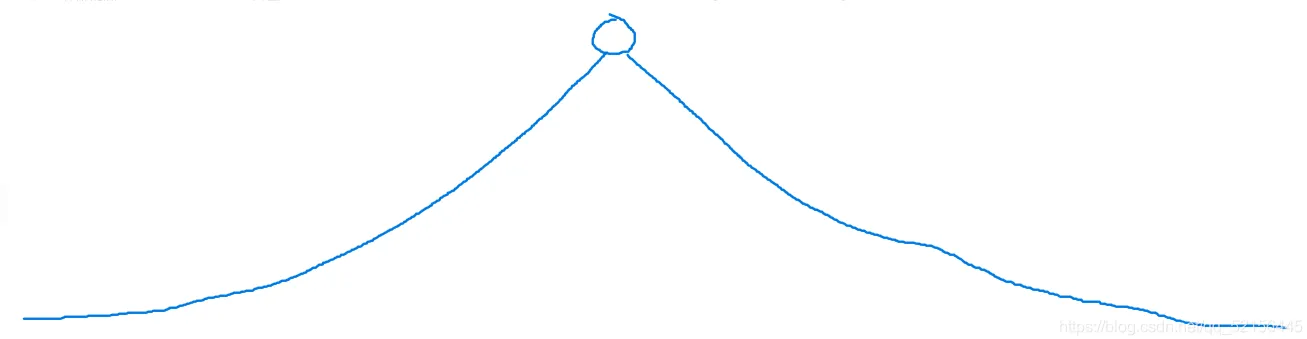
我们会发现搜索树越来越宽,每一层的搜索量增加,如果数据范围很大的话,显然是会TLE的,那么为了避免TLE,我们可以采用双向广搜,即两个bfs,如下图所示:
这个样子就可以省去很多不必要的搜索量,我们在这个基础上可以再次优化,每次只bfs一次,每次bfs那个队列容量少的部分。
二、AcWing 190. 字串变换
本题链接:AcWing 190. 字串变换
本博客提供本题截图:

本题分析
定义两个队列,分别表示开始和末尾,进行双向广搜,我们每次挑出来含元素少的队列进行bfs,qa表示从起始位置开始的bfs,qb表示的是从结尾开始的bfs,da表示的距离是从起始到当前的距离,db表示的距离是从结尾到当前的距离,extend表示的是扩展的过程,这里需要注意的话如果是对qb执行extend操作的话,是把b变成a
对于extend操作:
if (da.count(state)) continue;
if (db.count(state)) return da[t] + 1 + db[state];如果state出现在da,那么证明被更新过,直接continue这种情况
如果state出现在db,那么证明已经找到了最后的结果,即双向光搜碰头了,那么就把距离返回给main
AC代码
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <queue>using namespace std;const int N = 6;int n;
string a[N], b[N];int extend(queue<string>& q, unordered_map<string, int>& da, unordered_map<string, int>& db, string a[], string b[])
{for (int k = 0, sk = q.size(); k < sk; k ++ ){string t = q.front();q.pop();for (int i = 0; i < t.size(); i ++ )for (int j = 0; j < n; j ++ )if (t.substr(i, a[j].size()) == a[j]){string state = t.substr(0, i) + b[j] + t.substr(i + a[j].size());if (da.count(state)) continue;if (db.count(state)) return da[t] + 1 + db[state];da[state] = da[t] + 1;q.push(state);}}return 11;
}int bfs(string A, string B)
{queue<string> qa, qb;unordered_map<string, int> da, db;qa.push(A), da[A] = 0;qb.push(B), db[B] = 0;while (qa.size() && qb.size()){int t;if (qa.size() <= qb.size()) t = extend(qa, da, db, a, b);else t= extend(qb, db, da, b, a);if (t <= 10) return t;}return 11;
}int main()
{string A, B;cin >> A >> B;while (cin >> a[n] >> b[n]) n ++ ;int step = bfs(A, B);if (step > 10) puts("NO ANSWER!");else printf("%d\n", step);return 0;
}