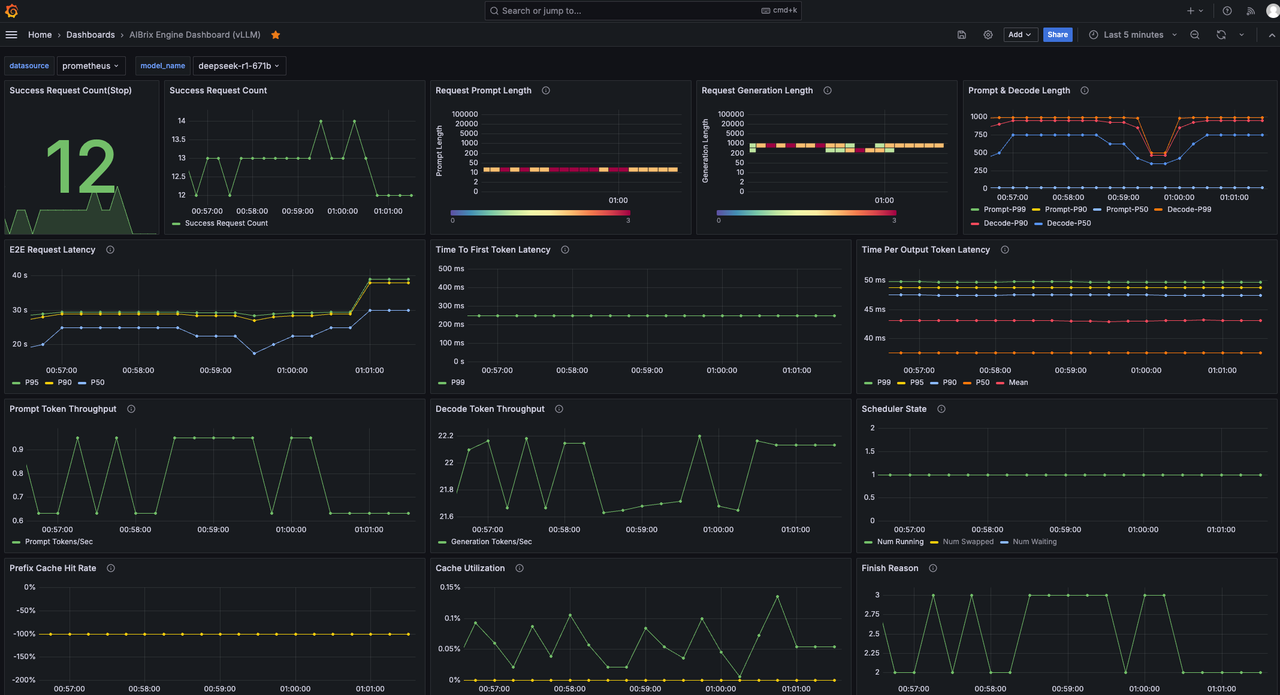
题目:
from Crypto.Util.number import *
from flag import flagdef on_barak(P, E):c, d, p = Ex, y = Preturn (x**3 + y**3 + c - d*x*y) % p == 0def add_barak(P, Q, E):if P == (0, 0):return Qif Q == (0, 0):return Passert on_barak(P, E) and on_barak(Q, E)x1, y1 = Px2, y2 = Qif P == Q:x3 = y1 * (c - x1**3) * inverse(x1**3 - y1**3, p) % py3 = x1 * (y1**3 - c) * inverse(x1**3 - y1**3, p) % pelse:x3 = (y1**2*x2 - y2**2*x1) * inverse(x2*y2 - x1*y1, p) % py3 = (x1**2*y2 - x2**2*y1) * inverse(x2*y2 - x1*y1, p) % preturn (x3, y3)def mul_barak(m, P, E):if P == (0, 0):return PR = (0, 0)while m != 0:if m & 1:R = add_barak(R, P, E)m = m >> 1if m != 0:P = add_barak(P, P, E)return Rdef rand_barak(E):c, d, p = Ewhile True:y = randint(1, p - 1)K = Zmod(p)P.<x> = PolynomialRing(K) f = x**3 - d*x*y + c + y^3R = f.roots()try:r = R[0][0]return (r, y)except:continuep = 73997272456239171124655017039956026551127725934222347
d = 68212800478915688445169020404812347140341674954375635
c = 1
E = (c, d, p)P = rand_barak(E)FLAG = flag.lstrip(b'CCTF{').rstrip(b'}')
m = bytes_to_long(FLAG)
assert m < p
Q = mul_barak(m, P, E)
print(f'P = {P}')
print(f'Q = {Q}')
'''
P = (71451574057642615329217496196104648829170714086074852,69505051165402823276701818777271117086632959198597714)
Q = (40867727924496334272422180051448163594354522440089644,56052452825146620306694006054673427761687498088402245)
'''
解题思路:
分析曲线
-
其一般方程的形式为
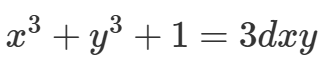 -
分析曲线结构
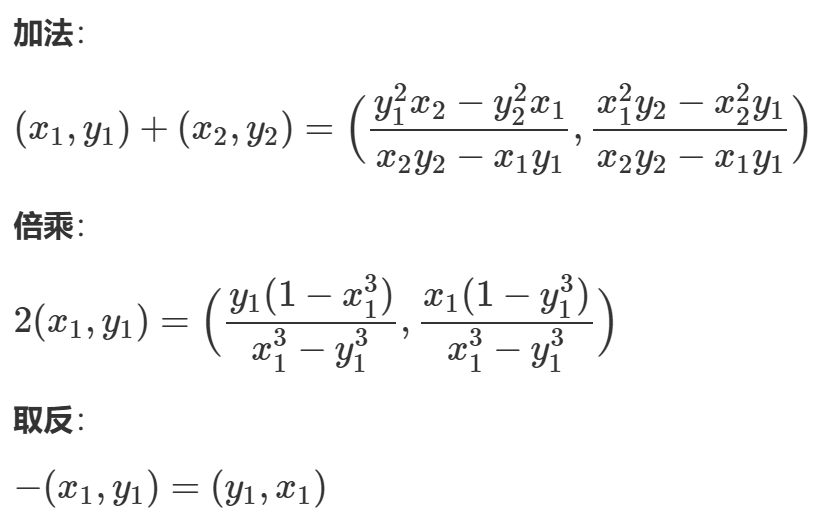
分析代码
**P**:随机生成的椭圆曲线上的一个点**Q**:通过标量乘法mul_barak(m, P, E)得到的加密点**E**:椭圆曲线的参数,是一个元组(c, d, p)**c**:椭圆曲线方程中的常数项**d**:椭圆曲线方程中的系数**p**:一个质数,表示椭圆曲线的模数,用于定义有限域Fp
函数的作用省略了,和前面的都一样
解答思路
- 换元映射
- 需要引入一个变量
z来把它变成齐次式x^3+y^3+c*z^3=dxyz - (类似于下面的Twisted Hessian曲线的做法)
- 当
z=1时即为原方程,然后就通过映射,将原曲线中的点映射到椭圆曲线上,看了一下构造出来的椭圆曲线的阶是光滑的,所以直接求个离散对数就行了 - 又因为随机点
PP不是椭圆曲线的生成元,所以我们还需要加上PP阶的倍数去枚举结果
解答:
p = 73997272456239171124655017039956026551127725934222347
c = 1
d = 68212800478915688445169020404812347140341674954375635Zp = Zmod(p)
R.<x,y,z> = Zp[]
cubic = x^3 + y^3 + c * z^3 - d * x * y * z
EC = EllipticCurve_from_cubic(cubic, morphism=False)
mf = EllipticCurve_from_cubic(cubic, morphism=True)print(EC.order())
#73997272456239171124655016995459084401465136460086688
P = (71451574057642615329217496196104648829170714086074852, 69505051165402823276701818777271117086632959198597714)
Q = (40867727924496334272422180051448163594354522440089644, 56052452825146620306694006054673427761687498088402245)PP = mf(P)
QQ = mf(Q)
dd = PP.discrete_log(QQ)
print(PP.order())
#3083219685676632130193959041477461850061047352503612
print(dd)
#1780694557271320552511299360138314441283923223949197
for i in range(100):m = dd + i * PP.order()hex_m = hex(m)[2:].lstrip('0')if len(hex_m) % 2 != 0:hex_m = '0' + hex_mtry:flag = bytes.fromhex(hex_m)print(flag)except ValueError as e:print(f"Error in candidate {i}: {e}")
#CCTF{_hE5S!4n_f0rM_0F_3CC!!}
下面这个脚本我本打算用Pohlig_Hellman函数
def Pohlig_Hellman(n,P,Q):factors, exponents = zip(*factor(n))primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-1]print(primes)dlogs = []for fac in primes:t = int(int(P.order()) // int(fac))dlog = discrete_log(t*Q,t*P,operation="+")dlogs += [dlog]print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime ordernum2 = crt(dlogs,primes)return num2
不过手动计算跟sagemath内置的求离散对数的结果不同,所以改为使用内置函数
mf = EllipticCurve_from_cubic(cubic, morphism=True)
PP = mf(P)
QQ = mf(Q)
dd = PP.discrete_log(QQ)
p = 73997272456239171124655017039956026551127725934222347
a = 1
P = (71451574057642615329217496196104648829170714086074852, 69505051165402823276701818777271117086632959198597714)
Q = (40867727924496334272422180051448163594354522440089644, 56052452825146620306694006054673427761687498088402245)
d = ZZ((a*P[0]**3 + P[1]**3 + 1) * inverse_mod(P[0]*P[1], p) % p)
print(d)
#68212800478915688445169020404812347140341674954375635# construct ECC to get a solution of X^3+Y^3+Z^3=dXYZ
R.<x,y,z> = Zmod(p)[]
cubic = x^3 + y^3 + z^3 - d*x*y*z
E = EllipticCurve_from_cubic(cubic,morphism=True)
mf = EllipticCurve_from_cubic(cubic, morphism=True)PP = mf(P)
QQ = mf(Q)
dd = PP.discrete_log(QQ)
print(dd)
#1780694557271320552511299360138314441283923223949197
P = E(P)
Q = E(Q)
P_ord = P.order()
print(P_ord)
#3083219685676632130193959041477461850061047352503612
for i in range(100):m = dd + i * P_ordhex_m = hex(m)[2:].lstrip('0')if len(hex_m) % 2 != 0:hex_m = '0' + hex_mtry:flag = bytes.fromhex(hex_m)print(flag)except ValueError as e:print(f"Error in candidate {i}: {e}")
#CCTF{_hE5S!4n_f0rM_0F_3CC!!}