GPU内核实现（上）

GPU内核实现

以下是基于CSR和ELLPACK格式的一些标准SpMV实现。

1. 标量CSR内核

GPU加速SpMV的最简单实现之一是标量内核方法。标量内核分配一个线程来处理SpMV中的每个稀疏点积。稀疏点积由每个线程以顺序方式处理，从而消除了对需要共享内存和/或扭曲级别降低的更高级技术的需求。以下代码片段显示了标量CSR内核的直接实现。

__global__ void scalar_csr_kernel(const int m,

                                  const int *__restrict__ row_offsets,

                                  const int *__restrict__ cols,

                                  const double *__restrict__ vals,

                                  const double *__restrict__ x,

                                  double *__restrict__ y,

                                  const double alpha,

                                  const double beta)

{

  const int row = threadIdx.x + blockDim.x * blockIdx.x;

  if (row < m) {

    // 确定每一行的开始和结束

    int p = row_offsets[row];

    int q = row_offsets[row+1];

 

    // 运行全稀疏行*向量点积运算

    double sum = 0;

    for (int i = p; i < q; i++) {

      sum += vals[i] * x[cols[i]];

    }

    // 写到内存

    if (beta == 0) {

      y[row] = alpha * sum;

    } else {

      y[row] = alpha * sum + beta * y[row];

    }

  }

}

void scalar_csr(int m,

                int threads_per_block,

                int * row_offsets,

                int * cols,

                double * vals,

                double * x,

                double * y,

                double alpha,

                double beta)

{

  int num_blocks = (m + threads_per_block - 1) / threads_per_block;

  dim3 grid(num_blocks, 1, 1);

  dim3 block(threads_per_block, 1, 1);

  scalar_csr_kernel<<<grid, block>>>(m, row_offsets, cols, vals, x, y, alpha, beta);

}

如上所述，计算仅在行之间并行化。设

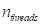
 每个块中的线程数为1，则完成计算所需的独立块数通过天花板函数计算为：

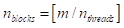
 （10-1）

在这种情况下，

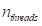
 是一个可调参数，可以使用它来最大限度地提高此实现的性能。

1）根据线程和块的简单映射计算 ROW。

2）确保不会读取超出行偏移量数组中的任何数组边界。

3）确定要通过相邻读取行偏移量数组来加载的列（以及向量）索引和矩阵值。

4）对稀疏点积进行标量计算。

5）将结果写入内存。

在最后一步中，可以通过测试向量是否被覆盖或更新来节省一些内存带宽。

标量CSR实现，将在最广泛的稀疏矩阵范围内实现平庸的性能。然而，在某些情况下，这种内核可能会适度有效，即每行非零的平均数量很小。事实上，当每行非零的平均数量很高时，将需要多个请求来为内存事务提供服务，并且合并将是最小的。相比之下，当每行非零的平均数量非常低时，高内存带宽可以与此内核的简单性相结合，以实现良好的性能。

2. 向量CSR内核

GPU加速的SpMV最通用的高性能实现是向量核方法。与标量核不同，向量核在扭曲中使用warp多个线程来减少每个稀疏点积。它需要共享内存或扭曲洗牌操作来减少跨线程计算的部分减少的值。用于选择分配给每个稀疏行向量乘积的每个扭曲的线程数的启发式方法是基于

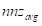
 。通常，通过找到小于或等于2的最小幂来找到最佳性能

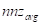
 。此时，研究一个代码示例以检查实现的细节是有帮助的。这里关注的是只使用扭曲洗牌操作来完成稀疏点积的情况。应当注意，每个输出结果可以通过不超过波阵面大小的线程计算，在MI200架构上为64。当每行非零的平均数量远大于波前尺寸时，这可能会限制性能。

template <int THREADS_PER_ROW>

__global__ void vector_csr_kernel(const int m,

                                  const int *__restrict__ row_offsets,

                                  const int *__restrict__ cols,

                                  const double *__restrict__ vals,

                                  const double *__restrict__ x,

                                  double *__restrict__ y,

                                  const double alpha,

                                  const double beta)

{

  const int row = threadIdx.y + blockDim.y * blockIdx.x;

  if (row < m) {

    // 确定每一行的开始和结束

    int p = row_offsets[row];

    int q = row_offsets[row+1];

    // 开始稀疏行*向量点积运算

    double sum = 0;

    for (int i = p + threadIdx.x; i < q; i += THREADS_PER_ROW) {

      sum += vals[i] * x[cols[i]];

    }

    // 结束稀疏行*向量点积运算

#pragma unroll

    for (int i = THREADS_PER_ROW >> 1; i > 0; i >>= 1)

      sum += __shfl_down(sum, i, THREADS_PER_ROW);

    // 写到内存

    if (!threadIdx.x) {

      if (beta == 0) {

        y[row] = alpha * sum;

      } else {

        y[row] = alpha * sum + beta * y[row];

      }

    }

  }

}

void vector_csr(int m,

                int threads_per_block,

                int warpSize,

                int * row_offsets,

                int * cols,

                double * vals,

                double * x,

                double * y,

                double alpha,

                double beta)

{

  int nnz_per_row = nnz / m;

  int threads_per_row = prevPowerOf2(nnz_per_row);

  // 将每行的线程数限制为不大于波前（扭曲）大小

  threads_per_row = threads_per_row > warpSize ? warpSize: 

threads_per_row;

  int rows_per_block = threads_per_block / threads_per_row;

  int num_blocks = (m + rows_per_block - 1) / rows_per_block;

  dim3 grid(num_blocks, 1, 1);

  dim3 block(threads_per_row, rows_per_block, 1);

  if (threads_per_row <= 2)

      vector_csr_kernel<2><<<grid, block>>>(m, row_offsets, cols, vals, x, y, alpha, beta);

  else if (threads_per_row <= 4)

      vector_csr_kernel<4><<<grid, block>>>(m, row_offsets, cols, vals, x, y, alpha, beta);

 ...

  else if (threads_per_row <= 32)

      vector_csr_kernel<32><<<grid, block>>>(m, row_offsets, cols, vals, x, y, alpha, beta);

  else

      vector_csr_kernel<64><<<grid, block>>>(m, row_offsets, cols, vals, x, y, alpha, beta);

}

此实现与标量实现有几个关键区别。用

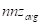
 来构建一个二维线程块。

1）线程的X维度表示分配给每行的线程数。这是通过函数prevPowerOf2计算的，该函数计算小于或等于输入变量2的最小幂。

2）Y维度表示每个线程块的行数。

3）线程块的总数由每个块处理的行数决定。

模板用于启动内核，每行的线程数变为编译时常量。这样可以在循环展开期间优化归约算法。

内核的开头方式与标量内核类似，但有一个关键区别在于如何从 Block/Grid Launch 启发式方法计算行索引。使用线程索引的y分量和块大小来计算这个值。然后，稀疏点积被分解为两个步骤。

1）每个线程以模板参数的倍数在行上循环，计算稀疏点积的部分结果。

2）完成后，subwarp 将使用 向下shuffle操作，将值累加到每个波前中的线程0。

注意到稀疏点积步骤的任何一部分都缺乏同步步骤。这是由于将自己限制在至少与波阵面大小一样小的减小量上。