3. ELLPACK 内核
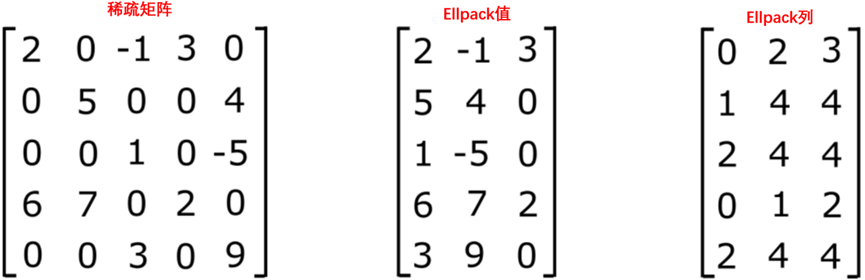
ELLPACK SpMV实现沿行并行计算。由于数据已被重新排序为以列为主存储,因此沿ELLPACK数据连续行的内存访问被合并。在下面显示的实现中,假设输入cols和vals数组已经转换为ELLPACK格式。这种格式的一个关键部分是元数据参数,即每行非零的最大数量,它也作为参数传递。
__global__ void ellpack_kernel(const int m,
const int max_nnz_per_row,
const int *__restrict__ cols,
const double *__restrict__ vals,
const double *__restrict__ x,
double *__restrict__ y,
const double alpha,
const double beta)
{
const int row = threadIdx.x + blockDim.x * blockIdx.x;
if (row < m) {
double sum = 0;
for (int i=row; i < max_nnz_per_row*m; i+=m)
{
sum += vals[i] * x[cols[i]];
}
// 写到内存
if (beta == 0) {
y[row] = alpha * sum;
} else {
y[row] = alpha * sum + beta * y[row];
}
}
}
void ellpack(int m,
int threads_per_block,
int max_nnz_per_row,
int * cols,
double * vals,
double * x,
double * y,
double alpha,
double beta)
{
int num_blocks = (m + threads_per_block - 1) / threads_per_block;
dim3 grid(num_blocks, 1, 1);
dim3 block(threads_per_block, 1, 1);
ellpack_kernel<<<grid, block>>>(m, max_nnz_per_row, cols, vals, x, y, alpha, beta);
}
跨线程块的工作分解与标量csr格式相同。此外,稀疏点积也以标量方式执行。此内核和标量CSR内核之间的关键区别在于,矩阵是以合并的方式访问的。数据结构中的填充,能够在稀疏点积实现中,编写没有昂贵条件的代码。
参阅以下示例,了解如何从矩阵市场文件输入运行ELLPACK内核。此示例包括将设备从CSR格式转换为ELLPACK。
4. 阻止 ELLPACK 内核
被阻塞的ELLPACK数据结构,旨在最大限度地减少ELLPACK结构中,引入额外内存读取。每行的最大条目数是在一组行内计算的,该组行是波前大小的倍数。然后,在每个块中计算局部ELLPACK结构。然后将每个块连接起来形成全局数据结构。这需要一个额外的小数组,类似于CSR行偏移量,以每行最大列数表示每个块的开始和结束。
下面的代码片段显示了一个实现。首先要注意的是,该代码是在波阵面大小的对数基2上模板化的,以避免用于计算全局波指数的整数除法。全局波浪指数用于从内核中立即返回那些在计算中不起作用的尾随波浪。
template<int LOG2WFSIZE>
__global__ void blocked_ellpack_kernel(const int m,
const int tw,
const int *__restrict__ max_nnz_per_row_per_warp,
const int *__restrict__ cols,
const double *__restrict__ vals,
const double *__restrict__ x,
double *__restrict__ y,
const double alpha,
const double beta)
{
const int row = threadIdx.x + blockDim.x * blockIdx.x;
const int warp = row>>LOG2WFSIZE;
if (warp>=tw) return;
const int lane = row&(warpSize-1);
int p = max_nnz_per_row_per_warp[warp];
int q = max_nnz_per_row_per_warp[warp+1];
p<<=LOG2WFSIZE;
q<<=LOG2WFSIZE;
if (row < m) {
// 稀疏点积实现
double sum = 0;
for (p+=lane; p<q; p+=warpSize)
{
sum += vals[p] * x[cols[p]];
}
// 写到内存
if (beta == 0) {
y[row] = alpha * sum;
} else {
y[row] = alpha * sum + beta * y[row];
}
}
}
了解如何从矩阵市场文件输入运行Block ELLPACK内核。此示例包括将设备从CSR格式转换为Block ELLPACK。
5. 性能分析
为了衡量各种实现的性能,从各种来源中选择矩阵。首先,从Suiteparse矩阵集合中收集了一些经典示例。这些矩阵在图10-4中有黑色标签。
从ExaWind项目中收集了几种类型的矩阵。ExaWind项目旨在模拟整个风电场在大气边界层中的复杂流体运动。求解器由背景(AMR Wind)和叶片解析求解器(Nalu Wind)组成,分别尝试捕捉大尺度和小尺度行为。背景解算器有几个泊松样解算器,可以从7点和27点模板中生成结构化矩阵。这些矩阵在图10-4中有红色标签。叶片解析求解器使用非结构化网格来模拟风力涡轮机叶片和塔架周围的流体运动。使用来自背景求解器压力泊松解的不同大小网格的矩阵。Nalu Wind利用Hypre Boomer AMG(Algrebraic Multigrid)算法求解压力泊松方程。AMG求解器层次结构产生了具有有趣结构的稀疏矩阵。Nalu Wind和Hypre的非结构化矩阵在图10-4中具有蓝色标签。
Pele ECP项目旨在以超高分辨率模拟复杂几何结构内的燃烧过程。Pele利用自适应网格细化技术与嵌入式边界算法相结合,实现了前所未有的计算规模。与AMR Wind类似,该应用程序需要求解泊松矩阵,以推进底层物理方程求解器。从这些泊松问题中提取了几个矩阵,包括小问题和大问题。这些矩阵具有值得进一步研究的有趣结构,在图10-4中用绿色标记。
显示了单个MI250X GCD的性能结果,如图10-4所示。除了上面提供的代码示例外,还提供了一个如何从矩阵市场文件输入运行rocSPARSE CSR内核的示例。
对于每个内核,每个块使用256个线程。每个块还生成了128和512个线程的结果,这些线程通常比256个线程略差。在图10-4左图中,显示了按默认RocSparse性能缩放的每次SpMV执行的平均时间。在图10-4右图中,显示了按三种格式的平均SpMV定时缩放的设置成本,其中需要从CSR格式转换(ELLPACK和块ELLPACK),或者需要对CSR矩阵进行分析(RocSparseWithAnalysis)。
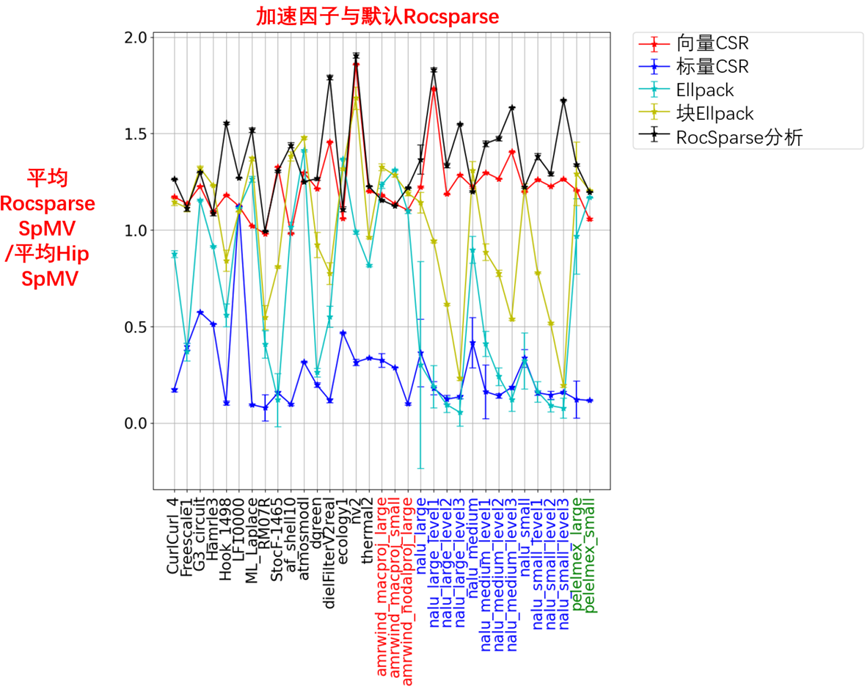
图10-4 单个MI250X GCD的性能结果
SpMV:设置与执行比率,如图10-5所示。
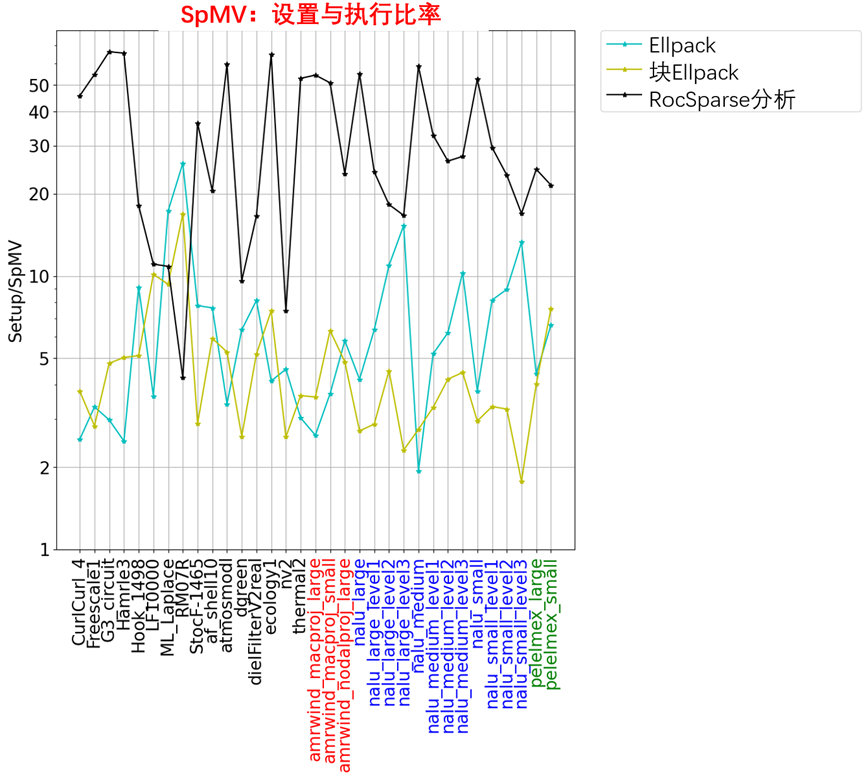
图10-5 SpMV:设置与执行比率
数据显示,这里考虑的矩阵集存在显著差异。使用RocSPARSE进行分析通常是最快的,但它的设置成本最高。该算法对于nnz每行分布中具有长尾的矩阵特别有效。Block ELLPACK实现通常非常好,特别是在每行nnz的方差很小的情况下。与Block ELLPACK相关的设置成本通常远低于Roc稀疏分析的成本,而且收益通常相当不错。
矩阵_nalu_large_level1_、_nalu_lage_level2_和_nalu_large_level3_具有长尾的nnz每行分布。nalu矩阵的中小型版本也是如此。图10-5中显示了_nalu_large_level2_的分布和稀疏模式。由于稀疏模式的分散性和nnz每行分布中的长尾,这些矩阵通常会导致ELLPACK存储格式中的大量0-fill。最终,ELLPACK内核的简单性,将无法克服从0填充值读取内存的大幅增加。这就解释了为什么这些实现的性能会显著下降。相比之下,具有分析功能的RocSparse内核被设计,用来很好地处理这些类型的矩阵。简单的Vector CSR内核,也能很好地处理这些情况。
6. 小结
这是使用HIP开发和优化一些基本SpMV内核的第一部分。对各种矩阵的性能,已经展示了几种不同存储格式。还展示了从CSR格式转换为ELLPACK和内部Rocsparse格式的性能成本。一般来说,Rocsparse分析算法提供了全面的最佳性能,但它的设置成本比这里考虑的其他格式更高。
由于SpMV算法通常嵌入在较大的算法中,如AMG,因此,在为特定问题选择最佳格式时,考虑完整的应用程序配置文件非常重要。

![洛谷 P1216 [IOI 1994] 数字三角形 Number Triangles (记忆化搜索)](https://img2024.cnblogs.com/blog/3612019/202503/3612019-20250329022938528-2081809026.png)