目录
- 一般最小二乘法
- 加权最小二乘
- 递推最小二乘
一般最小二乘法
无需每次对整体数据进行最小二乘估计,利用上次计算的值与当前数据融合计算,获取计算结果。本质上是对老的计算结果修正的方式,节省计算步骤,降低运算量,提升计算的效率。
若辨识模型:
\[z_{(k)}={h_{(k)}}^T\theta+v_{(k)}
\]
其中\(z_{(k)}\)为系统输出,\(h_{(k)}\)为系统输入,\(v_{(k)}\)为系统噪声,\(\theta\)为系统要辨识的参数集合构成的向量。
系统估计的损失函数:
\[J(\hat{\theta})={(z_m-{h_m}^T\hat{\theta})}^T{(z_m-{h_m}^T\hat{\theta})}
\]
确保损失函数最小,根据极值定理:
\[\frac{\partial J}{\partial \theta}|_{\theta=\hat \theta}=-2h_m(z_m-{h_m}^T\hat\theta)=0
\]
即:
\[\hat \theta={(h_m{h_m}^T)}^{-1}h_mz_m
\]
最小二乘估计的参数就出来了。
加权最小二乘
与一般最小二乘法不同的是,损失函数中包含加权矩阵:
\[W_m=diag[w_{(1)}, w_{(2)}, \ldots ,w_{(m)}]
\]
则损失函数为:
\[J(\hat{\theta})={(z_m-{h_m}^T\hat{\theta})}^TW_m{(z_m-{h_m}^T\hat{\theta})}
\]
则加权最小二乘估计:
\[\hat \theta={(h_mW_m{h_m}^T)}^{-1}h_mW_mz_m
\]
当\(W_m=R^{-1}\),\(R\)为噪声协方差矩阵,则为马尔科夫估计,是所有加权最小二乘估计的最优。
递推最小二乘
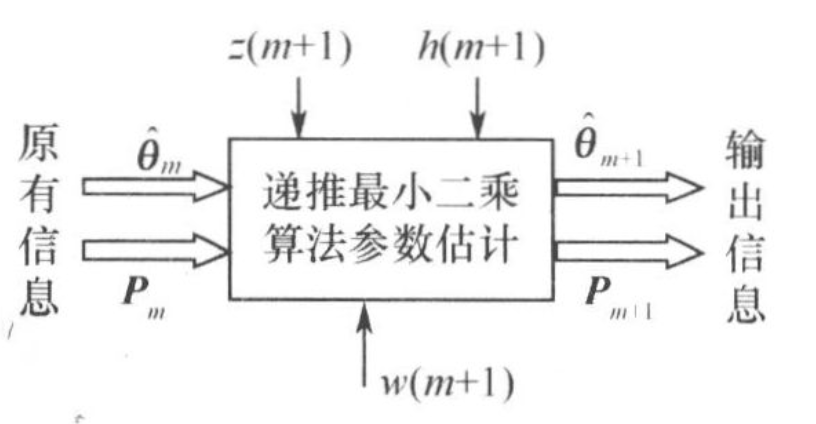
在加权最小二乘时,充分利用上时刻计算值与当前数据通过数据融合,增加计算的效率,减小计算的数据量,实现对以前数据的修正改善计算效果。
若\(m\)次数据的加权最小二乘估计:
\[\hat \theta_m={(h_mW_m{h_m}^T)}^{-1}h_mW_mz_m
\]
当\(m+1\)次的输入输出数据:
\[z_{(m+1)}={h_{(m+1)}}^T\theta+v_{(m+1)}
\]
数据和噪声方差融合系数:
\[K_{(m+1)}=\frac{P_m{h_{(m+1)}}^T}{{w_{(m+1)}}^{-1}+h_{(m+1)}P_m{h_{(m+1)}}^T}
\]
其中:
\(P_m=({h_m}^TW_mh_m)^{-1}\)为输入输出数据方差,\(w_{(m+1)}\)为噪声方差
当前输入输出数据方差:
\[\begin{align}
P_{(m+1)}&=P_m-\frac{P_m{h_{(m+1)}}^T{h_{(m+1)}}P_m}{{w_{(m+1)}}^{-1}+h_{(m+1)}P_m{h_{(m+1)}}^T} \notag\\
&=P_m-K_{(m+1)}h_{(m+1)}P_m \notag \\
&=P_m(I-K_{(m+1)}h_{(m+1)})\end{align}
\]
第\(m+1\)次的最小二乘估计:
\[\hat \theta_{(m+1)}=\hat \theta_m+K_{(m+1)} ({z_{(m+1)}-h_{(m+1)}\hat \theta_m)}
\]
精度停机准则:
\[max_{\forall i }\begin{vmatrix} \frac{\hat \theta_{i(m+1)}-\hat \theta_{i(m)}}{\hat \theta_{i(m)}}\end{vmatrix}<\epsilon
\]
不错的博客文章:https://blog.csdn.net/qq_51065725/article/details/133680843
参考文献:https://zhuanlan.zhihu.com/p/677130045