能从布朗运动的股票中赚钱吗

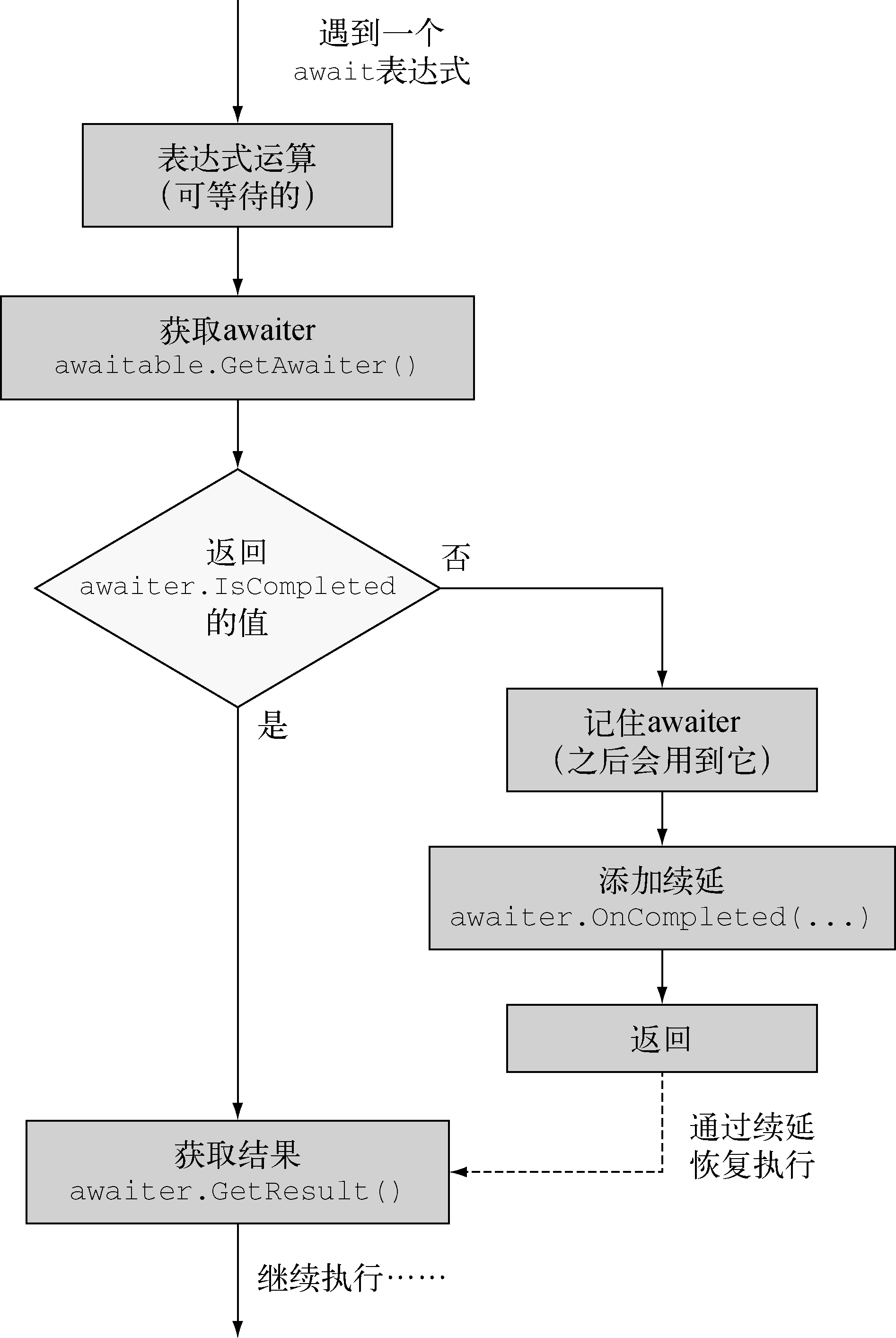
如果股票满足纯随机的布朗运动，采取赚到一定的钱就抛的策略，即不贪多。那么能否赚钱呢。如果是离散的情况，每个时刻以二分之一要么赚1要么跌1，可设出每个初始钱数到达止盈点的概率，用Markov链的方程计算，发现正好是0。实际上用鞅的观点看任何是鞅的随机过程都不可能凭空赚钱的。但下面用具体计算的方法算一下有上升趋势的布朗运动期望可赚多少。

对 \(d x=F d t+G d W \quad d W\) 理解为随机的扰动．\(W(t)\) 就是布朗运动（即满足 \(W(t)-W(s) \sim N(0, t-s))\) 有 Ito 链式法则：
\(d u(x, t)=u_t d t+u_x d x+\frac{1}{2} u_{x x} G^2 d t\) ，感性理解：把 \(d w\)看成 \(\sqrt{d t}\) ，对 \(u(x, t)\) 展开有 \(u(x, t)\)

\[\begin{aligned} u(x, t)= & u\left(x, t_1\right)+\frac{\partial u}{\partial x}\left(x-x_0\right)+\frac{\partial u}{\partial t}\left(t-t_0\right)+\frac{\partial^2 u}{\partial x \partial t}\left(x-x_0\right)\left(t-t_0\right) \\ & +\frac{1}{2} \frac{\partial^2 u}{\partial x}\left(x-x_0\right)^2+\frac{1}{2} \frac{\partial^2 u}{\left(\partial t^2\right.)}\left(t-t_0\right)^2+\cdots \cdot \end{aligned} \]

忽略 \(d t\) 高阶项 \((d x)^2\) 里有一个 \((d w)^2\) 成了 \(d t\) 。
于是假设股票满足：\(\quad d x=\mu d t+\sigma d w \quad\) 设 \(u=u(x)\)

\(u(x(T))-u(x(0))=\int_0^T u_x(\mu \ dt+G dW)+\frac{1}{2} U_{x x} \sigma^2 d t\)

若限定的范围为 \([0, M]\)

\(\tau\) 一个随机变量代表撞到 0 或M的时间令 \(T=\tau\) 并两边取期望, \(dW\) 会消失

\[E(u(x(T)))-U(x(0))=\int_0^T u_x(\mu \ dt)+\frac{1}{2} U_{x x} \sigma^2 d t \]

若u满足 \(\mu \frac{d u}{d x}+\frac{1}{2} \sigma^2\frac{d^2u}{(dx)^2}=0\) 则 \(E(u(x(\tau)))=u(x(0))\)
\(X(0)\) 为初始价格，如果再有 \(u(M)=1 \ \ \ u(0)=0\) ，则
\(u(x(\tau))=1 \text{ or }0\) 代表达不达到盈利扡点。即 \(E(u(x(\tau)))\) 为胜利的概率，解上述 ODE有

\[ \]

\[u(x)=\frac{e^{-\frac{2 \mu}{\sigma^2} x}-1}{e^{-\frac{2 \mu}{\sigma^2} M}-1} \]

特别地，\(\mu=0\) 时 \(u=\frac{X}{M}\)
期望

\[\frac{X}{M}(M-X(0))+\left(1-\frac{X}{M}\right)(-X(0))=0 \]