\[\newcommand{\D}[1]{\frac{\partial}{\partial #1}}
\newcommand{\DD}[2]{\frac{\partial^2}{\partial #1\partial #2}}\newcommand{GG}{g_{k}^{i}(x,s)g_{k}^{j}(x,s)}
\]
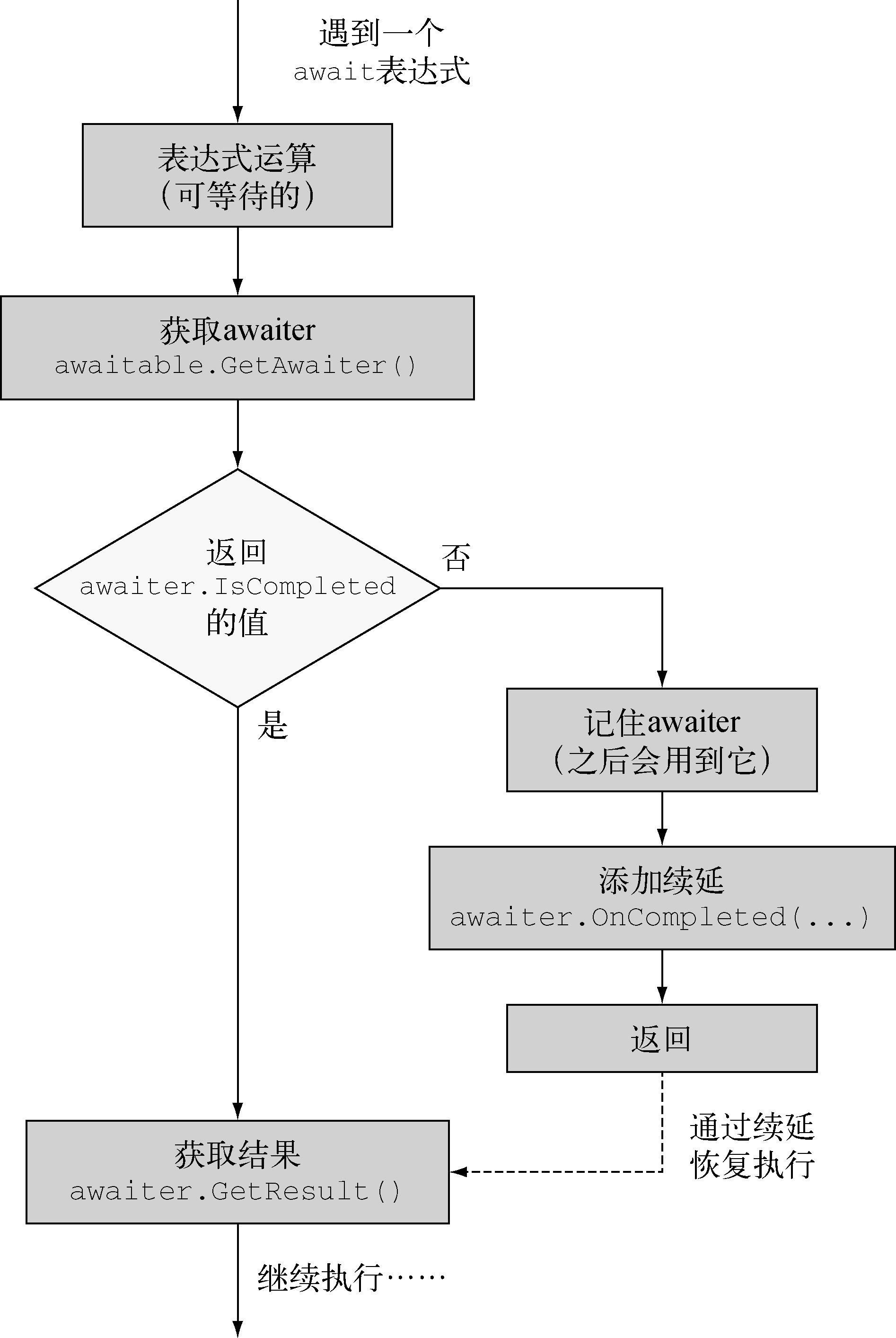
Diffusion Model中,在score matching 的流派中,我们是通过神经网络估计 \(\nabla_x \log p(x)\) 来从高斯分布中还原原来的图像分布,这就涉及到原扩散随机微分方程的逆向时间方程,即reverse-time SDE。下面从Ito公式开始推导reverse-time SDE的形式。其中重要的工具是kolmogorov于1930年提出的kolmogorov前向和后向方程
现有SDE
\[dx=f(x,t)dt+g(x,t)dW
\]
即
\[dx^i = f^i(\mathbf{x}, t) \, dt + \sum_{j=1}^n g_j^i(\mathbf{x}, t) \, dW^j, \quad i = 1, 2, \ldots, n.
\]
定义算子\(G\)
\[(G_th)(x)=\sum_{i}f^{i}(x,t)\D{x^i}h(x)+\frac{1}{2}\sum_{ijk}g_{k}^{i}(x,t)g_{k}^{j}(x,t)\DD{x^i}{x^j}h(x)
\]
多维的Ito公式可写成
\[d\phi(\mathbf{X}_t, t) = \left( \frac{\partial \phi}{\partial t} + \sum_{i=1}^n f^i \frac{\partial \phi}{\partial x^i} + \frac{1}{2} \sum_{i,j,k} g_k^i g_k^j \frac{\partial^2 \phi}{\partial x^i \partial x^j} \right) dt + \sum_{i,j} g_j^{i} \frac{\partial \phi}{\partial x^i} dW^j.
\]
令 \(\phi=h(x)\) 和 \(t\) 无关 。写成积分形式取期望 \(dW\) 项消失。可得Dynkin公式
\[E^x(h(x_t))=h(x)+E^x(\int_s^t(G_uh)(x_u)du)
\]
\(E^x\) 代表初值\(x_s=x\)
下面一律 \(s\leq t\) 如果记算子 \(P_{st}\) 为
\[(P_{st} h)(x)=E^x(h(x_t))=\int p_{st}(y,x)h(y)dy
\]
其中 \(p_{st}(y,x)\) 是一个卷积核满足 \(\int p(y,x) dy=1\) 代表时间从 \(s\) 到 \(t\) 后由 \(x\) 转移到 \(y\) 的概率密度, 则有
\[(P_{st}h)(x)=h(x)+\int_s^tdu((P_{su}G_uh)(x_u)\tag{1})
\]
将 \(h(x)\) 移到左边,除以 \(t-s\) 求极限,再由 \(P_{ss}=id\) 得到
\[G_sh=\lim_{t\to s}\frac{P_{st}h-h}{t-s}\\
G_th=\lim_{s\to t}\frac{P_{st}h-h}{t-s}\\
G_t=\lim_{u\to 0}\frac{P_{t,t+u}-id}{u}\\
G_s=\lim_{u\to 0}\frac{P_{s-u,s}-id}{u}
\]
所以 \(G\) 也叫无穷小生成元((infinitesimal generator)
将第三式两边左乘 \(P_{st}\) ,得到 Kolmogorov forward equation
\[\frac{d}{dt}P_{st}=P_{st}G_t \tag{2}
\]
将第四式两边右乘 \(P_{st}\) ,得到 Kolmogorov backward equation
\[\frac{d}{ds}P_{st}=-G_sP_{st} \tag{3}
\]
写成展开成卷积的形式
\[\begin{gather*}
P_{st}G_th(x)=\int p_{st}(y,x)(\sum_{i}f^{i}(y,t)\D{y_i}h(y)+\frac{1}{2}\sum_{ijk}g_{k}^{i}(y,t)g_{k}^{j}(y,t)\DD{y_i}{y_j}h(y))dy\\
=-\sum_i\int_0^t\D{y_i}(p_{st}(y,x)f^{i}(y,t))h(y)dy+\frac{1}{2}\sum_{ijk}\int_0^t\DD{y_i}{y_j}(p_{st}(y,x)g_{k}^{i}(y,t)g_{k}^{j}(y,t))h(y)dy
\end{gather*}
\]
其中用到分部积分,之后去掉 \(h\) ,\((2)\) 将化为
\[\frac{\partial}{\partial t}p_{st}(y,x)=-\sum_i\frac{\partial}{\partial y^i}(p_{st}(y,x)f^{i}(y,t))+\frac{1}{2}\sum_{i,j,k}\frac{\partial^2}{\partial y^i\partial y^j}(p_{st}(y,x)g_{k}^{i}(y,t)g_{k}^{j}(y,t))\tag{4}
\]
到此写成了PDE形式,类似可将 \((3)\) 化为
\[-\frac{\partial}{\partial s}p_{st}(y,x)=\sum_i(\frac{\partial}{\partial x^i}p_{st}(y,x))f^{i}(x,s)+\frac{1}{2}\sum_{i,j,k}(\frac{\partial^2}{\partial x^i\partial x^j}p_{st}(y,x))g_{k}^{i}(x,s)g_{k}^{j}(x,s)\tag{5}
\]
这对应Anderson的 \((3.9)\) 但是好像他写错了,后面的 \((5.2)\) 才是对的
简记 \(p_t(x)=p_{0,t}(x,0)\) 根据 \((4)\) 有
\[\frac{\partial}{\partial s}p_{s}(x)=-\sum_i\frac{\partial}{\partial x^i}(p_s(x)f^{i}(x,s))+\frac{1}{2}\sum_{i,j,k}\frac{\partial^2}{\partial x^i\partial x^j}(p_s(x)g_{k}^{i}(x,s)g_{k}^{j}(x,s))
\]
综合 \((4)(5)\) 有
\[\frac{\partial}{\partial s}(p_{st}(y,x)p_{s}(x))\tag{6}=\\-\sum_i(\frac{\partial}{\partial x^i}p_{st}(y,x))f^{i}(x,s)p_{s}(x)-\frac{1}{2}\sum_{i,j,k}(\frac{\partial^2}{\partial x^i\partial x^j}p_{st}(y,x))g_{k}^{i}(x,s)g_{k}^{j}(x,s)p_{s}(x)\\-\sum_i\frac{\partial}{\partial x^i}(p_s(x)f^{i}(x,s))p_{st}(y,x)+\frac{1}{2}\sum_{i,j,k}\frac{\partial^2}{\partial x^i\partial x^j}(p_s(x)g_{k}^{i}(x,s)g_{k}^{j}(x,s))p_{st}(y,x)
\]
其中第一第三项
\[-\sum_i(\frac{\partial}{\partial x^i}p_{st}(y,x))f^{i}(x,s)p_{s}(x)-\sum_i\frac{\partial}{\partial x^i}(p_s(x)f^{i}(x,s))p_{st}(y,x)\\=-\sum\D{x^i}(p_s(x)f^{i}(x,s)p_{st}(y,x))
\]
\(\frac{1}{2}\) 的两项为
\[-\frac{1}{2}\sum_{i,j,k}(\frac{\partial^2}{\partial x^i\partial x^j}p_{st}(y,x))g_{k}^{i}(x,s)g_{k}^{j}(x,s)p_{s}(x)+\frac{1}{2}\sum_{i,j,k}\frac{\partial^2}{\partial x_i\partial x^j}(p_s(x)g_{k}^{i}(x,s)g_{k}^{j}(x,s))p_{st}(y,x)\\
=-\frac{1}{2}\sum_{i,j,k}(\frac{\partial^2}{\partial x^i\partial x^j}p_{st}(y,x))g_{k}^{i}(x,s)g_{k}^{j}(x,s)p_{s}(x)-\frac{1}{2}\sum_{i,j,k}\frac{\partial^2}{\partial x_i\partial x^j}(p_s(x)g_{k}^{i}(x,s)g_{k}^{j}(x,s))p_{st}(y,x)\\
-\sum_{i,j,k}\D{x^i}P_{st}(y,x)\D{x^j}(P_s(x)\GG)\\
+\sum_{i,j,k}\D{x^i}P_{st}(y,x)\D{x^j}(P_s(x)\GG)
+\sum_{i,j,k}\frac{\partial^2}{\partial x^i\partial x^j}(p_s(x)g_{k}^{i}(x,s)g_{k}^{j}(x,s))p_{st}(y,x)
\]
前三项合并为
\[-\frac{1}{2}\sum_{i,j,k}\DD{x^i}{x^j}(p_s(x)p_{st}(y,x)\GG)
\]
后两项为
\[\sum_i\D{x^i}(p_{st}(y,x)\sum_{j,k}\D{x^j}(p_s(x)\GG)
\]
设 \(\bar{f}\) 为
\[\bar{f^i}(x,s)=f^i(x,s)-\frac{1}{p_s(x)}\sum_{j,k}\D{x^j}(p_s(x)\GG)
\]
则 \((6)\) 化为
\[\frac{\partial}{\partial s}(p_{st}(y,x)p_{s}(x))=\\-\sum\D{x^i}(p_s(x)\bar{f^{i}}(x,s)p_{st}(y,x))-\frac{1}{2}\sum_{i,j,k}\DD{x_i}{x^j}(p_s(x)p_{st}(y,x)\GG)
\]
使用 Bayesian 公式
\[q_{ts}(x,y)=\frac{p_s(x)p_{st}(y,x)}{p_t(y)}
\]
其中 \(q\) 代表 \([s,t]\) 时间中 \(y\) 是从 \(x\) 走过来的概率密度 ,或者说逆转时间后 \(t\to s\) 间 \(y\) 走到 \(x\) 的概率
将所有 \(p_s(x)p_{st}(y,x)\) 换成 \(q_{ts}(x,y)p_t(y)\) 再把两边除以 \(p_t(y)\)
\[\frac{\partial}{\partial s}(q_{ts}(x,y))=\\-\sum\D{x^i}\bar{f^{i}}(x,s)q_{ts}(x,y)-\frac{1}{2}\sum_{i,j,k}\DD{x^i}{x^j}(q_{ts}(x,y)\GG)
\]
令一个逆向时间 \(\bar{s}=-s\) \(\bar{t}=-t\)
\[-\frac{\partial}{\partial \bar{s}}(q_{\bar{ts}}(x,y))=\\\sum\D{x^i}(-\bar{f^{i}}(x,s))q_{\bar{ts}(x,y)}-\frac{1}{2}\sum_{i,j,k}\DD{x^i}{x^j}(q_{\bar{ts}}(x,y)\GG) \tag{7}
\]
这和 \((4)\) 完全形式对应,于是可以重构一个逆向 SDE
\[dx=(-\bar{f}(x,\bar{t}))d\bar{t}+g(x,\bar{t})dW
\]
但是如果我们把初值设为 \(t\) 处的值并让时间正向流动(之前是时间和运动均是逆向,现在对应到时间正向但模拟原来过程逆向的运动)由于 \(dt=-d\bar{t}\)
\[dx=\bar{f}(x,t)dt+g(x,t)dW
\]
这就是reverse-time diffusion方程。
注:在Kolmogorov的原始表述中前后向方程的 \(x\) 一二阶导项的系数分别与随机过程的无穷小时间移动的期望和方差有关,正好在Ito SDE中对应了 \(f\) 和 \(g^2\)
参考文献:
-
Anderson, “Reverse-time diffusion equation models,” Stochastic
Process. Appl., vol. 12, no. 3, May pp. 313–326, 1982, url: https://
www.sciencedirect.com/science/article/pii/0304414982900515.
-
Evans SDE p107 (6)
-
GTM261 Probability and Stochastics p462 Infinitesimal generator 但是他假设 \(x\) 平稳,本文要将\(P_t\) 改为 \(P_{st}\) p39 Markov Kernel, 本文直接假设卷积核能写成概率密度,并属于\(C^2\)。
-
Kolmogorov Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung, Math. Ann.
104 (1931)