使用定时器的规避方法
为了避免定时器误差导致倒计时计算错误，可以采用一些规避方法，比如将倒计时被中断时的剩余时间记录下来，重新开启定时器时再将这个剩余时间加到新的计算中。同时，为了避免定时器延迟，可以在每次执行回调函数时，记录当前时间戳，再计算与上一次执行回调函数的时间差，来调整倒计时的时间。

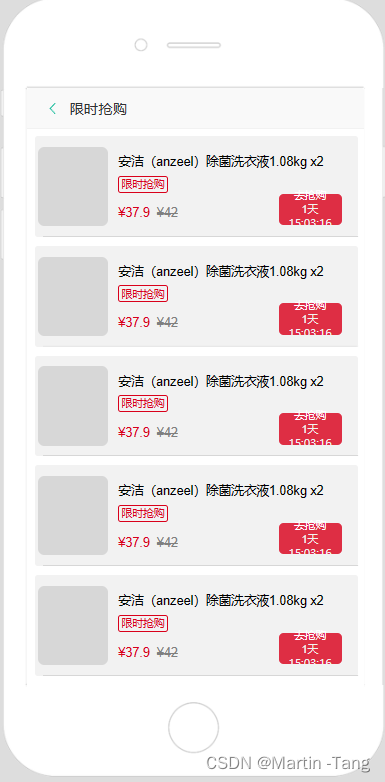
1.子组件<template><view class="time"><view class="red-box" >{{days>=10?days:'0'+days}}</view><view class="fz-12 color3" style="margin: 0 2px;">天</view><view class="red-box" >{{hours>=10?hours:'0'+hours}}</view><view class="fz-12 color3" style="margin: 0 2px;">时</view><view class="red-box">{{minutes>=10?minutes:'0'+minutes}}</view><view class="fz-12 color3" style="margin: 0 2px;">分</view><view class="red-box">{{seconds>=10?seconds:'0'+seconds}}</view><view class="fz-12 color3" style="margin: 0 2px;">秒</view></view>
</template><script>export default {props: {targetDate: {type: String,required: true}},data() {return {countdownInterval: null,days: 0,hours: 0,minutes: 0,seconds: 0};},mounted() {this.startCountdown();},beforeDestroy() {clearInterval(this.countdownInterval);},methods: {startCountdown() {this.updateCountdown(); // 先立即更新一次this.countdownInterval = setInterval(() => {this.updateCountdown();}, 1000);},updateCountdown() {const now = new Date();const target = new Date(this.targetDate);const duration = Math.max(0, target - now) / 1000;this.days = Math.floor(duration / 86400);this.hours = Math.floor((duration % 86400) / 3600);this.minutes = Math.floor((duration % 3600) / 60);this.seconds = Math.floor(duration % 60);if (duration <= 0) {clearInterval(this.countdownInterval);this.$emit('countdownFinished'); // 触发倒计时结束事件}}}};
</script>
<style lang="scss" scoped>.time {margin-top: 4rpx;display: flex;color: #ff0000;font-size: 22rpx;text-align: center;align-items: center;.red-box {font-size: 22rpx;}}.color3{color: #ff0000;font-size: 22rpx;}
</style>