算法通关村第十九关：白银挑战-动态规划高频问题

白银挑战-动态规划高频问题

1. 最少硬币数

LeetCode 322
https://leetcode.cn/problems/coin-change/description/

思路分析

尝试用回溯来实现
假如coins=[2,5,7]，amount=27，求解过程中，每个位置都可以从[2,5,7]中选择，因此可以逐步将所有情况枚举出来，然后再找到要求的最少硬币数，图示如下：
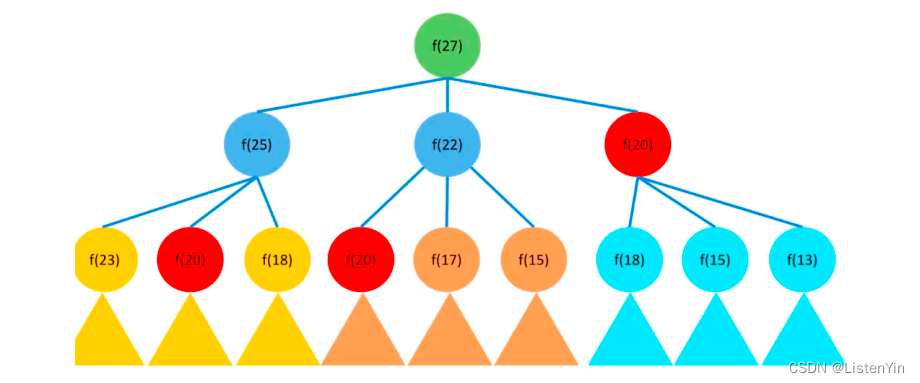
在这里插入图片描述

通过上面的图，发现 f[20] 等已经存在多次重复计算了，存在大量重复计算的问题，效率低。

尝试用贪心来实现
直觉告诉我们尽量使用大的，假如coins=[2,5,7]，amount=27
先连续用 7+7+7=21，剩下6用2+2+2=6，一共 7+7+7+2+2+2=27，共使用了6枚硬币
但我们可以使用 7+5+5+5+5=27，使用5枚硬币就够了
贪心的思路不能解决本题

尝试用DP来实现
使用DP能同时满足效率和准确性

设状态f(x)，最少用f(x)枚硬币能拼出x
建立数组arr，索引表示的是 amount，表示最少需要arr[i]个硬币能拼出来
其中有些位放的是M，表示就是不能拼出来的意思

coins = [1,2,5] 时
在这里插入图片描述

coins = [2,5,7] 时
在这里插入图片描述

以coins=[2,5,7]，详细分析一步步实现DP

第一步：确定状态和子问题

状态
f(x)，最少用f(x)枚硬币能拼出x

子问题
先看最后一步，从后向前找递归

  • 最优策略K枚硬币，a1, a2, … ak 面值加起来是27
  • 除掉最后一枚硬币ak，前面硬币加起来面值就是 27-ak
  • ak一定是 2,5,7 中的一枚
    • 如果ak=2，f(27)=f(25)+1
    • 如果ak=5，f(27)=f(22)+1
    • 如果ak=7，f(27)=f(20)+1
  • f(27)=min(f(25),f(22),f(20))+1

在这里插入图片描述

f(27)=min(f(25),f(22),f(20))+1
接下来，根据递归的思想再去算 f(25),f(22),f(20)…

其中f(6)=min(f(4),f(1),f(-1))+1
f(1)和f(-1)不满足要求，需要设置为正无穷
f(4)=2，f(6)=2+1=3

总结：递推要从右向左，计算要从左向右

第二步：确定状态转移方程

子问题确定之后，状态转移方程也基本确定了
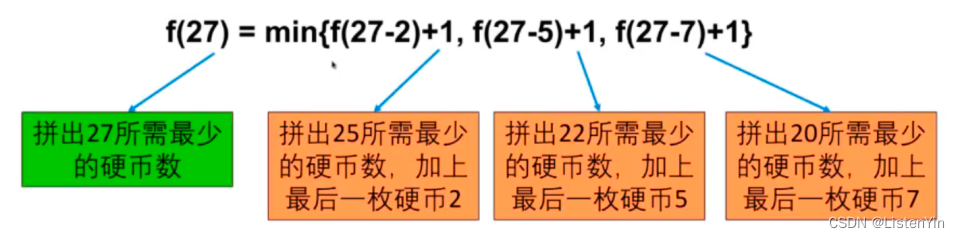
在这里插入图片描述

f(x) = min(f(x-2), f(x-5), f(x-7)) + 1

第三步：确定初始条件和边界

初始条件 f(0) = 0
如果不能拼出x，就定义f(x)为正无穷

注意溢出问题：
如果不能拼定义为正无穷，可能存在溢出问题
可以用amount来代替正无穷

第四步：按顺序计算

执行状态转移方程 f(x) = min(f(x-2), f(x-5), f(x-7)) + 1 对数组进行计算
递推要从右向左，计算要从左向右

第五步：代码实现

第一版代码

# 伪代码
def coin(coins, amount):max_num = amount + 1dp = [max_num] * (amount + 1)dp[0] = 0for i in range(amount + 1):if check(i):dp[i] = min(dp[i - coins[0]], dp[i - coins[1]], dp[i - coins[2]]) + 1return dp[amount] if dp[amount] < max_num else -1def check(i, coins):# 这里要保证 i - coins[i] 大于0# 这里还要保证不越界，写起来比较复杂，我们理解功能即可pass

第二版代码

# 伪代码
def coin(coins, amount):max_num = amount + 1dp = [max_num] * (amount + 1)dp[0] = 0for i in range(amount + 1):if check(i):dp[i] = min(dp[i], dp[i - coins[0]] + 1)dp[i] = min(dp[i], dp[i - coins[1]] + 1)dp[i] = min(dp[i], dp[i - coins[2]] + 1)return dp[amount] if dp[amount] < max_num else -1def check(i, coins):# 这里要保证 i - coins[i] 大于0# 这里还要保证不越界，写起来比较复杂，我们理解功能即可pass

如果 coins[] 数组比较大，if判断就非常长，考虑价格循环解决，最终代码实现如下

第三版代码

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:max_num = amount + 1dp = [max_num] * (amount + 1)dp[0] = 0for i in range(1, amount + 1):for j in range(len(coins)):if i - coins[j] >= 0:dp[i] = min(dp[i], dp[i - coins[j]] + 1)return dp[amount] if dp[amount] < max_num else -1

总结一下求最值型DP的步骤

  1. 确定状态和子问题。
    从最后一步开始（最优策略中使用的最后一枚硬币ak）推导f(n)与子问题之间的关系，然后将其化成子问题（最少的硬币拼出更小的面值27-ak)

  2. 通过状态，可以得到状态转移方程 f(x) = min(f(x-2), f(x-5), f(x-7)) + 1

  3. 处理初始条件和边界问题。f[0]=0，其他如果不能拼出来标记为 f(x)=正无穷

  4. 从小到大开始计算。这里就是从 f(0),f(1),f(2)…向后计算

2. 最长连续递增子序列

LeetCode 674
https://leetcode.cn/problems/longest-continuous-increasing-subsequence/description/

思路分析

不用动态规划也能解决，例如前面介绍的滑动窗口就可以

动态规划解决

在这里插入图片描述

第一步：分析状态和子问题
状态 f(i) ，以a[i]结尾的最长连续上升子序列的长度

最后一个元素a[j]，存在两种情况

  1. a[j]<=a[j-1]，f[j]=1 (a[j]<=a[j-1] or j=0)
  2. a[j]>a[j-1]，f[j] = f[j-1]+1 (j>0且a[j]>a[j-1])

第二步：转移方程
f[j]=1 a[j]<=a[j-1] or j=0)
f[j] = f[j-1]+1 j>0且a[j]>a[j-1]

第三步：初始条件和边界
f[j]=1 a[j]<=a[j-1] or j=0)
f[j] = f[j-1]+1 j>0且a[j]>a[j-1]

第四步：按照顺序计算
和硬币组合不一样，答案为 max([f(0), f(1), f(2), … ,f(n-1)])

代码实现

class Solution:def findLengthOfLCIS(self, nums: List[int]) -> int:# 动态规划arr = [1] * len(nums)for i in range(1, len(nums)):if nums[i] > nums[i-1]:arr[i] = arr[i-1] + 1return max(arr)

3. 最长递增子序列

LeetCode 300
https://leetcode.cn/problems/longest-increasing-subsequence/description/、

思路分析

本题与上一题 LeetCode 674 的区别：没有说子序列元素一定是连续的

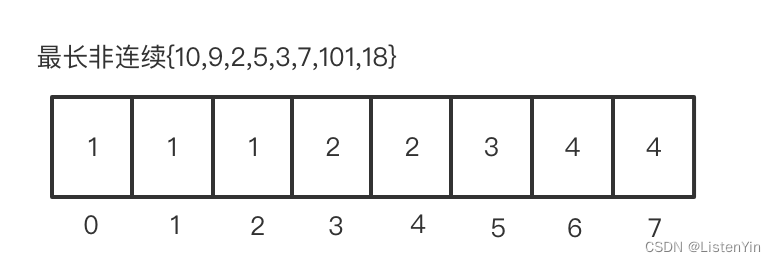
在这里插入图片描述

使用DP解决问题的方法

第一步：确定状态和子问题
状态f(x) 第x个元素的最长递增子序列长度，求以a[x]结尾的最长上升子序列

子问题：
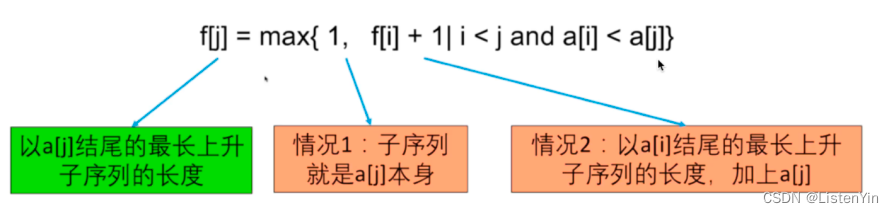
情况1：最长上升子序列为 { a[j] }，f[j] = 1
情况2：最长上升子序列大于1
0<=i<j，a[j]>a[i]，f[j] = f[i]+1
在这里插入图片描述

因为不确定最优策略中a[j]前一个元素a[i]是哪一个，需要枚举每个i，求以a[j]结尾的最长上升子序列
在这里插入图片描述

第二步：初始条件和边界
f[0] = 1
情况2必须满足
1.0<=i<j
2. a[j]>a[i]

第三步：计算顺序
计算 f[0],f[1],…,f[n-1]
答案就是这些数中最大的那个

代码实现

class Solution:def lengthOfLIS(self, nums: List[int]) -> int:# 动态规划arr = [1] * len(nums)for i in range(1, len(nums)):for j in range(i):if nums[i] > nums[j]:arr[i] = max(arr[j] + 1, arr[i])return max(arr)

class Solution:def lengthOfLIS(self, nums: List[int]) -> int:# 动态规划dp = []for i in range(len(nums)):dp.append(1)for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[j] + 1, dp[i])return max(dp)

4. 最少完全平方数

LeetCode279
https://leetcode.cn/problems/perfect-squares/description/

思路分析

手动画一下
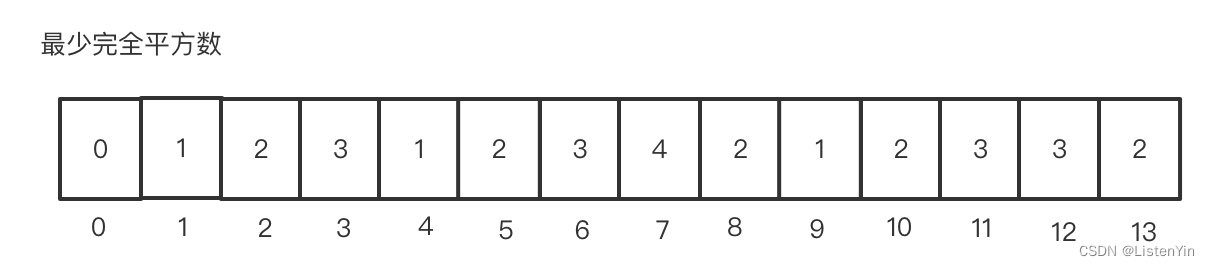
在这里插入图片描述

使用DP来实现

第一步：确定状态和子问题
状态：f[i] i最少被分成几个完全平方数之和
子问题：参考硬币的问题，f[i] = min(f[i-j*j]+1, f[i]) 1<=j<i^0.5

第二步：状态转移方程
f[i] = min(f[i-j*j]+1, f[i]) 1<=j<i^0.5

第三步：初始和边界条件
f[0] = 0

第四步：计算顺序
计算 f[0],f[1],…,f[n-1],f[n]
答案就是f[n]

代码实现

class Solution:def numSquares(self, n: int) -> int:dp = [0]for i in range(1, n + 1):dp.append(i)for j in range(1, int(i**0.5) +1):dp[i] = (min(dp[i-j**2]+1, dp[i] ))return dp[n]

5. 再论青蛙跳

LeetCode 55
https://leetcode.cn/problems/jump-game/description/

思路分析
典型的贪心问题，下面从动态规划的角度来分析解题

  1. 状态和子问题
    状态：f[x] 能否跳跃值x
    子问题：可以跳到j，j可以跳到i
  2. 状态转移方程
    f[i] = True | 0<=j<i and f[j] and a[j]>=i-j
  3. 初始和边界条件
    f[0] = True
  4. 顺序
    计算 f[0],f[1],…,f[n-1] 答案就是f[n-1]

代码实现

class Solution:def canJump(self, nums: List[int]) -> bool:# 动态规划bp = [False] * len(nums)bp[0] = Truefor i in range(1, len(nums)):for j in range(i):if bp[j] and nums[j] >= i - j:bp[i] = Truereturn bp[-1]

注：动态规划可以实现，但在LeetCode上，运行超出时间限制

6. 解码问题

LeetCode 91
https://leetcode.cn/problems/decode-ways/description/

思路分析

  1. 状态和子问题
    状态：f[i] 以a[i]结尾，可以有多少种解码方式
    子问题：
    最后一个字母的解码有两种情况
    情况1：1个数字解码 a[i]对应一个字母，f[i] = f[i-1]
    情况2：2个数字解码 a[i-1]a[i]对应一个字母，f[i] = f[i-2]

    综上，f[i] = f[i-1](条件:a[i]可以对应一个字母) + f[i-2](条件:a[i-1]a[i]可以对应一个字母)

  2. 状态转移方程
    f[i] = f[i-1](条件:a[i]可以对应一个字母) + f[i-2](条件:a[i-1]a[i]可以对应一个字母)

  3. 初始和边界条件
    初始条件f[0] = 1 理解为空串，有一种解码方式
    边界条件：i = 1，只看最后一个数字就行了

  4. 顺序
    计算 f[0],f[1],…,f[n-1] 答案就是f[n]

代码实现

class Solution:def numDecodings(self, s: str) -> int:n = len(s)dp = [0] * (n + 1)dp[0] = 1for i in range(1, n + 1):if s[i - 1] != '0':dp[i] += dp[i - 1]if i > 1 and 10 <= int(s[i - 2]) * 10 + int(s[i - 1]) <= 26:dp[i] += dp[i - 2]return dp[len(s)]

7. 路径中存在障碍物

LeetCode 63
https://leetcode.cn/problems/unique-paths-ii/description/

我们在路径部分介绍了多种路径的问题
本专题有个重要的拓展，加入网格中存在障碍物怎么办?

本题是在 LeetCode 62 的基础上，如果中间某个位置存在障碍物，那一共有多少种路径。

示例
输入    obstacleGrid = [[0,0,0], [0,1,0], [0,0,0]]
输出    2
解释    3x3 网格的正中间有一个障碍物从左上角到右下角一共有2条不同的路径1. 向右->向右->向下->向下2. 向下->向下->向右->向右

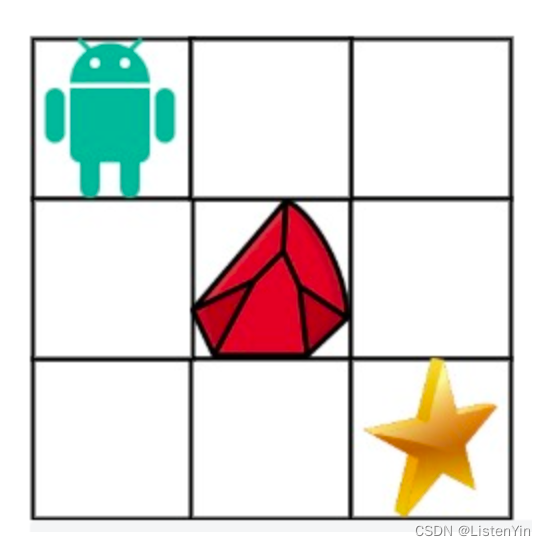
在这里插入图片描述

思路分析

处理方法不算复杂
设置没有障碍物的格子标记为0，有障碍物的格子标记为1
执行的时候如果当前位置dp[i][j] == 1时，直接跳过

代码实现

class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m = len(obstacleGrid)n = len(obstacleGrid[0])bp = [[0] * n for _ in range(m)]bp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0for i in range(m):for j in range(n):if obstacleGrid[i][j] == 1:bp[i][j] = 0elif i >= 1 and j >= 1:bp[i][j] = bp[i - 1][j] + bp[i][j - 1]elif i >= 1:bp[i][j] = bp[i - 1][j]elif j >= 1:bp[i][j] = bp[i][j - 1]return bp[-1][-1]

class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:# 滚动数组实现m = len(obstacleGrid)n = len(obstacleGrid[0])dp = [0] * ndp[0] = 1 if obstacleGrid[0][0] == 0 else 0for i in range(m):for j in range(n):if obstacleGrid[i][j] == 1:dp[j] = 0elif j - 1 >= 0 and obstacleGrid[i][j - 1] == 0:dp[j] += dp[j - 1]return dp[n - 1]

8. 滚动数组技巧

LeetCode 118
https://leetcode.cn/problems/pascals-triangle/description/
LeetCode 119
https://leetcode.cn/problems/pascals-triangle-ii/description/

杨辉三角
特点：每个元素嗾使其二维矩阵中左上方和右上方的元素之和，是一种对称结构
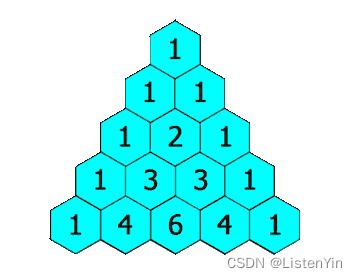
在这里插入图片描述

用二维数组表示
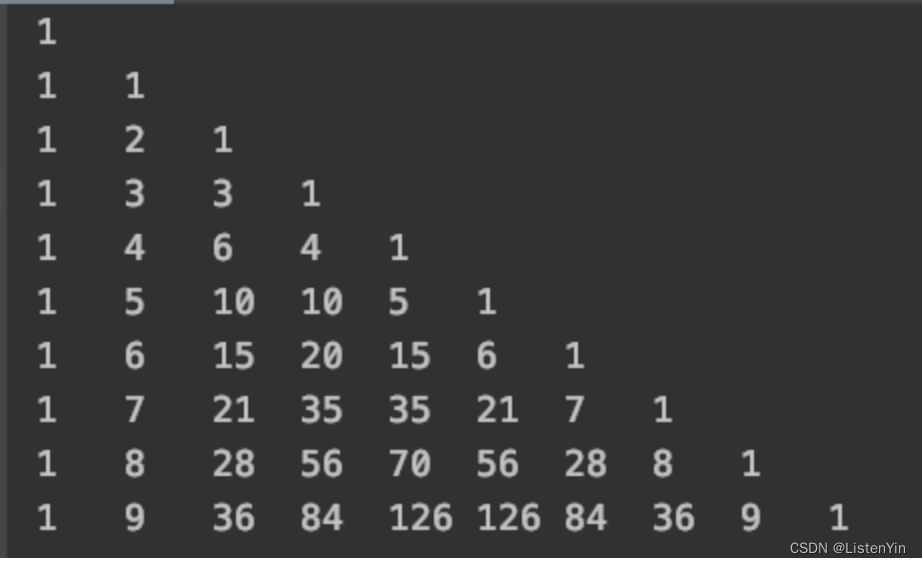
在这里插入图片描述

  • 每一行的最右侧和最左侧都是1
  • 前两行时1，第3行才开始有累加的问题
  • 每一行的元素数量与其行数一样

代码实现

LeetCode 119

class Solution:def getRow(self, rowIndex: int) -> List[int]:# 新建二维数组a = [[] for _ in range(rowIndex+1)]for i in range(rowIndex+1):# 确定每一行数组a[i] = [0] * (i + 1)# 第1个和最后1个元素为1a[i][0] = 1a[i][i] = 1for i in range(rowIndex+1):# 从第3行开始if i >= 2:for j in range(1, len(a[i]) - 1):a[i][j] = a[i - 1][j - 1] + a[i - 1][j]return a[-1]

思路分析

如果要求只能使用O(n)空间实现呢？可以使用上面提到的滚动数组来做

a[i][j] = a[i-1][j-1] + a[i-1][j]

存在问题：计算dp[i]的时候，需要上一轮的dp[i-1]，但是这个值已经被覆盖了
例如下图中的 3 需要使用上一轮的2和1进行相加，但是此时2已经覆盖成3了，所以仅靠一个一维数组无法解决问题

在这里插入图片描述

可以使用两个数组，也是O(n)空间，使用两个数组来进行轮换交流
如下图所示，黑色代表上一轮的结构，红色表示当前轮更新的结果
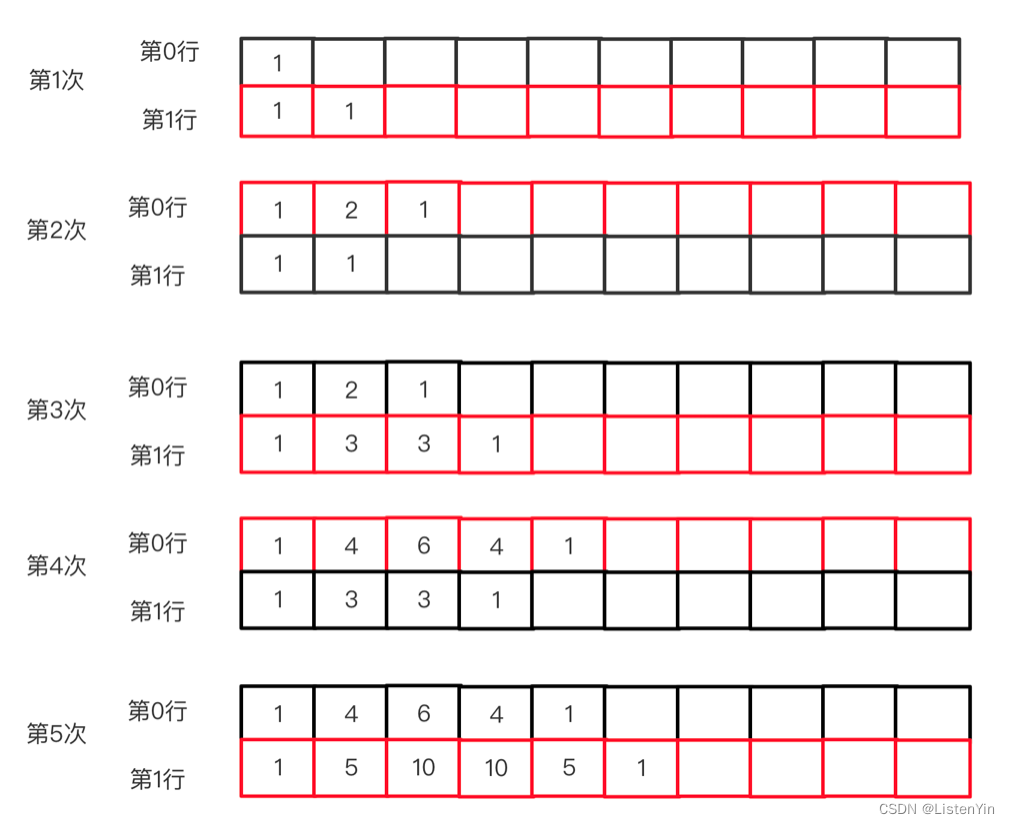
在这里插入图片描述

代码实现

LeetCode 119

class Solution:def getRow(self, rowIndex: int) -> List[int]:# 滚动数组，两个一维数组pre = []cur = []for i in range(rowIndex+1):for j in range(i + 1):if j == 0 or i == j:cur.append(1)else:cur.append(pre[j - 1] + pre[j])pre = curcur = []return pre

思路分析

如果只能使用一个一维数组来完成，该怎么做呢？

观察 cur[j] = pre[j-1] + pre[j]，第 j 项的计算与上一行第 j-1 项和第 j 项有关

可以倒着算，就没有影响了，先计算第 j 项，再计算第 j-1 项，这样计算第 j 项时，第 j-1 项还是上一行的值
cur[j] = cur[j-1] + cur[j]

# 两个二维数组
for j in range(i + 1):if j == 0 or i == j:cur.append(1)else:cur.append(pre[j - 1] + pre[j])

变为

# 一个二维数组
for j in range(i, -1, -1):if j == 0 or i == j:arr[j] = 1else:arr[j] = arr[j - 1] + arr[j]

代码实现

LeetCode 119

class Solution:def getRow(self, rowIndex: int) -> List[int]:# 滚动数组，一个一维数组arr = []for i in range(rowIndex+1):arr.append(0)for j in range(i, -1, -1):if j == 0 or i == j:arr[j] = 1else:arr[j] = arr[j - 1] + arr[j]return arr

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/107782.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

iwebsec靶场 文件包含漏洞通关笔记3-session文件包含

iwebsec靶场 文件包含漏洞通关笔记3-session文件包含

目录 1.打开靶场 2.源码分析 &#xff08;1&#xff09;session文件包含漏洞的的工作原理 &#xff08;2&#xff09;sessionstart()做了哪些初始化工作 3.获取session文件位置 4.向session写入webshell 5.访问webshell 1.打开靶场 iwebsec 靶场漏洞库iwebsechttp://iw…
阅读更多...
【Blender】Blender入门学习

【Blender】Blender入门学习

目录 0 参考视频教程0.1 Blender理论知识0.2 Blender上手实践0.3 FBX模型导入Unity 1 Blender的窗口介绍1.1 主界面1.2 模型编辑窗口 2 Blender的基本操作2.1 3D视图的平移2.2 3D视图的旋转2.3 3D视图的缩放2.4 修改快捷键2.5 使物体围绕选择的物体旋转2.6 四视图的查看2.7 局部…
阅读更多...
遥遥领先的内存函数

遥遥领先的内存函数

目录 ​编辑 函数介绍 1.1 strlen 1.2 strcpy 1.3 strcmp 1.4 strcat 1.5 strstr 2.1 memcpy 2.2 memmove 2.3 memcmp 函数实现 1.1 strlen 1.2 strcpy 1.3 strcmp 1.4 strcat 1.5 strstr 2.1 memcpy 2.3 memcmp 函数介绍 1.1 strlen size_t strlen ( const char *…
阅读更多...
猫头虎的技术笔记：Spring Boot启动报错解决方案

猫头虎的技术笔记：Spring Boot启动报错解决方案

&#x1f337;&#x1f341; 博主猫头虎&#xff08;&#x1f405;&#x1f43e;&#xff09;带您 Go to New World✨&#x1f341; &#x1f984; 博客首页——&#x1f405;&#x1f43e;猫头虎的博客&#x1f390; &#x1f433; 《面试题大全专栏》 &#x1f995; 文章图文…
阅读更多...
4.3.3 【MySQL】Redundant行格式

4.3.3 【MySQL】Redundant行格式

现在我们把表demo 的行格式修改为 Redundant &#xff1a; 为了方便大家理解和节省篇幅&#xff0c;我们直接把表 demo 在Redundant 行格式下的两条记录的真实存储数据提供出来&#xff0c;之后我们着重分析两种行格式的不同即可。 下边我们从各个方面看一下 Redundant 行格式有…
阅读更多...
市场开始复苏，三星传调涨内存芯片高达20% | 百能云芯

市场开始复苏，三星传调涨内存芯片高达20% | 百能云芯

随着行动内存芯片市场迹象显示出复苏迹象&#xff0c;并且最早在第四季度供不应求&#xff0c;三星电子已宣布将提高动态随机存取存储器&#xff08;DRAM&#xff09;和NAND闪存芯片的价格&#xff0c;幅度达到10%~20%。 韩国经济日报报道&#xff0c;知情人士透露&#xff0c;…
阅读更多...
Day57|leetcode 647. 回文子串、516.最长回文子序列

Day57|leetcode 647. 回文子串、516.最长回文子序列

leetcode 647. 回文子串 题目链接&#xff1a;647. 回文子串 - 力扣&#xff08;LeetCode&#xff09; 视频链接&#xff1a;动态规划&#xff0c;字符串性质决定了DP数组的定义 | LeetCode&#xff1a;647.回文子串_哔哩哔哩_bilibili 题目概述 给你一个字符串 s &#xff0c;…
阅读更多...
30岁游戏服务端开发者的独立游戏梦想，你不敢想的事他都做了！

30岁游戏服务端开发者的独立游戏梦想，你不敢想的事他都做了！

小的时候家里就是开电动游戏厅的&#xff0c;所以我从小就喜欢玩游戏&#xff0c;尤其是那些有创意和故事性的游戏。 我梦想着有一天能够制作出自己的游戏&#xff0c;让更多的人享受到游戏带来的乐趣。 为了实现这个梦想&#xff0c;我选择了学习计算机科学&#xff0c;并在毕…
阅读更多...
cpu温度监测 Turbo Boost Switcher Pro for mac最新

cpu温度监测 Turbo Boost Switcher Pro for mac最新

Turbo Boost Switcher Pro是一款Mac电脑上的应用程序&#xff0c;旨在帮助用户控制和管理CPU的Turbo Boost功能。Turbo Boost是Intel处理器中的一项技术&#xff0c;可以在需要更高性能时自动提高处理器的频率。然而&#xff0c;这可能会导致电池消耗更快和温度升高。 以下是T…
阅读更多...
用python实现基本数据结构【01/4】

用python实现基本数据结构【01/4】

说明 如果需要用到这些知识却没有掌握&#xff0c;则会让人感到沮丧&#xff0c;也可能导致面试被拒。无论是花几天时间“突击”&#xff0c;还是利用零碎的时间持续学习&#xff0c;在数据结构上下点功夫都是值得的。那么Python 中有哪些数据结构呢&#xff1f;列表、字典、集…
阅读更多...
64、使用 Spring WebFlux 的 WebClient 整合第三方Restful服务

64、使用 Spring WebFlux 的 WebClient 整合第三方Restful服务

这节的要点&#xff1a; 就是弄两个项目 &#xff0c; 从 端口9090 这个项目&#xff0c;通过 webClient&#xff0c; 去访问 端口8080 的项目&#xff0c;并获取8080项目的数据。 ★ RESTful客户端的两种方式 - 应用基于传统的Spring MVC框架&#xff0c;此时考虑使用RestTe…
阅读更多...
K线学习001-早晨之星1

K线学习001-早晨之星1

K线定义 早晨之星&#xff0c;顾名思义&#xff1a;就是在太阳尚未升起的时候&#xff0c;黎明前最黑暗的时刻&#xff0c;一颗明亮的启明星在天边指引着那些走向光明的夜行人&#xff0c;前途当然看好。 早晨之星&#xff0c;即预示着跌势将尽&#xff0c;大盘处于拉升的前夜&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023