食用指南：本文在有C基础的情况下食用更佳

🔥这就不得不推荐此专栏了：C语言

♈️今日夜电波：ルミネセンス—今泉愛夏

1:01 ━━━━━━️💟──────── 5:05
🔄 ◀️ ⏸ ▶️ ☰

💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍

☸️一、前置知识：两种调整方法

向上调整方法

向下调整方法

✡️二、堆排序

堆排序的思想

记住一个公式！（非常重要！！！）

代码实现

🔯三、TOP-K问题

什么是TOP-K问题？

基本思路

🌰

☸️一、前置知识：两种调整方法

向上调整方法

堆的向上调整方法将新插入的节点从下往上逐层比较，如果当前节点比其父节点大（或小，根据是大根堆还是小根堆），则交换这两个节点。一直向上比较，直到不需要交换为止。这样可以保证堆的性质不变。

具体步骤如下：

1.将新插入的节点插入到堆的最后一位。

2.获取该节点的父节点的位置，比较该节点与其父节点的大小关系。

.如果该节点比其父节点大（或小，根据是大根堆还是小根堆），则交换这两个节点。

4.重复步骤2-3，直到不需要交换为止，堆的向上调整完成。

堆的向上调整的时间复杂度为O(logn)，其中n为堆的大小。

一图让你了解~（以大堆为例）

实现如下：

void swap(HPDataType* s1, HPDataType* s2)
{HPDataType temp = *s1;*s1 = *s2;*s2 = temp;
}void Adjustup(HPDataType* a, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent])//建大堆，小堆则<{swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

向下调整方法

堆的向下调整方法是指将某个节点的值下放至其子节点中，以维护堆的性质的过程。

假设当前节点为 i，其左子节点为 2i+1，右子节点为 2i+2，堆的大小为 n

则向下调整的步骤如下：

从当前节点 i 开始，将其与其左右子节点中较小或较大的节点比较，找出其中最小或最大的节点 j。
如果节点 i 小于等于（或大于等于，取决于是最小堆还是最大堆）节点 j，则说明它已经满足堆的性质，调整结束；否则，将节点 i 与节点 j 交换位置，并将当前节点 i 更新为 j。
重复执行步骤 1 和步骤 2，直到节点 i 没有子节点或已经满足堆的性质。

一图让你了解~（以大堆为例）

实现如下：

void swap(HPDataType* s1, HPDataType* s2)
{HPDataType temp = *s1;*s1 = *s2;*s2 = temp;
}void Adjustdown(HPDataType* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child])//找出两个孩子中较大的那个，此为大堆，如果要实现小堆则 改 >{++child;}if (a[child] > a[parent])//此为大堆，如果要实现小堆则 改 >{swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}

✡️二、堆排序

堆排序的思想

将待排序的序列构建成一个大根堆或小根堆，然后将堆顶元素与堆底元素交换，再重构堆，重复操作直到有序。堆排序的时间复杂度为O(nlogn)，空间复杂度为O(1)。算是一种较为高效的排序方法。

具体的实现步骤如下：

构建最大堆或最小堆。（建大堆排升序，建小堆排降序）
将堆顶元素（最大或最小值）与堆底元素交换。
从堆顶开始逐级向下调整堆，保证每个节点都符合堆的性质。
重复步骤2和步骤3，直到整个序列有序。

通常而言我们用的都是向下调整法来建堆以及排序，为什么呢？

向下调整法具有较好的时间复杂度：与向上调整法相比，向下调整法的时间复杂度更低，因为向下调整法只需要考虑每个非叶子节点的子树是否满足堆性质，而向上调整法需要考虑每个节点到根节点是否满足堆性质，时间复杂度较高。

记住一个公式！（非常重要！！！）

$parent=(n - 1 - 1) / 2$

这个公式是用来干什么的呢？用来找第一个有叶子节点的父节点的！

一图让你了解~

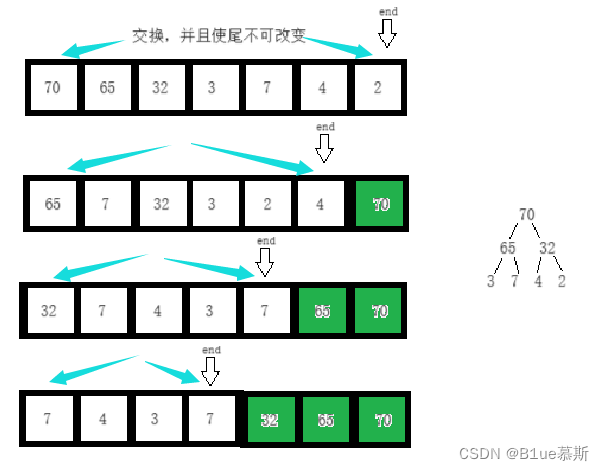
你可能有一个疑惑，我们这样建堆的意义是什么？答案是我们要将所有节点的左子树以及右子树都建成一个我们需要的堆（建大堆排升序，建小堆排降序）。这样做的意义是：让堆顶的元素在同最后一个堆的元素进行调换位置后，能够仅仅通过一次向下调整，（以大堆为例）就能让堆的最大元素排到队尾，并且不打乱顺序！！！

在理解了怎么建堆后，对于排序这件事实际上已经很简单了！

一图让你了解~

代码实现

void HeapSort(int* a, int n)//整体时间复杂度为nlog(n)
{//建大堆排升序，建小堆排降序//用的都是向下调整法来建堆以及排序//这里演示升序，如果要降序则修改向下调整法中的 > 变为 < ,使得建立的为小堆，并且后面的排序也将为降序！//建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--)//注意这里的i表示为第一个有叶子结点的父节点{Adjustdown(a, n, i);}//排序int end = n - 1;while (end > 0){swap(&a[0], &a[end]);Adjustdown(a, end, 0);--end;}}

🔯三、TOP-K问题

什么是TOP-K问题？

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决。

基本思路

        1. 用数据集合中前K个元素来建堆
                前k个最大的元素，则建小堆
                前k个最小的元素，则建大堆
        2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

                将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K 个最小或者最大的元素。

🌰

在随机的10000000个数据中找出前5大的数据。（通过文件建立以及读取实现）

该🌰的堆实现在这篇博文中：堆详解（点我跳转！！！）

实现如下：

void PrintTopK(const char* filename, int k)
{// 1. 建堆--用a中前k个元素建堆FILE* fout = fopen(filename, "r");if (fout == NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}// 前k个数建小堆for (int i = (k-2)/2; i >=0 ; --i){AdjustDown(minheap, k, i);}// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){// 替换你进堆minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");free(minheap);fclose(fout);
}// fprintf  fscanfvoid CreateNDate()
{// 造数据int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}int main()
{//CreateNDate();PrintTopK("data.txt", 5);return 0;
}

感谢你耐心的看到这里ღ( ´･ᴗ･` )比心，如有哪里有错误请踢一脚作者o(╥﹏╥)o！