RSA:基于小加密指数的攻击方式与思维技巧-编程知识

零、前言

最近，发现自己做题思路比较混乱。总的来说，就是在各种方法之间很难适配到对应的题目。所以，写下这篇博客来记录这些区别。特别说明的是，这篇文章更偏向于解题，而不是讲解原理。考虑到两个点，在写下这篇博客时本人其实也才学习了近1个月的密码学，数学知识严重匮乏，不敢乱教与解析原理。其次，备战省赛在即没有充分多的时间让我去了解学习深层次的原理。所以这里只能够给出使用条件，也就是应用层面上的区分。

此外特别声明，该篇博客更多的偏向于个人学习使用，其次是帮助大家应用。再者也欢迎各位指出错误，与提出问题。本人会在能力范围内尽可能作答。

一、小加密指数爆破

小加密指数爆破是最为简单的求解方式。几乎遇到小加密指数都可以尝试一下。因为它使用条件最为简单：加密指数小。需要注意的是，又是时候我需要分析数据特征。例如分析出flag比较短，即密文c很小时。我们可以优先直接开e次方。这一技巧出现于FSCTF中，这能帮助我们剔除混淆视听的提示--干扰信息。

[FSCTF]RSA签到

from Crypto.Util.number import *
from secret import flag
m = bytes_to_long(flag)
assert m.bit_length()<150
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 3
c = pow(m, e, n)
kbits = 103
m = (m >> kbits) << kbits
Mod = getPrime(2048)
hint1 = (2019-2023*m) % Mod
hint2 = pow(2, 2023, Mod)
print('n =',n)
print('c =',c)
print('hint1 =',hint1)
print('hint2 =',hint2)
'''
n = 113369575322962228640839640796005129142256499725384495463316595604047079557930666699058024217561098997292782305151595366764483672240871690818579470888054811186902762990032505953330034837625667158114251720321766235335996441613828302393569643827293040591156144187232255906107532680524431761932215860898533224303
c = 42336544435252811021843650684098817755849747192874682997240960601474927692351510022965782272751339319782351146077580929125
hint1 = 23620186624579054670890922956929031966199853422018331906359817627553015939570302421768667351617160816651880338639432052134891008193969801696035505565684982786461527274477933881508678074157199742425764746919878452990468268098540220237611917321213668069666526658025737487539455262610713002399515462380573732082344497124344090365729168706760425585735014513373401622860196569544933971210142724734536588173957576667830667503151362930889494877201597267000737408071228466811160470759093928003064486766171850080985758351203536462206720715743059101285822169971058423075796415932349942113371706910521251120400151508125606778268
hint2 = 963121833542317369601573845406471251262548645428284526828835768327851746644612875378048462019053502788803516653832734212104068969204751285764221918179043624419894139984279754512017898273159626328827668380262481220865017731267802600915375183179264380651165421367773563947903391466768557089792263481734108493385146063258300495764165365295546337808852673629710735621386935094923561594142327134318905856137785813985574356271679918694447015294481691849341917432346559501502683303082591585074576786963085039546446281095048723669230856548339087909922753762884060607659880382812905450025751549153093939827557015748608
'''

思路：

通过肉眼观察，我们也能发现 密文(c) << 模数(n)。

import gmpy2
from Crypto.Util.number import *n = 113369575322962228640839640796005129142256499725384495463316595604047079557930666699058024217561098997292782305151595366764483672240871690818579470888054811186902762990032505953330034837625667158114251720321766235335996441613828302393569643827293040591156144187232255906107532680524431761932215860898533224303
c = 42336544435252811021843650684098817755849747192874682997240960601474927692351510022965782272751339319782351146077580929125
'''
print(n.bit_length())
print(c.bit_length())
n.bit_length() = 1024
c.bit_length() = 405
'''if (gmpy2.iroot(m, 3)[1]):print(gmpy2.iroot(m, 3)[0]) # m = 34852863801144743432974618956978703253885m = 34852863801144743432974618956978703253885
print(long_to_bytes(m)) # flag{sign_1n_RSA}

二、基于小加密指数的有限域开根

实际上，有限域上的开根并不需要有小加密指数的限制。指数当指数较低的时候运算速度会快一点。

有限域上的开根条件为：e | phi，且 e | 任意因子的欧拉函数。

[NCTF 2019]easyRSA

from flag import flage = 0x1337
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
n = p * qassert(flag.startswith('NCTF'))
m = int.from_bytes(flag.encode(), 'big')
assert(m.bit_length() > 1337)c = pow(m, e, n)
print(c)
# 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359

思路：

首先我们能够看到 e = 0x1337 < 0x10001,算是比较小的一个加密指数。因此我们考虑一些基于小加密指数的攻击。但是因为这里 e = 0x1337 虽然算小，但是对于开方运算来说还是比较大的。因此我们不打算尝试小加密指数爆破。

因此我们似乎只能分析其他攻击路径。那么我开始尝试有限域开根(可以思考一下，为什么后续攻击也可以不在考虑范围内，这样更真实的还原了做题的情形)。

所以我们先分析是否满足我们的使用条件。如果直接满足就是脚本题了。否则就需要一些处理操作。

e = 0x1337
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
n = p * qprint((p - 1)*(q - 1) % e) # 0
print((p - 1) % e)         # 0
print((q - 1) % e)         # 0

通过测试程序，我们可以确定可以使用有限域开根。因此有以下脚本。

from gmpy2 import *
from Crypto.Util.number import *
import random
import mathdef onemod(e, q):p = random.randint(1, q-1)while(powmod(p, (q-1)//e, q) == 1):  # (r,s)=1p = random.randint(1, q)return pdef AMM_rth(o, r, q):  # r|(q-1assert((q-1) % r == 0)p = onemod(r, q)t = 0s = q-1while(s % r == 0):s = s//rt += 1k = 1while((s*k+1) % r != 0):k += 1alp = (s*k+1)//ra = powmod(p, r**(t-1)*s, q)b = powmod(o, r*a-1, q)c = powmod(p, s, q)h = 1for i in range(1, t-1):d = powmod(int(b), r**(t-1-i), q)if d == 1:j = 0else:j = (-math.log(d, a)) % rb = (b*(c**(r*j))) % qh = (h*c**j) % qc = (c*r) % qresult = (powmod(o, alp, q)*h)return resultdef ALL_Solution(m, q, rt, cq, e):mp = []for pr in rt:r = (pr*m) % q# assert(pow(r, e, q) == cq)mp.append(r)return mpdef calc(mp, mq, e, p, q):i = 1j = 1t1 = invert(q, p)t2 = invert(p, q)for mp1 in mp:for mq1 in mq:j += 1if j % 1000000 == 0:print(j)ans = (mp1*t1*q+mq1*t2*p) % (p*q)if check(ans):returnreturndef check(m):try:a = long_to_bytes(m).decode('utf-8')if 'NCTF' in a:print(a)return Trueelse:return Falseexcept:return Falsedef ALL_ROOT2(r, q):  # use function set() and .add() ensure that the generated elements are not repeatedli = set()while(len(li) < r):p = powmod(random.randint(1, q-1), (q-1)//r, q)li.add(p)return liif __name__ == '__main__':c = 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741e = 0x1337cp = c % pcq = c % qmp = AMM_rth(cp, e, p)mq = AMM_rth(cq, e, q)rt1 = ALL_ROOT2(e, p)rt2 = ALL_ROOT2(e, q)amp = ALL_Solution(mp, p, rt1, cp, e)amq = ALL_Solution(mq, q, rt2, cq, e)calc(amp, amq, e, p, q)

三、基于小加密指数的CRT

基于小加密指数的CRT，基本有以下特征。e的大小就是方程组的数目。

[0CTF 2016] rsa

思路：

下载附件，我们可以获取得到两个文件。其中pem可以使用openssl指令获取里面的内容。当然也可以使用其他方式例如：

from Crypto.PublicKey import RSA
f = open("public.pem")
data = f.read()
s = RSA.importKey(data)
print(s.n)
print(s.e)n = 23292710978670380403641273270002884747060006568046290011918413375473934024039715180540887338067
e = 3
f.close()f = open("D:/Desktop/enter/flag.enc", 'rb')
data = f.read()
print(bytes_to_long(data))
c = 2485360255306619684345131431867350432205477625621366642887752720125176463993839766742234027524

读取完文件后，我们已知的消息有(n, e, c), 其中我们需要求解m，那么我需要知道因子才能获取得到d，进而获取得到m。

print(n.bit_length())

#314

看到n的位数很小，因此我们可以分解n。

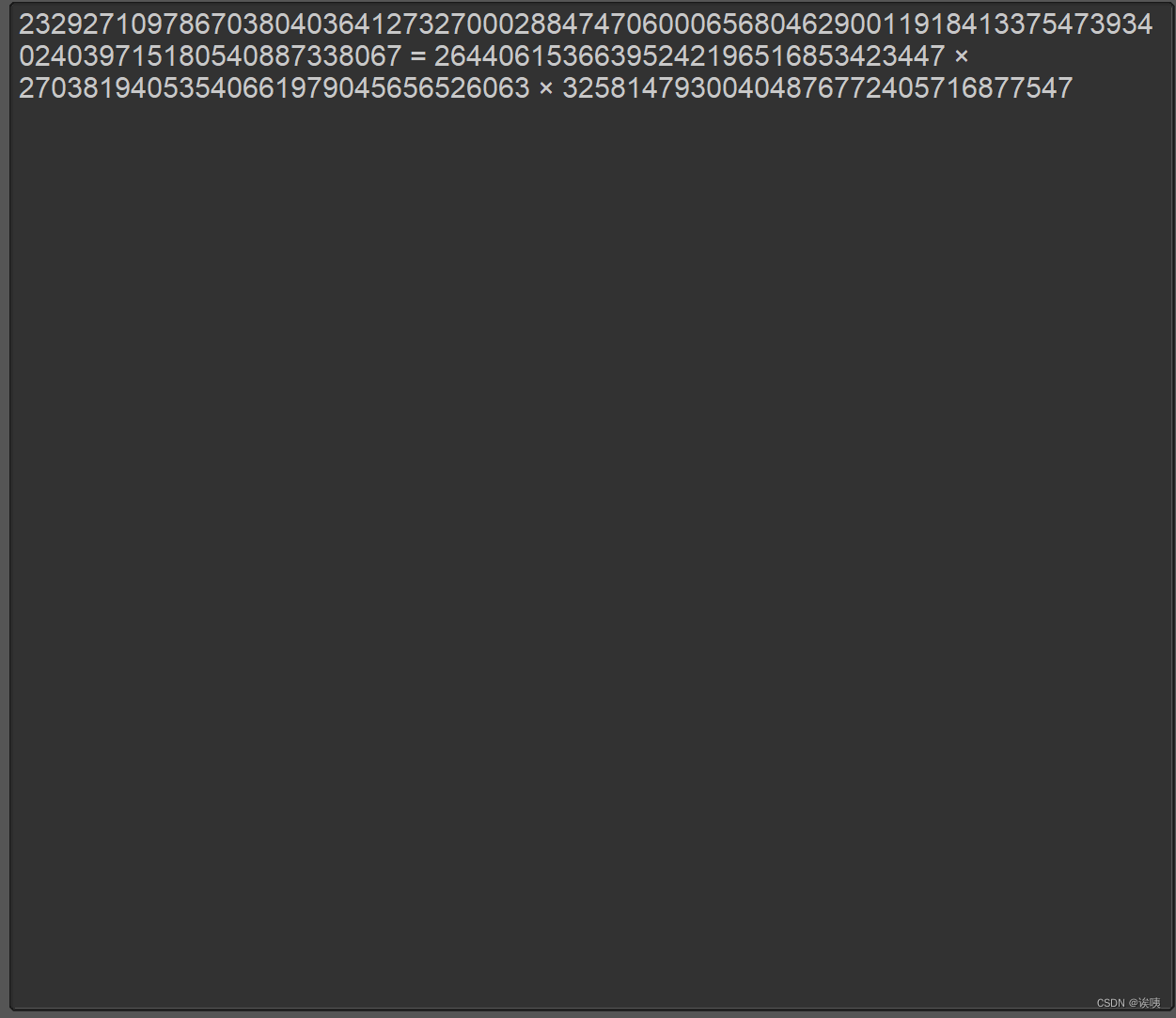
p = 26440615366395242196516853423447

q = 27038194053540661979045656526063

r = 32581479300404876772405716877547

接下来分析数据特征

print((p - 1) * (q - 1) * (r - 1) % e)

print((p - 1) % e)

print((q - 1) % e)

print((r - 1) % e)

在关注到e的大小为因子的数目，从模数运算角度出发，拆分是一种极其重要的思维。所以我们可以通过拆分n得到足够的方程数。所以，我们需要将CRT纳入考虑范围。除此之外，我们还应该考虑到，有且仅有(q - 1)不是e的倍数，因此还要考虑有限域开根或者说是解方程。获取得到c的e根次。

p = 26440615366395242196516853423447
q = 27038194053540661979045656526063
r = 32581479300404876772405716877547
ct = 2485360255306619684345131431867350432205477625621366642887752720125176463993839766742234027524PR.<x> = PolynomialRing(Zmod(p))
f = x^3-ct
res1 = f.roots()
PR.<x> = PolynomialRing(Zmod(q))
f = x^3-ct
res2 = f.roots()
PR.<x> = PolynomialRing(Zmod(r))
f = x^3-ct
res3 = f.roots()for x in res1:for y in res2:for z in res3:m = crt([int(x[0]),int(y[0]),int(z[0])],[int(p),int(q),int(r)])if b'0ctf'in long_to_bytes(m):print(long_to_bytes(m))