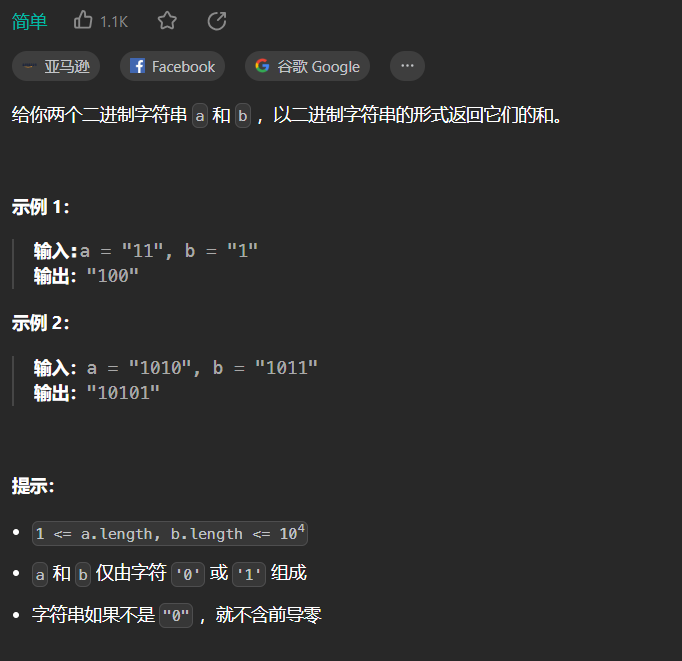
67.二进制求和

方法：模拟计算

class Solution {public String addBinary(String a, String b) {StringBuilder ans = new StringBuilder();int carry = 0;for(int i=a.length()-1,j=b.length()-1;i>=0||j>=0;i--,j--){int sum = carry;sum += i >=0 ? a.charAt(i) - '0': 0;sum += j >= 0 ? b.charAt(j) - '0': 0;ans.append(sum % 2);carry = sum / 2;}ans.append(carry == 1 ? carry : "");return ans.reverse().toString();}
}