第4章 随机变量的数字特征
4.1数学期望
一、离散型随机变量的数学期望
定义1设离散型随机变量X的概率分布为 P{X=xi}=pi,i=1,2,…,如果级数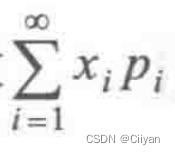 绝对收敛,则定义X的数学期望(又称均值)为
绝对收敛,则定义X的数学期望(又称均值)为
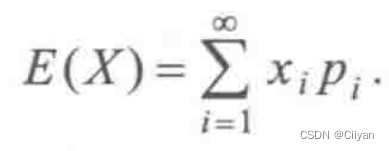
二、连续型随机变量的数学期望
定义2设X是连续型随机变量,其密度函数为f(x).如果f-∞+∞xf(x)dx 绝对收敛,则定义X的数学期望为
E(X)=f-∞+∞xf(x)dx
三、随机变量函数的数学期望
- 定理1:设X是一个随机变量,Y=g(X),且E(Y)存在,于是
(1)若X为离散型随机变量,其概率分布为
P{X=xi}=pi,i=1,2,…,
则Y的数学期望为
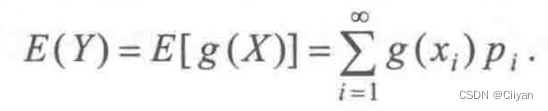
(2)若X为连续型随机变量,其概率密度为f(x),则Y的数学期望为
E(Y)=E[g(X)]=f-∞+∞g(x)f(x)dx. (1.4) - 定理2:设(X,Y)是二维随机变量,Z=g(X,Y),且E(Z)存在,于是
(1)若(X,Y)为离散型随机变量,其概率分布为
P{X=xi,Y=yi}=pij(i,j=1,2,…),
则Z的数学期望为
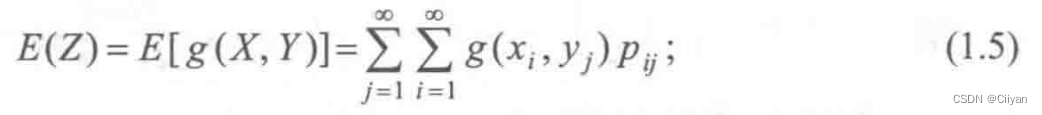
(2)若(X,Y)为连续型随机变量,其概率密度为f(x,y),则Z的数学期望为
E(Z)=E[g(X,Y)]=f-∞+∞f-∞+∞g(x,y)f(x,y)dxdy. (1.6)
四、数学期望的性质
性质1若C是常数,则E( C)=C.
性质2若C是常数,则E(CX)=CE(X),
性质3E(X1+X2)=E(X1)+E(X2)

性质4设X,Y相互独立,则E(XY)=E(X)E(Y):
X和Y相互独立,f(x,y)=fX(x)·fY(y),
**
4.2方差
一、方差的定义
- 定义1设X是一个随机变量,若E[X-E(X)]2存在,则称它为X的方差,记为
D(X)=E[X-E(X)]2.
注:符号D(X)有时简写为DX.同样,对于连续型随机变量也是这样规定 - 方差的算术平方根√D(X)称为标准差或均方差.它与X具有相同的度量单位.
注:方差刻画了随机变量X的取值与数学期望的偏离程度,它的大小可以衡量随机变量取值的稳定性 - 从方差的定义易见:
(1)若X的取值比较集中,则方差较小;
(2)若X的取值比较分散,则方差较大;
(3)若方差D(X)=0,则随机变量X以概率1取常数值,此时,X也就不是随机变量了.
二、方差的计算
若X是离散型随机变量,且其概率分布为
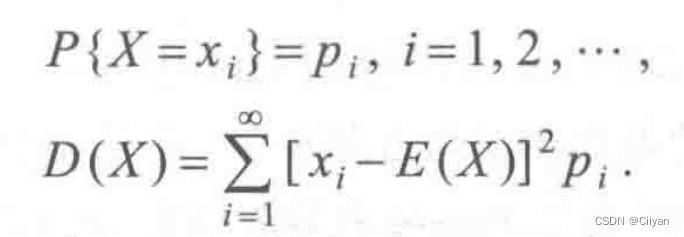
若X是连续型随机变量,且其概率密度为∫(x),则
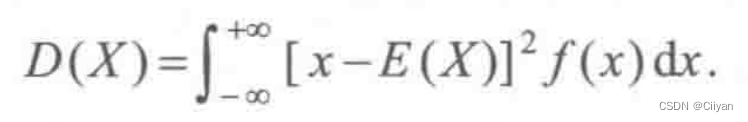
由数学期望的性质,易得计算方差的一个简化公式:
**D(X)=E(X2)-[E(X)]2
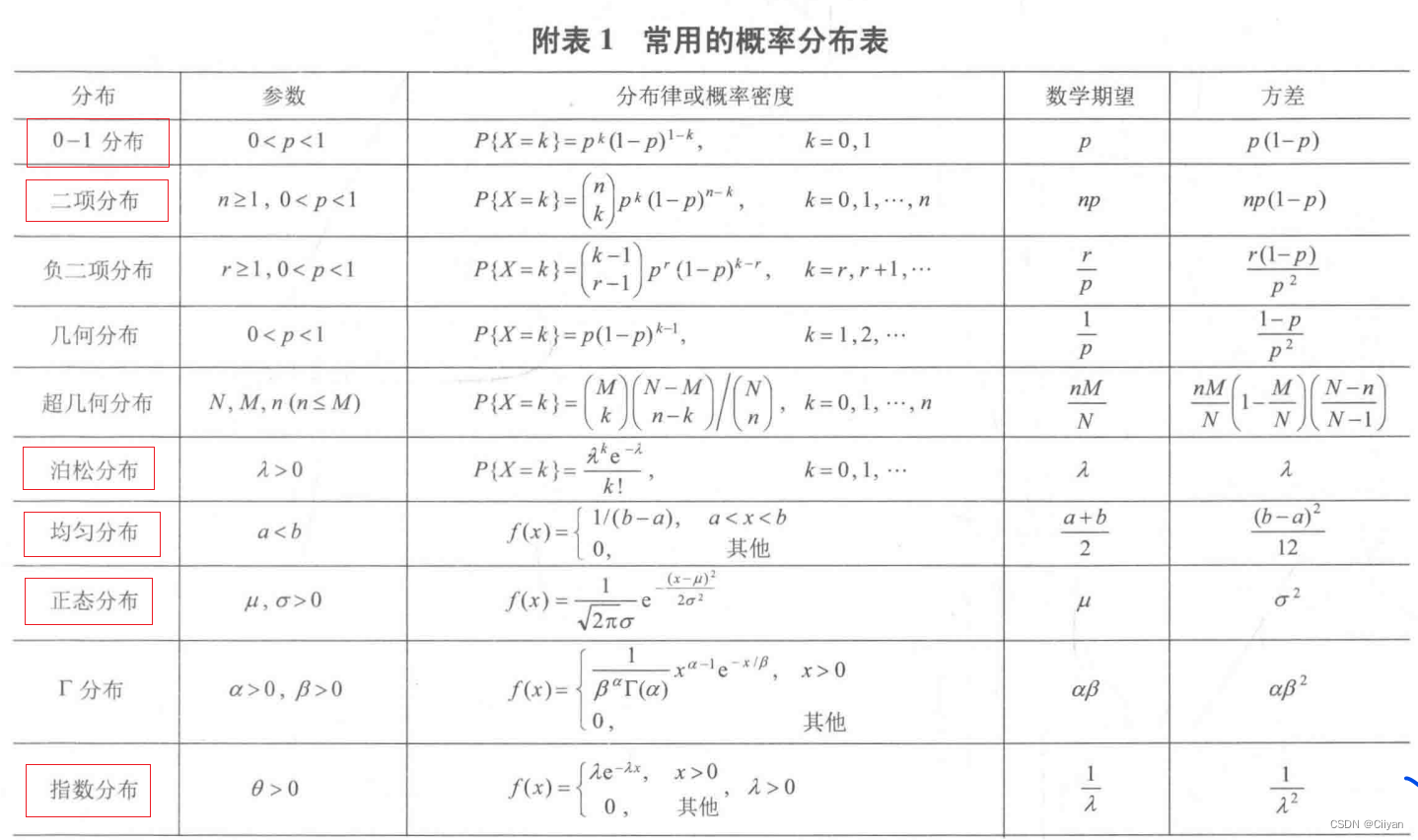
- 0-1分布
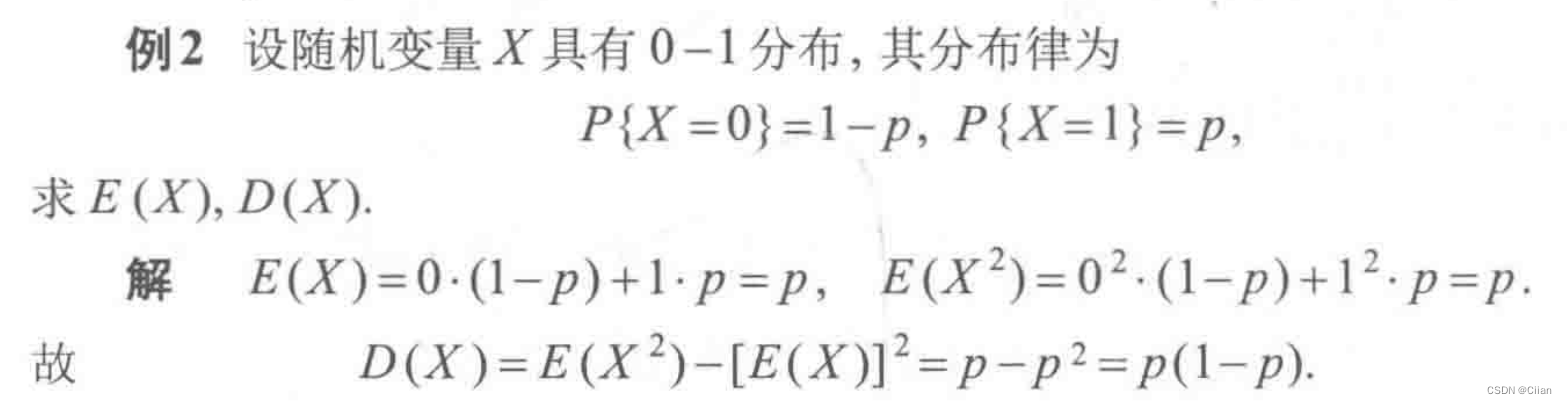
- 泊松分布
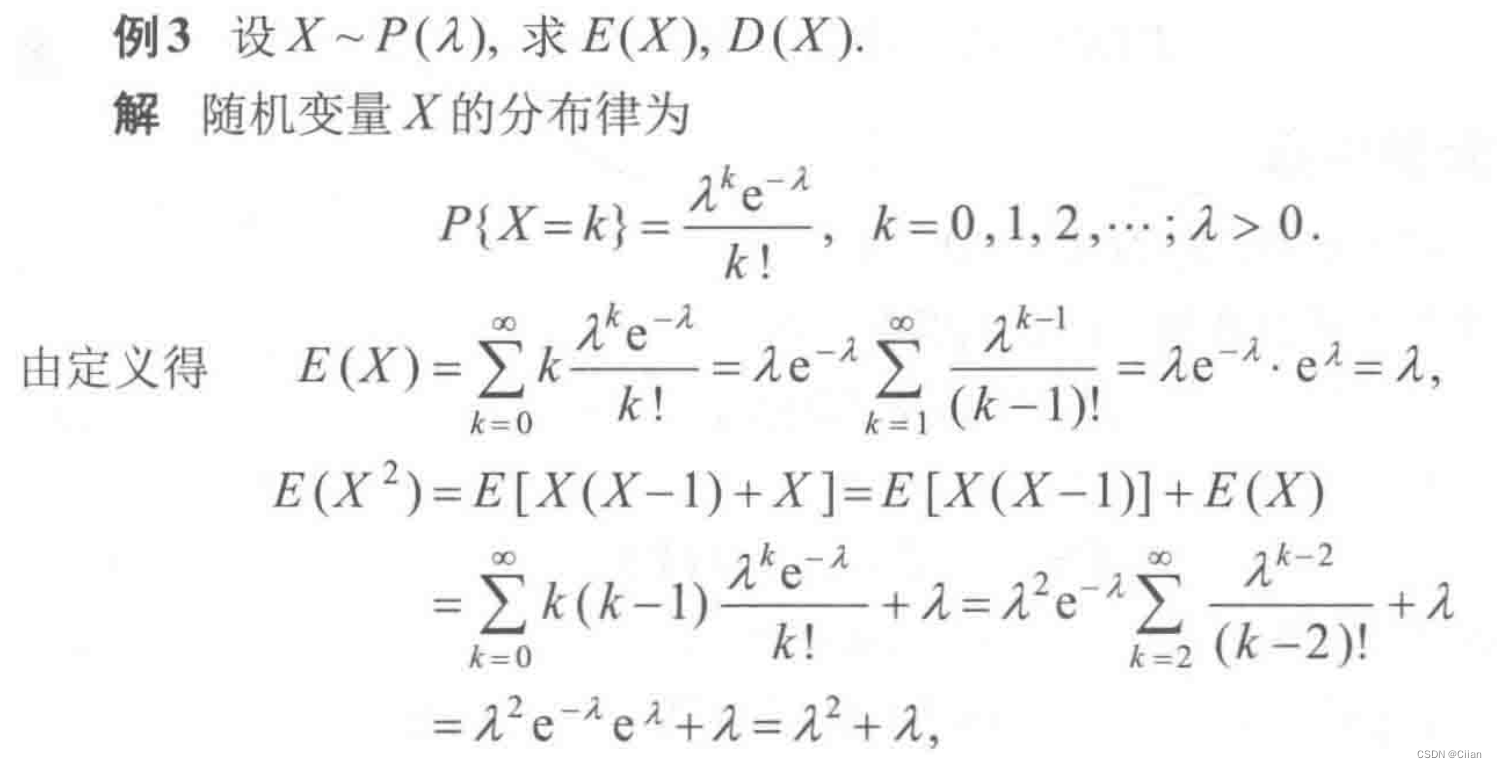
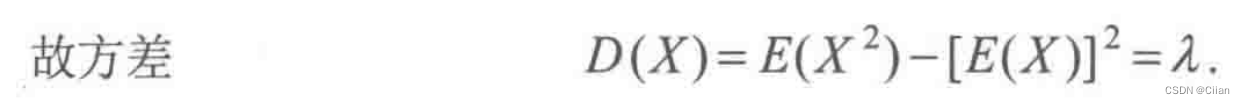
- 均匀分布
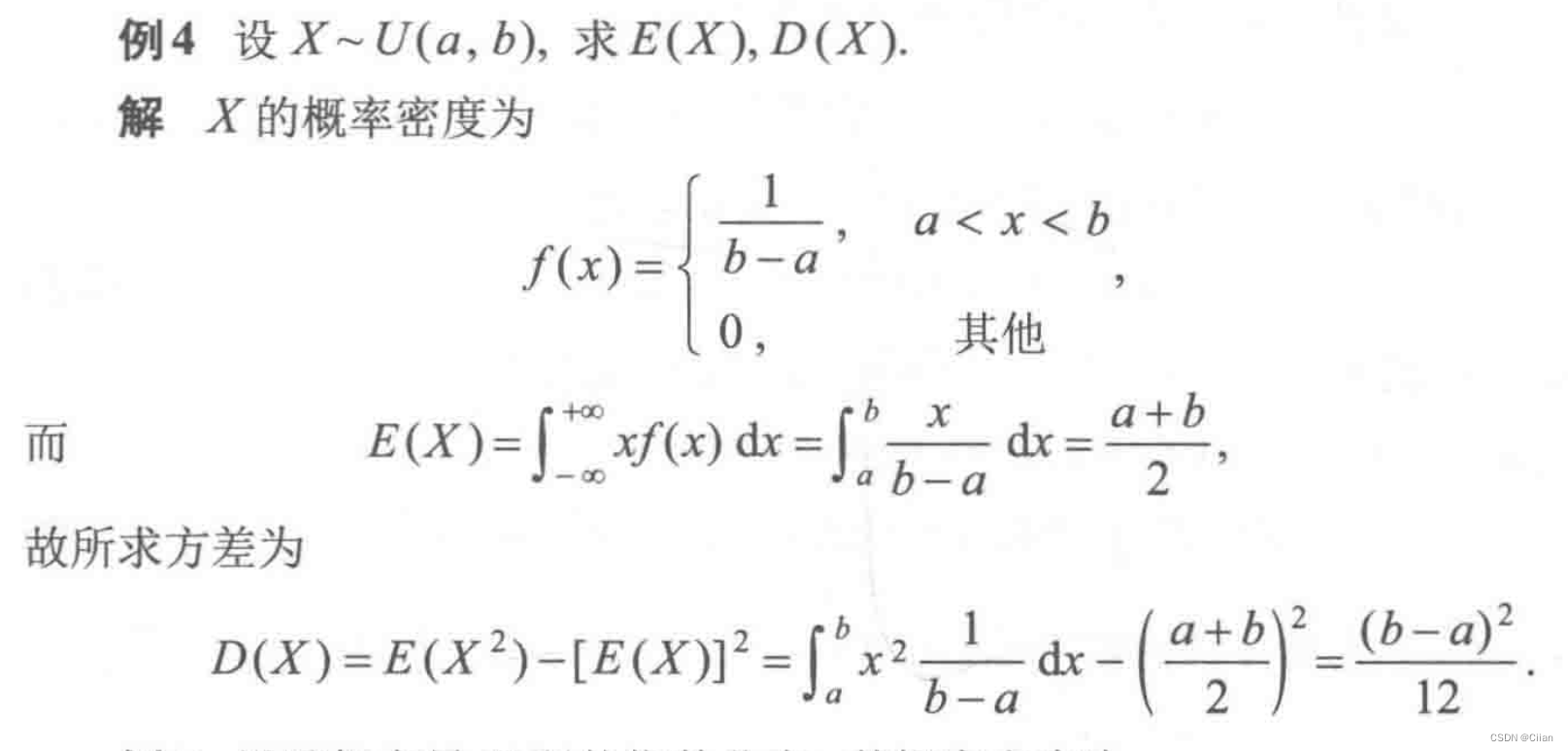
- 二项分布

- 正态分布

- 标准正态分布
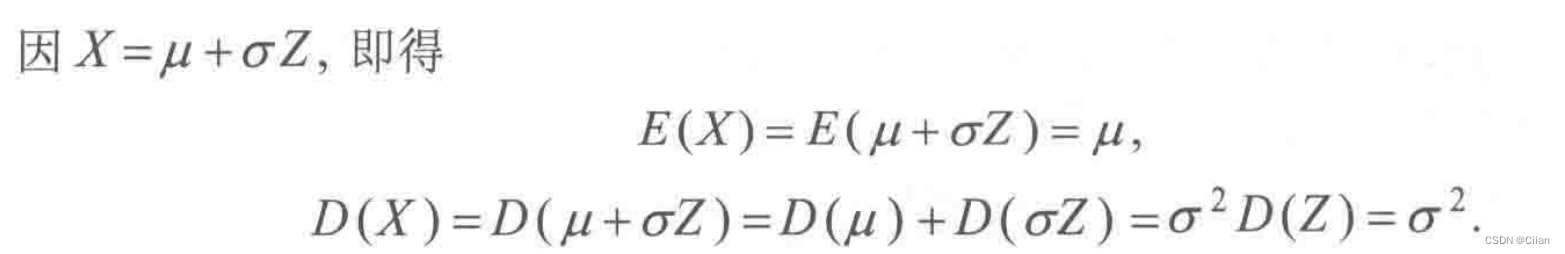
三、方差的性质
性质1:设C为常数,则D©=0.
D(X+C)=D(X)
性质2:设X是随机变量,若C为常数,则
D(CX)=C2 D(X)
性质3:若X,Y相互独立,则
D(X±Y)=D(X)+D(Y)
4.3 协方差与相关系数
*八、n维正态分布的几个重要性质
(2)n维随机变量(Xi,X2,…,Xn)服从n维正态分布的充分必要条件是X1,X2,…,Xn的任意线性组合C1X1+C2X2+…+CnXn均服从一维正态分布(其中C1,C2,…,Cm不全为零)
(3)若(X1,X2,…,Xn)服从n维正态分布,设Y1,Y2,…,Yk是Xj(j=1,2,…,n)的线性函数,则(Y1,Y2,…,Yk)服从k维正态分布.
4.4大数定律与中心极限定理
一般的大数定律讨论个随机变量的平均值的稳定性
一、切比雪夫(Chebyshev)不等式
定理1设随机变量X的期望E(X)=μ,方差D(X)=σ2,则对于任意给定的正数ε,有
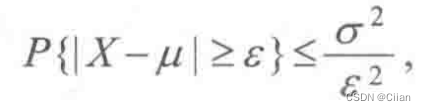
这个不等式称为切比雪夫不等式
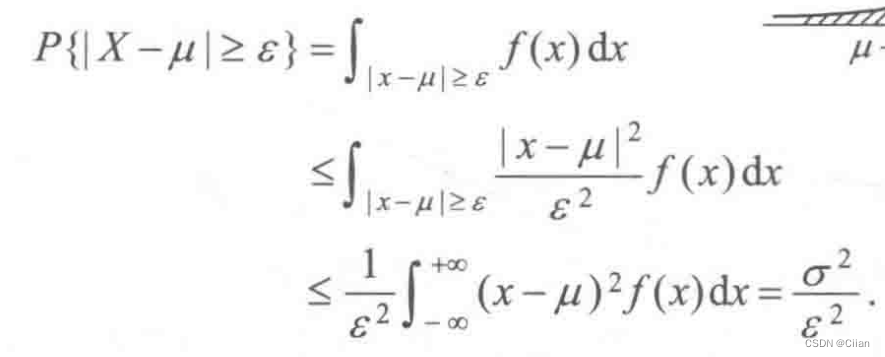
切比雪夫不等式也可以写成
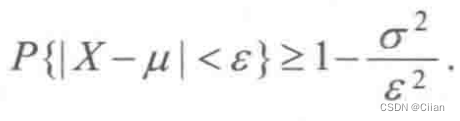
切比雪夫不等式表明:随机变量X的方差越小,则事件{|X-μ|<ε}发生的概率越大,即X的取值基本上集中在它的期望μ附近
- 在方差已知的情况下,切比雪夫不等式给出了X与它的期望u的偏差不小于的概率的估计式,如取ε=3σ,则有
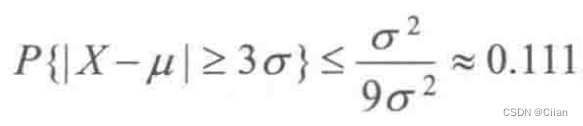
于是,对任意给定的分布,只要期望和方差存在,则随机变量X取值偏离μ超过3倍均方差的概率小于0.111.
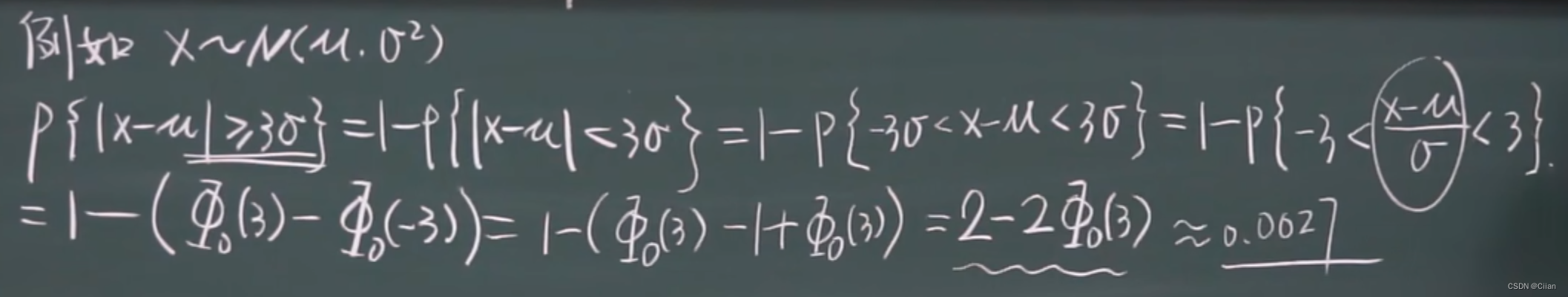
二、大数定律
定理2设随机变量X,X2,…,Xn,…相互独立,且具有相同的期望和方差:
E(X)=μ,D(X)=σ2,i=1,2,….
记频率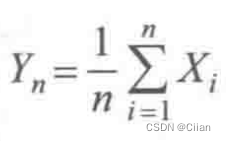 ,则对任意ε>0,有
,则对任意ε>0,有
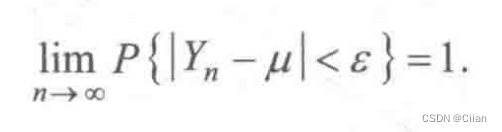
证明
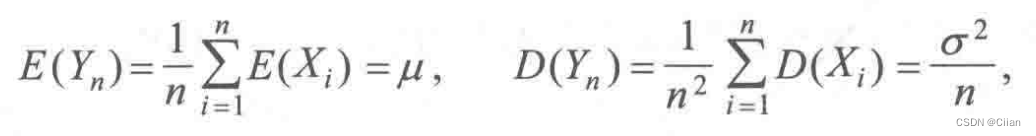
由切比雪夫不等式,得
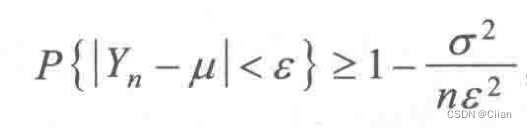
令n→oo,再注意到概率不可能大于1,由夹逼定理可得结论。
三、中心极限定理
在实际问题中,许多随机现象是由大量相互独立的随机因素综合影响形成的,其中每一个因素在总的影响中所起的作用是微小的.这类随机变量一般都服从或近似服从正态分布.
-
定理3:(独立同分布的中心极限定理):设随机变量X1,X2,…,Xn,…相互独立,服从同一分布,且E(Xi)=μ,D(Xi)=σ2(i=1,2,…),则
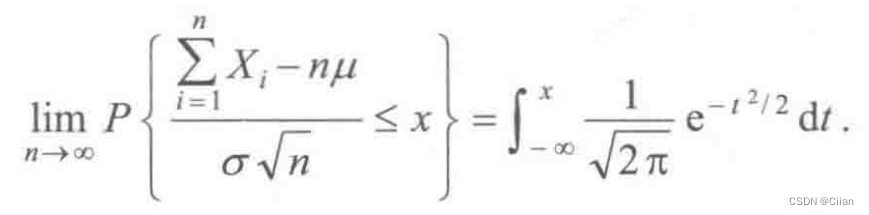
左边的分布函数近似右边标准正态分布 -
正态分布,
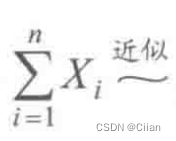 N(μ,nσ2), 其标准正态分布
N(μ,nσ2), 其标准正态分布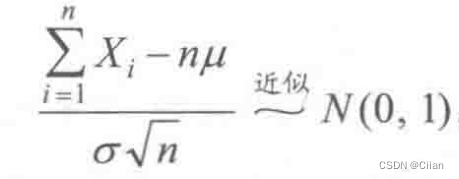
-
正态分布,
 , 其标准正态分布
, 其标准正态分布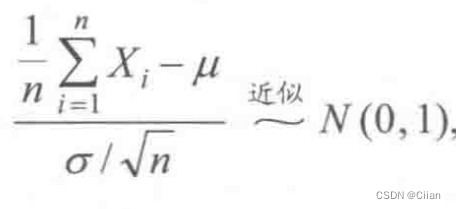
-
例2一盒同型号螺丝钉共有100个,已知该型号的螺丝钉的重量是一个随机变量,期望值是100g,标准差是10g,求一盒螺丝钉的重量超过10.2kg的概率.
解:设Xi,为第i个螺丝钉的重量,i=1,2,…,100,且它们之间独立同分布,于是,一盒螺丝钉的重量为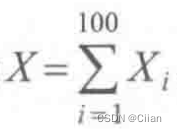 ,而且
,而且
μ=E(Xi)=100,σ=√D(Xi)=10,n=100.
由中心极限定理有
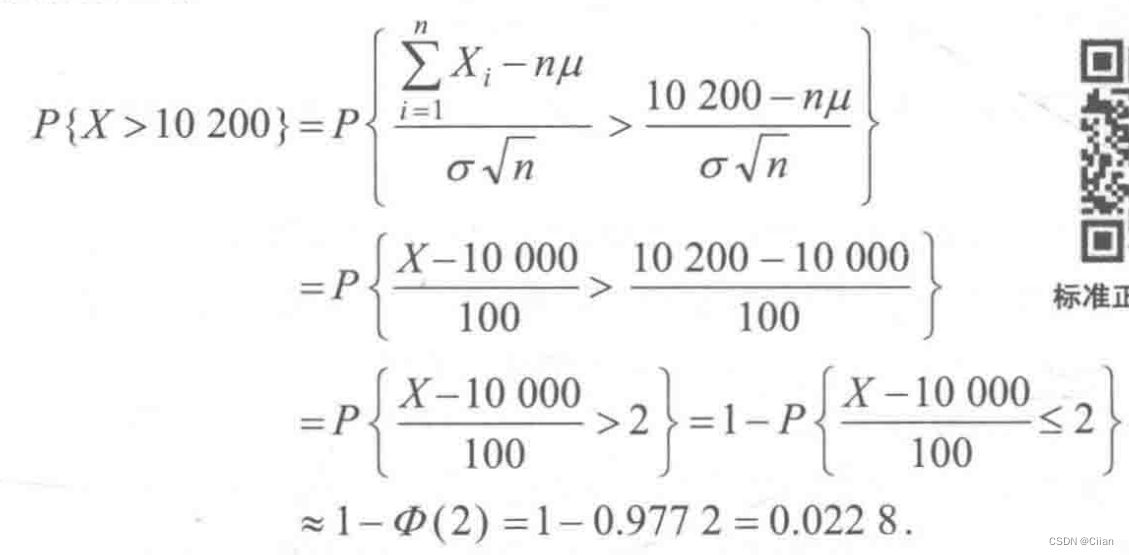
即一盒螺丝钉的重量超过10.2kg的概率为0.0228. -
例5某市保险公司开办一年人身保险业务,被保险人每年需交付保险费160元,若一年内发生重大人身事故,其本人或家属可获2万元赔偿金.己知该市人员一年内发生重大人身事故的概率为0.005,现有5000人参加此项保险,问保险公司一年内从此项业务中所得到的总收益在20万元到40万元之间的概率是多少?
解记
于是,X:均服从参数为p=0.005的两点分布,P{Xi=1}=0.005,np=25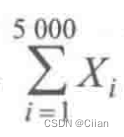 是5000个被保险人中一年内发生重大人身事故的人数,保险公司一年内从此项业务中所得到的总收益为
是5000个被保险人中一年内发生重大人身事故的人数,保险公司一年内从此项业务中所得到的总收益为
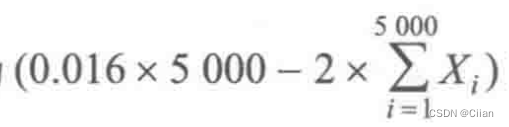 万元.所以
万元.所以
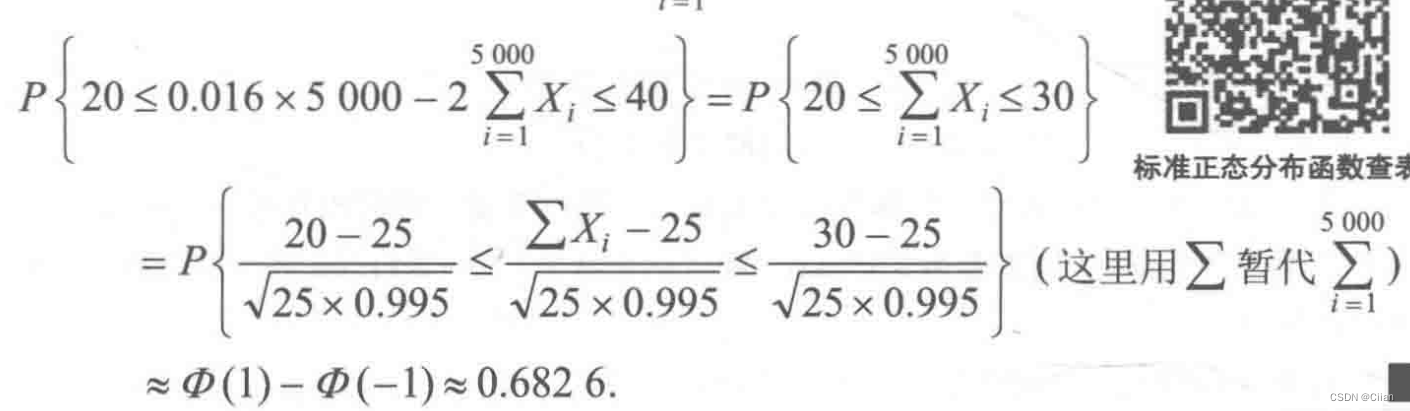





![[Spring ~必知必会] Bean 基础常识汇总](https://img-blog.csdnimg.cn/img_convert/549241c9d7c3f383312e88ca73a16f9d.png)