IEEE WCCI-2020电动汽车路由问题进化计算竞赛的基准集-编程知识

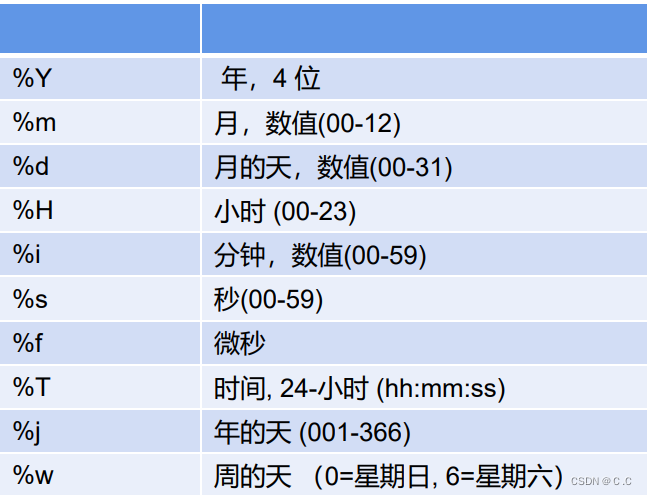
引言

交通一直是二氧化碳排放的主要贡献者。由于全球变暖、污染和气候变化，联邦快递、UPS、DHL和TNT等物流公司对环境变得更加敏感，他们正在投资于减少作为其日常运作的一部分而产生的二氧化碳排放的方法。毫无疑问，使用电动汽车（EVs）而不是传统汽车将大大有助于减少二氧化碳的排放[1]，这一事实增加了物流公司利用电动汽车进行日常运营的兴趣。在这种情况下，出现了一个电动车队的路由问题，即电动汽车路由问题（EVRP）[2]。在本报告中，提供了一个EVRP实例的基准集，其中有已知和未知的最佳值。本报告的其余部分组织如下。第2节介绍了EVRP问题，其中提出了该问题的详细数学表述。第3节给出了EVRP基准集的细节。第4节展示了在基准集上评估算法的标准。最后第5节总结了本报告。

2 电动汽车路由问题

EVRP是一个具有挑战性的NP-hard组合优化问题，因为它是普通短路径问题的扩展，包含了额外的约束条件[3]。EVRP可以描述如下：给定一个电动车队，我们需要为每个电动车在其电池充电水平限制内找到可能的最佳路线，开始和结束于中央仓库，为一组客户服务。通常，这个问题用全连接加权图G = (V,A)来表示，其中V = {0∪I ∪F ′ }是一组节点，A = {(i,j) | i,j ∈V,i 6 = j }是一组连接这些节点的弧。集合I表示客户的集合，集合F′表示每个充电站i∈F的β i节点副本1的集合（即|F′|=∑i∈Fβ i），0表示中心仓库。每条弧都有一个非负值距离d ij，代表节点i和j之间的欧几里得距离。每条行进的弧（i,j）消耗穿越该弧的电动车剩余电池电量hd ij，其中参数h表示电动车的消耗率。此外，每个客户i∈I被分配一个正的需求b i2。

假设有一个同质的电动车队，EVRP的目标函数是找到一组路线，使行驶的总距离最小。

每个客户正好被一辆电动车访问一次

--所有的电动车都从仓库开始（满载并充电）并在仓库结束

--对于每条电动车路线，客户的总需求不超过电动车的最大承载能力C

--对于每条电动车路线，总能耗不超过电动车的最大电池充电水平Q

--电动车总是离开充电站完全充电（注意，仓库也被认为是一个充电站）

--充电站（包括仓库）可以被任何电动车多次访问

因此，EVRP可以在数学上表述如下：

其中公式。(1)定义了EVRP的目标函数，公式。(2) 强制执行客户访问的连通性，公式。(3)处理充电站的连接问题，公式。(4) 通过保证每个节点，即传入弧的数量等于传出弧的数量来建立流量保护。公式。(5)和公式。(6) 通过在到达包括仓库在内的任何节点时保证非负的承载负荷，保证所有客户的需求得到满足，公式。(7), 公式(8)和公式(7)。(9)确保电池电荷永远不会低于0，而公式。(11)定义了一组二元决策变量，如果有弧线行驶，每个变量等于1，否则等于0。变量u i和y i分别表示电动车到达节点i∈V时的剩余承载能力和剩余电池电量。

3 EVRP基准集的描述

EVRP基准集由两组问题组成：

1.由7个小问题实例（最多100个客户）组成，其中提供了它们的最佳上界值。

2. 由10个较大的问题实例组成（最多1000个客户），其中没有提供其上限值。

第一组EVRP实例是通过扩展Christofides和Eilon[6]的传统车辆路由问题的著名实例产生的（见图1），

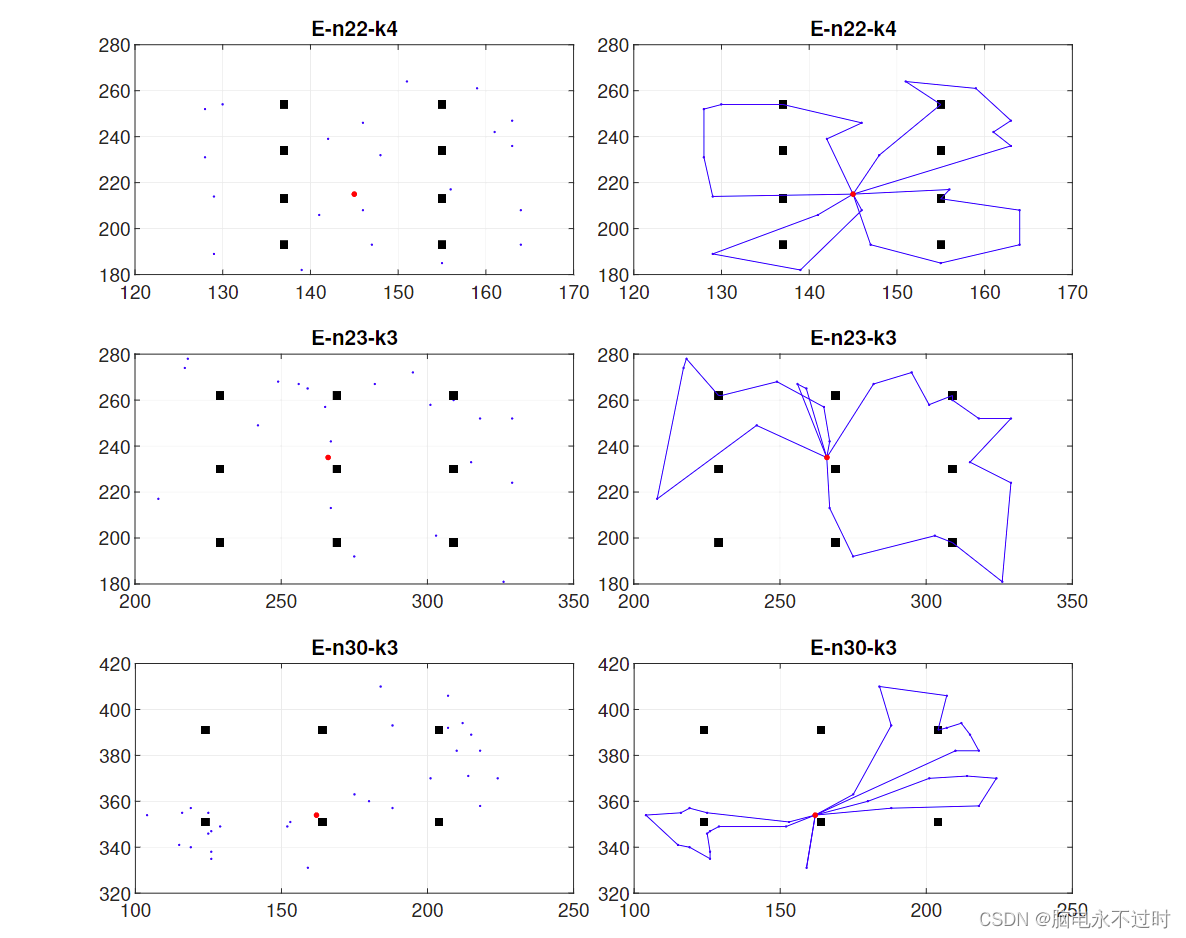
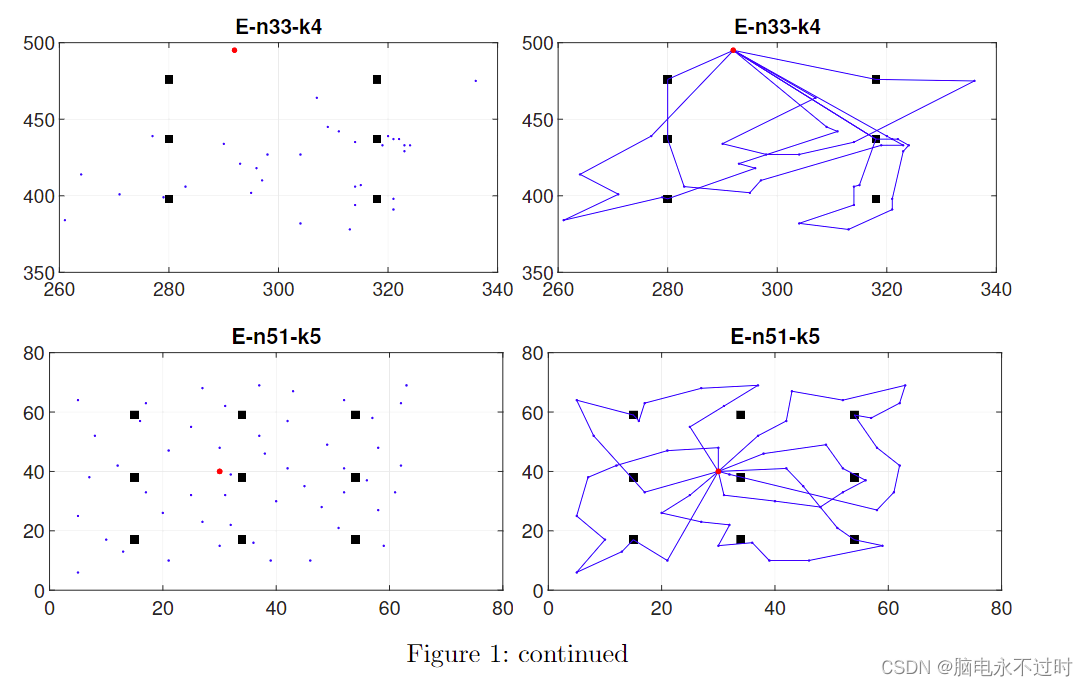
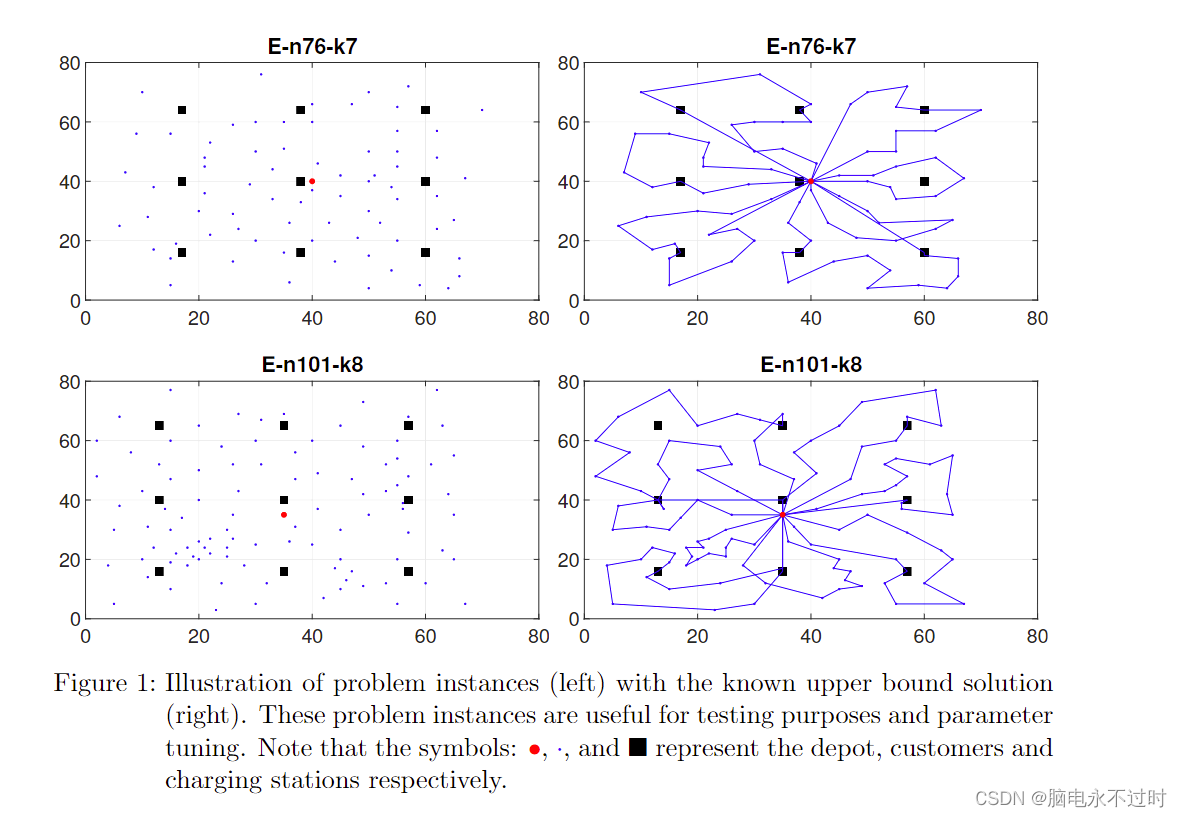
图1：问题实例（左）与已知上界解（右）的说明。这些问题实例对于测试目的和参数调整很有用。请注意，大圆点，小圆点，方块分别代表仓库、客户和充电站。

而第二组是Uchoa等人[7]最近的传统车辆路由问题的实例的扩展。（见图2）。

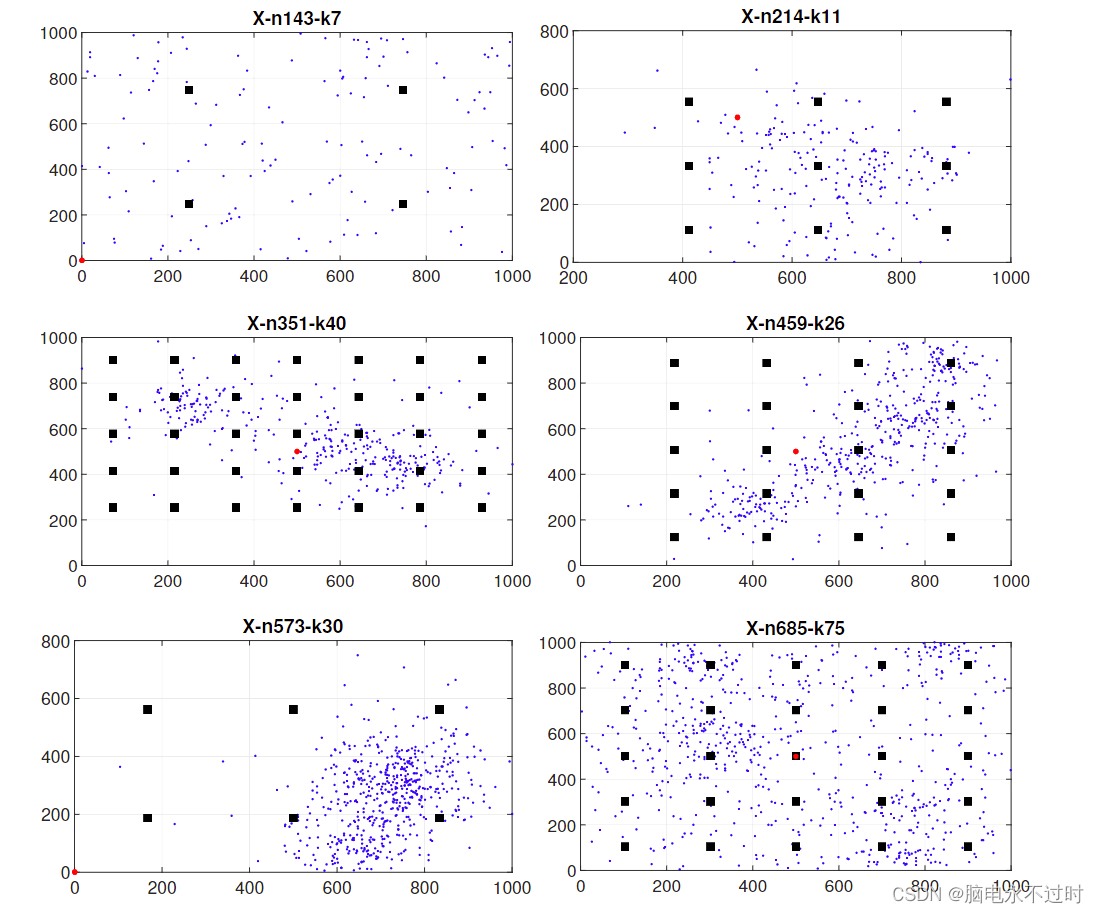
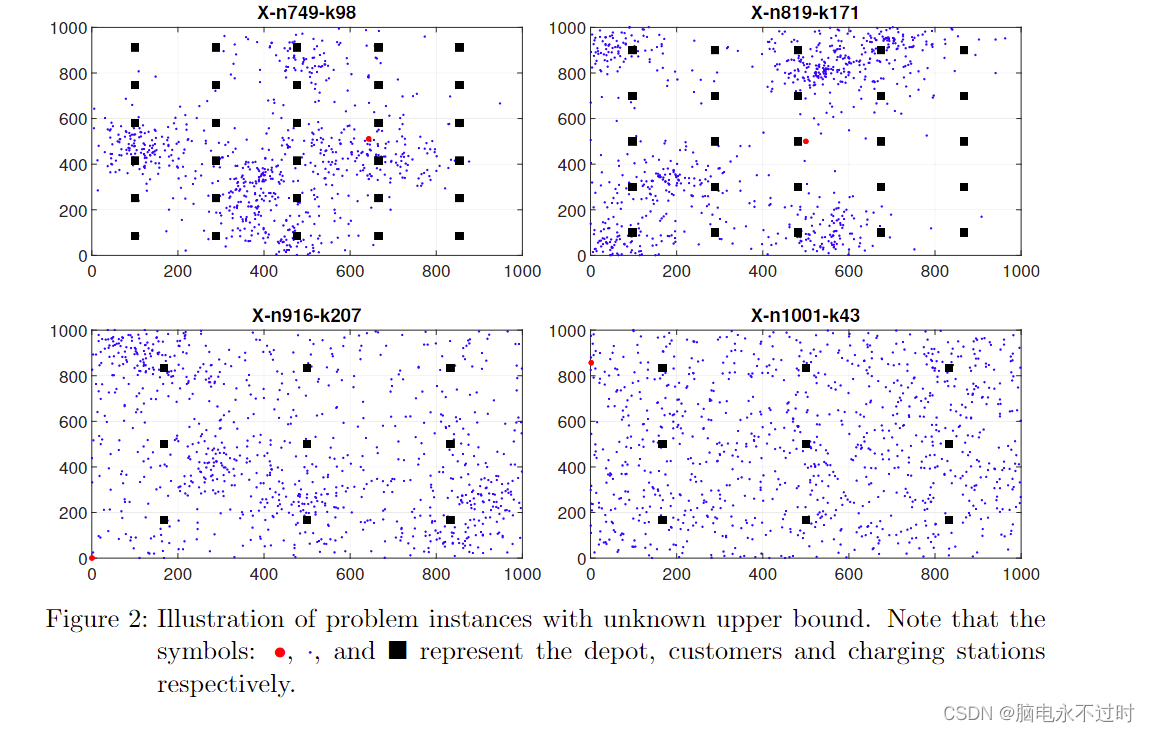
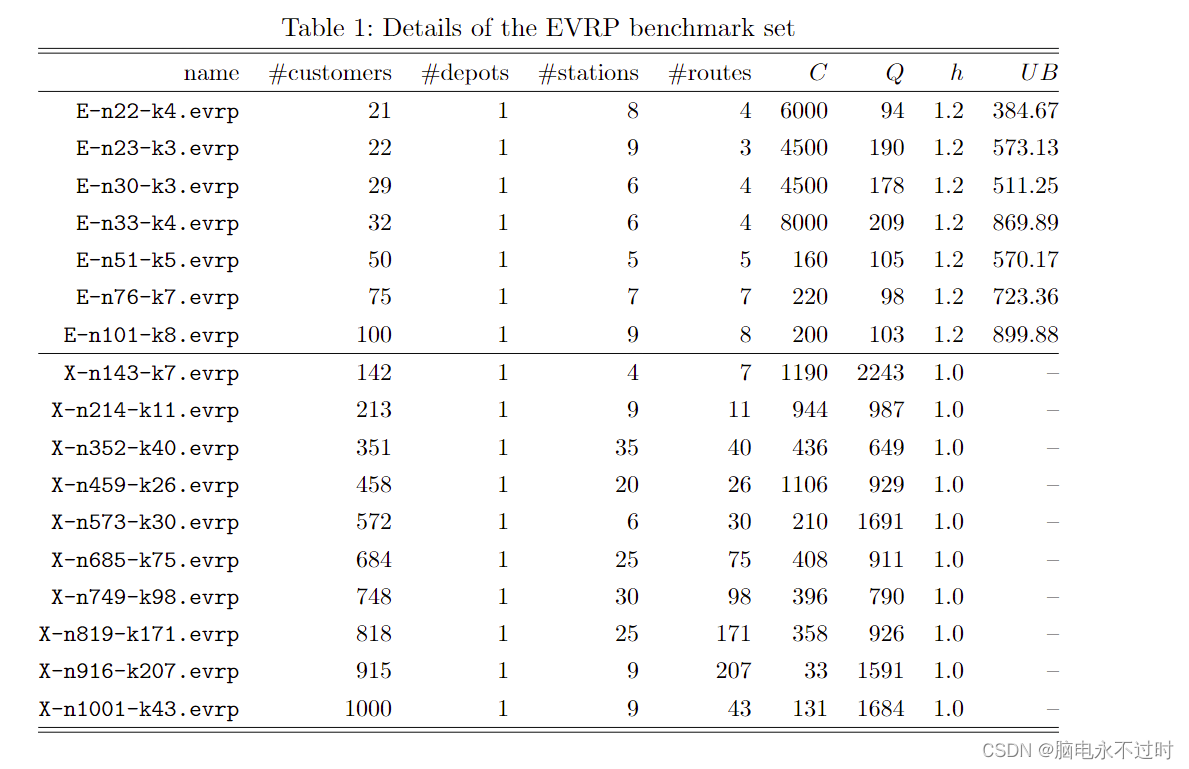
第一组的实例对测试很有用（例如，求解器的验证、参数调整等），因为大问题实例的解决更具挑战性和耗时。表1中总结了所有生成的EVRP实例的细节。表1中的各栏列出了客户数量、仓库数量、充电站数量、最小路线数量、电动车的最大负荷（C）、电动车的最大电池充电水平（Q）、能耗常数（h）和最佳上限（UB）值（在某些情况下可能是最佳值，但尚未得到验证）。

DIMENSION：包括中央仓库在内的客户数量

- STATIONS：充电站数量

- CAPACITY电车容量：电动车的最大承载能力（即C）

- ENERGY CAPACACITY电量上限：电动车的最大电池充电水平（即Q）

- ENERGY CONSUMPTION能量消耗：恒定的电荷消耗率（即h）

•EDGE WEIGHT FORMAT 边的距离：欧氏距离

•NODE COORD SECTION 节点部分：该部分包含节点的信息，格式为节点id、x和y坐标

•DEMAND SECTION需求部分：该节包含每个客户的需求，以节点id和需求的格式（即，b i）

•STATIONS COORD SECTION :站点合作部分：本部分包含充电站的节点id

•DEPOT SECTION车辆段部分：本节包含中央车辆段的节点id。

在竞赛网站4中，文件（EVRP.hpp）中提供了一个能够读取所有上述信息的源代码样本（即读取扩展名为.evrp的文件），可以通过相应的函数来利用。更具体地说，EVRP.hpp中实现的功能可以用来生成EVRP实例的距离矩阵，访问所有上述信息，并评估由求解器生成的解决方案（注意，解决方案必须是源代码中描述的特定格式）。此外，文件stats.hpp的实现提供了可以用来保存解算器结果的函数，可以提交给比赛。我们强烈鼓励参与者利用所提供的文件main.cpp，并在heuristic.cpp文件中实现他们的方法。最后，表1中描述的基准集也可以在完成网站上找到。

评价标准

- 问题实例。表1总结了17个EVRP实例

- 独立运行。如果实现的启发式是随机的，那么运行20次独立的运行（用1−20的随机种子）；否则运行一次。在样本代码中已经定义为MAX TRIALS .

- 评价。最大的评价次数是25000n，其中n = |I | + 1 +|F |是问题实例的大小。一次评估的复杂度为O(n2)。

- 终止条件。当算法达到上面定义的最大评估次数时[换句话说，调用公式中的目标函数。(1)]。在样本代码中已经定义为TERMINATION。

- 测量。从所有评价中找到的最佳解决方案在多次独立运行中的平均值如下：

其中R是独立运行的数量（即随机方法的R = 20，确定性方法的R = 1），P ∗ i是运行i中所有评估中找到的最佳解决方案。

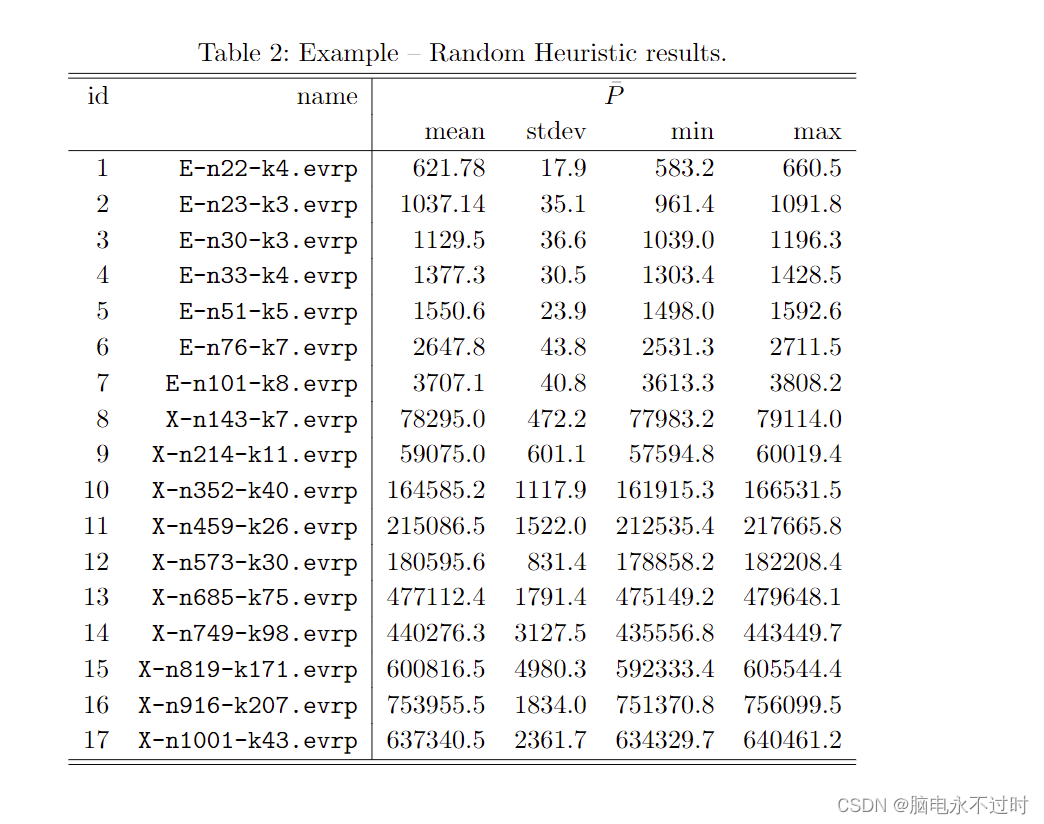
注意：P-的测量已经在样本代码中实现（在stats.hpp中），并存储在代码执行时产生的输出文本文件中。参与者可以简单地提交这些为每个实例获得的输出文本文件，以及他们算法的细节和源代码。表2显示了从源代码（文件heuristic.hpp）中实现的样本启发式得到的结果的例子，其中 "mean "是20次运行的平均解决方案质量，stdev "是标准偏差，min "是20次运行的最佳结果，max "是20次运行中最差的结果。所有这些数值都是在所提供的源代码生成的输出文本文件中计算的。