题干：

现有 r 个互不相同的盒子和 n 个互不相同的球，要将这 n 个球放入 r 个盒子中，且不允许有空盒子。请求出有多少种不同的放法。

两种放法不同当且仅当存在一个球使得该球在两种放法中放入了不同的盒子。

数据范围：

0<=n,r<=10

思路很简单：还是补集的思想，假设A为所有不合法的放法，U为所有的放法，

答案就是 U-A

那么所有的放法 怎么求呢？

每一个球可以放的盒子有r种选择，有n个小球，所以总方案数就是：r^n种

那么A怎么求呢？

由于每个盒子都不空的方法是合法操作，那么有盒子空的方法就是不合法操作，

又可以分为，指定某1个盒子必然空其余盒子随意，指定某2个盒子空…………

指定某r-1个盒子是空的，其余盒子随意

（有些人看到这里可能会问，为啥要这样设啊，不能直接1个盒子空，2个盒子空……

这样吗，事实上是因为这样更难算，所以没有这样设，如果你直接算出来了一个盒子空有多少种，俩盒子空有多少种……那直接相减就行了，还用个毛容斥原理

指定某个盒子必然为空，更好算，因为其余的盒子只要随机放就可以了。）

当指定1个盒子是空的 的放法设为A1 ，首先从r个盒子里挑1个为空盒子，有C（r，1）=r种情况，

然后将所有球放入 r-1个盒子中，随意放置  有   （r-1）^n

所以当指定1个盒子是空的放法：C（r，1）*（r-1）^n

当指定k个盒子是空的放法：C（r，k）*  （r-k）^ n

由容斥原理，我们要求所有的方法的并集（因为这些方法直接是有相交的部分的）

总不和法的方法就是：

由于我们需要算合法的方法，所以真正的答案就是：

整合起来：

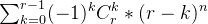
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
#include<iomanip>
using namespace std;
long long pw(int a, int b) {long long s = 1;while (b) {if (b & 1)s = s * a;a = a * a;b >>= 1;}return s;
}
long long C(int r, int k) {if (r < k)return 0;long long s = 1;for (int i = r; i > r - k; i--) {s *= i;s /= (r - i + 1);}return s;
}
int main() {int n, r;cin >> n >> r;long long ans = 0;for (int k = 0; k <= r - 1; k++) {ans += ((k & 1 ? -1 : 1) * C(r, k) * pw(r - k, n));}cout << ans;
}