NumPy

NumPy介绍

在Python中有列表和数组模块，但是都不好用，列表的缺点是要保存每个对象的指针，如果你的列表有一百万个元素，他就有一百万个指针，而数组又只支持一维数组，并不适合数值运算

NumPy的模块支持数组和矩阵(向量)的运算，对机器学习算法比较友好，支持n维数组，有强大的数学运算对很多第三方库(SciPy，Pandas)都提供的底层支持

导入NumPy

首先要确保你的安装了NumPy库

pip install numpy

一般我们会给NumPy起别名为np

NumPy数组

序列生成数组

生成数组最简单的方法就是用array()方法，他可以接收任意类型的数据(列表、元组等)作为数据源

需要注意的是，如果各种数据的数据类型不统一，但是数据类型可以相互转换，就会进行自动转换，浮点数和整数都存在时，就会将整数自动转化成浮点数

每一个数组都可以利用dtype数据(ArrName.dtype)来输出数组中数据的类型，如果没有显示指定(ArrName.astype())，数组就会自动推断数据类型

例如

import numpy as np
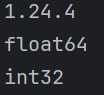
print(np.__version__)list1 = [1, 2, 2.5, 3, 4, 5]arr1 = np.array(list1)
print(arr1.dtype)arr1 = arr1.astype(int)
print(arr1.dtype)

如果数据序列是嵌套的，而且嵌套序列是等长的，就会自动转换为高维数组，例如列表中有两个分别带有4个元素的子列表，数组就会自动变为两行四列的二维数组

函数生成数组

我们可以用arange()方法来生成数组，参数如下

arange(start, stop, step, dtype)

start与stop为起止位置，step为步长，区间为左闭右开，例如

arr3 = np.arange(1, 10, 2, int)
print(arr3)

对于数组的操作有一个是

arr3 = arr3 + 1

需要注意的是这个操作是给所有元素加1，但是这个1实际上是利用了“广播机制”，将1扩展为等长的数组，才能进行相加

range，arange，linspace

这里是三个函数，第一个是我们之前学习到的range，他的返回值本质上是一个可迭代对象，可以看作是一个迭代器，而且也有一定的局限性，例如步长只能是整数

第二个是用于创建数组的方法，步长可以是浮点数，而且他的底层其实是C语言，因此执行效率也会比较高，对于arange他的返回值就是数组对象本身了

第三个是也是用于创建数组的方法，他的好处是避免了每一次创建数组都要手动算一下步长，他的参数有三个，起始位置，停止位置，数据个数，例如

arr4 = np.linspace(1,10,20)

其他常用函数

方法	说明	示例
zeros	生成全零数组	ze = zeros((2,3)) 生成两行三列0数组
ones	生成全一数组	与上面一样
shape参数	描述轮廓	one = np.ones(shape = [3, 4], dtype = float)
zeros_like	结构和某数组一样的全零数组	ze1 = zeros_like(ze)
ones_like	结构和某数组一样的全一数组	one = zeros_like(one)

其余函数还有，empty_like、full_like，等等

N维数组的属性

我们首先要知道，内存的本质还是一维的，用狭隘的眼光来看他甚至只能从一个方向存储删除数据，因此我们所说的n维数组实际上是一个逻辑的结构，并非内存的真实结构

一个n维数组的本质就是用n个同类的数据容器来存储数据

我们可以用ndim输出数组的维度

arr1 = np.arange(1,10)
print(arr1.ndim)

同样的，我们也可以用shape查看数组的形状信息

print(arr1.shape)

我们也可以用reshape()方法来改变一维数组的形状信息，也就是重构或者说变形

arr1 = np.arange(1,10)
print(arr1.shape)
print(arr1)
arr2 = arr1.reshape(3,3)
print(arr2.shape)
print(arr2)

需要注意的是，三位数组的形状信息是分别对应着宽、高、长

NumPy数组的运算

向量运算

如果我们想求两个列表元素对应的和，我们可以使用for循环，列表推导式，也可以将他们转换为数组直接求和即可

import numpy as np
arr1 = np.arange(1,11)
arr2 = np.arange(11,21)
arr3 = arr1 + arr2
print(arr1)
print(arr2)
print(arr3)

算数运算

NumPy有着强大的算数运算函数，只需要直接调用即可

如果要进行普通的数学运算，直接跟两个数字直接运算的方法一模一样，支持加减乘除取余乘方

注意，要操作数组的形状一致，除数不要为0就行

还有许多统计函数，例如

函数	说明
sum	求和
min	最小值
max	最大值
median	中位数
mean	平均数
average	加权平均数
std	标准差
var	方差

逐元素运算、点乘运算

N维数组实际上类似于矩阵，一般来说，加减乘除是元素对元素的运算

这里的乘法与矩阵乘法或是向量乘法不同，而是元素对元素的乘法

对于数学中的点乘操作NumPy也有对应的方法为dot()，也可以使用@符号替换乘法操作，意为点乘

例如

arr1 = np.arange(1, 10)
arr2 = np.arange(11, 20)
arr1 = arr1.reshape(3, 3)
arr2 = arr2.reshape(3, 3)
print(arr1*arr2)
print(arr1@arr2)
print(np.dot(arr1,arr2))

后两种符合的就是矩阵乘法的操作了

其他矩阵运算的函数

方法	说明
a.I	返回a的逆矩阵
a.T	返回a的转置矩阵
a.A	返回a对应的二维数组

操作数组元素

索引访问数组

索引是数组中元素所在的编号，类似于列表和C/C++中的数组，像一个指针一样对数组进行访问

一维数组二维数组的访问也是相同的，同样可以更改数组中的值

切片访问数组

与Python的列表一样，NumPy也可以使用切片访问和修改数据，我们可以批量获取符合要求的元素，提取出一个新的数组

例如

arr1 = np.arange(1,10)
sl = slice(2,9,2)
arr2 = arr1[sl]
print(arr2)
print(arr1)

这里的arr1表示原有数组，sl表示切片对象，是利用slice函数构造出来的，代表从2到9，步长为2，再对arr1切片得到arr2

也可以利用类似列表的切片方法arr2 = arr1[2:9:2]

转置与展平

我们可以通过transpose()方法将二维数组转置，也可以通过我们上面提到过的ArrName.T来进行转置

要将多维数组转化成一维数组，就要使用ravel()方法完成这个功能

例如

arr1 = np.arange(1,10)
arr1 = arr1.reshape(3,3)
print(arr1)
arr1 = arr1.T
print(arr1)
arr1 = arr1.ravel()
print(arr1)

flatten()函数也可以进行展平操作，不同的是，flatten会重新分配内存，进行一次深拷贝，但是原数组并没有改变

NumPy的广播

实际上就是对两个数组进行加减乘除运算时，即便两个数组形状不同，NumPy会自动填充小数组中的元素来匹配大数组，这种机制也叫做广播(broadcasting)，这个过程中需要的性能比较小，也无须关注实现细节

NumPy的高级索引

整数索引

这种索引的使用场景是为了补充之前的直接索引和切片索引，一旦我们想要访问的数据没有规律可循，但数据量比较大的时候，我们可以自行指定一个索引表进行访问

例如

import numpy as np
arr1 = np.arange(1,50)
index = [5,23,23,32,37,16]
print(arr1[index])

如果是二维数组，只需要写一个二维索引表即可

需要注意的是，我们也可以只访问行索引和列索引，行索引直接传入一维列表即可，列索引需要用冒号隔开，在冒号之后传入一维列表即为列索引

布尔索引

这里就类似于筛选的功能，符合条件(True)的数据就会被保留下来，不符合则会被过滤

例如

arr1 = np.arange(1,50)
index = [5,23,23,32,37,16]
arr1 = arr1[index]
print(arr1[arr1<30])

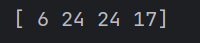
需要注意的是这里的arr1<30实际上就是利用了之前的广播，将30扩展成一个同样形状的数组，然后分别进行比较

数组的堆叠

这里的堆叠可以将数组理解成书，他分为三中，水平方向堆叠，类比两本书横向堆叠放，垂直方向堆叠，就是两本书纵向堆叠，深度方向堆叠就是一本书摞在另一本书上了

水平方向堆叠

hstack()这里的h表示水平，stack表示堆叠，需要注意的是，这个函数的参数是一个元组，元组内的元素可以是列表，数组等，返回结果是一个数组

例如

list1 = [[1,1,2],[3,4,4]]
list2 = [[2,3,3],[4,4,5]]
arr1 = np.hstack((list1,list2))
print(arr1)

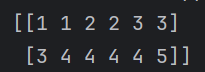
他是把两个元素的前两项叠在一起，后两项叠在一起，之后再组成一个数组

竖直方向堆叠

vstack() 例如

list1 = [[1,1,2],[3,4,4]]
list2 = [[2,3,3],[4,4,5]]
arr1 = np.vstack((list1,list2))
print(arr1)

深度方向堆叠

dstack() 例如

list1 = [[1,1,2],[3,4,4]]
list2 = [[2,3,3],[4,4,5]]
arr1 = np.dstack((list1,list2))
print(arr1)

这里输出的就是一个三维数组了，相当于把两片纸堆叠在一起就有了高度

要注意元素之间的对应关系

行堆叠和列堆叠

这里就好理解很多了，因为上面的三个操作是在三维空间里的堆叠，而这里只是针对二维的数据

行堆叠 column_stack()

列堆叠 row_stack()

数组的分割

分割就是与堆叠的你操作，那也就分为水平分割，垂直分割，深度分割

分别用hsplit(),vsplit(),dsplit()实现

随机数

NumPy中含有随机数模块，random

随机数其实是由随机数种子根据一定规则计算出的数值，因此只要计算方法和种子一定，随机数就是不会变了，如果不设置随机种子，就会根据系统时间生成随机种子

例如

import numpy as nprdm = np.random.RandomState(1)
np.random.seed(20231214) # 定义随机种子# 生成两行三列的随机数组，服从均匀分布
rand = np.random.rand(2,3)
print(rand)# 生成两行三列的随机数组，服从标准正态分布
randn = np.random.randn(2,3)
print(randn)# 生成两行三列的1到10的随机整数
randint = np.random.randint(1,10,(2,3))
print(randint)

感谢各位的支持，如果你发现文章中有任何不严谨或者需要补充的部分，欢迎在评论区指出