Dirichlet Process (徐亦达老师)狄利克雷过程-编程知识

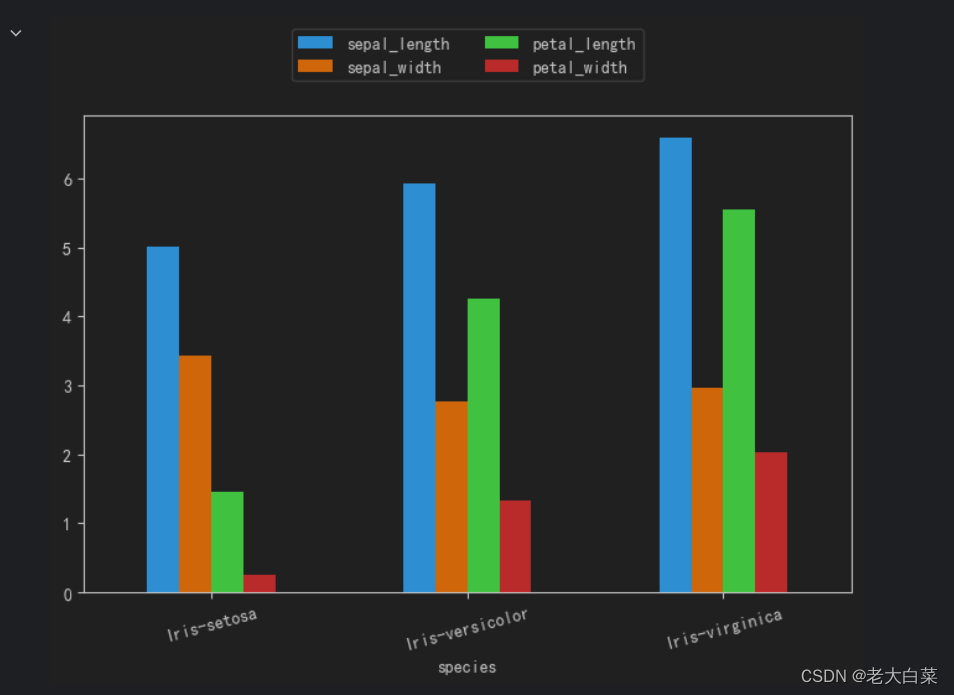
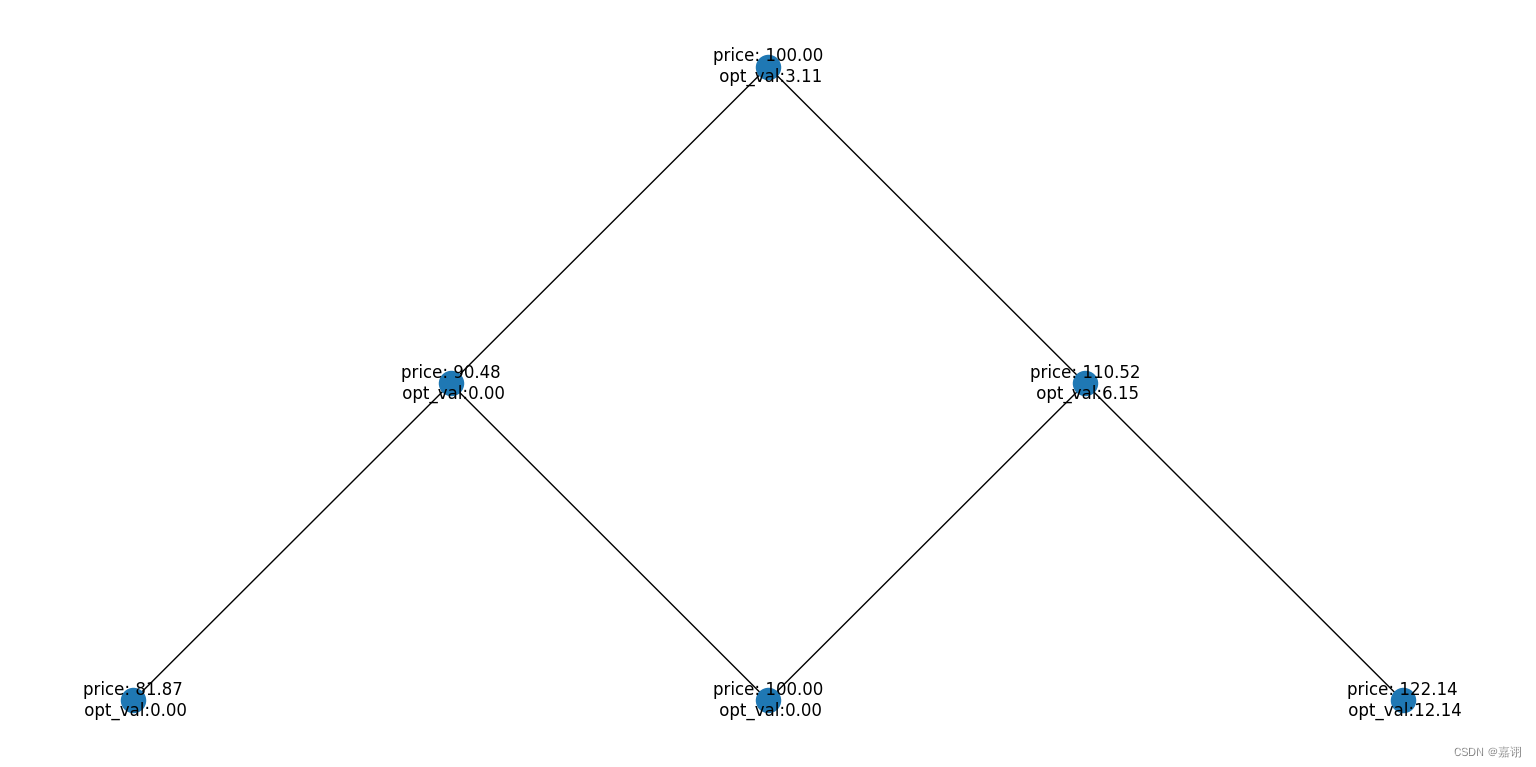
混合高斯模型的例子

混合高斯模型

混合高斯模型（Mixture of Gaussians，简称GMM）是一种概率模型，用于对复杂的数据分布进行建模。它是由多个高斯分布组合而成的混合模型，每个高斯分布（称为组件）对应数据的一个子群体。混合高斯模型的概率密度函数可以表示为多个高斯分布的线性组合，即每个分布乘以一个相应的权重。数学形式如下：

$\sum_{i=1}^{K} \pi_i \cdot \mathcal{N}(x | \mu_i, \Sigma_i)$

其中，K是高斯分布的数量， $\pi_i$ 是对应于第 i 个高斯分布的权重， $\mathcal{N}(x | \mu_i, \Sigma_i)$ 是第i个高斯分布的概率密度函数，由均值 $\mu_i$ 和协方差矩阵 $\Sigma_i$ 参数化。

问题

假设有一堆数据 $X=\{x_1,…，x_N\}$ ,并且假设其采样自一个高斯混合分布，那么如何判断该高斯混合分布中的K值为多少？

最大似然估计（Maximum Likelihood Estimation，MLE） 一种解法是采用最大似然估计，将K作为分布的参数，选择使得观测数据出现的概率最大的参数值。最大似然估计的步骤如下：

建立似然函数： 根据模型和观测数据建立似然函数。
对似然函数取对数： 为了方便计算，通常对似然函数取自然对数。
求导数并令其为零： 对取对数后的似然函数关于参数进行求导，并令导数为零，解得似然方程。
求解似然方程： 解似然方程得到参数的估计值。
检验估计的合理性： 通过检验估计的标准误差、置信区间等来评估估计的精确性和可靠性。

在这里插入图片描述

但是这种方法会得到平凡解 $K = N$ ,均值为数据的值，方差为0。

在这里插入图片描述

思考

如果 $K = N$ ，那么聚类就没有意义了，假设 $K = f (N)$ ,那么函数f应该是什么形式？
答： $\propto log(N)$ ,N增加K也增加，但是K增加的度远小于N。

另一个例子

假设有一堆数据 $X=\{x_1,…，x_N\}$ ,并且假设每个数据都对应一个参数为 $\theta _i$ 的分布并由其产生。 $\theta_i$ 也是从某个分布生成的 $\theta_i \sim H(\theta)$ 。如果H是连续的，那么会有以下的情况出现(红线标注处，如果 $\theta_1，\theta_2$ 采用自一个连续的分布，那么二者相等的概率为0，那么所有的几个 $\theta$ 值都不相等，K还是等于N，所以H是非连续分布。

在这里插入图片描述
假设 $\theta$ 从G中产生， $\theta _i\sim G$ ，但是G和H是有联系的， $\color{red} G\sim DP(\alpha,H)$ ，其中 $\alpha$ 是一个程度标量，描述G的离散程度， $\alpha$ 越小G越离散， $\alpha$ 越大，G越连续。 $\alpha=0$ 时G只有一个点， $\alpha=\infty$ 时 $G = H$ 。

在这里插入图片描述

狄利克雷过程

从 $\color{red} G\sim DP(\alpha,H)$ 中每次采样得到的都是一个分布，但是这些分布是有某种特性的。

在这里插入图片描述

迪利克雷分布DIR

G的划分性质 假设将分布的定义域进行划分，划分成d个区域，在第i个区域 $a_i$ ,G在 $a_i$ 上权重的总和 $G(a_i)$ 有如下性质(红线部分)：

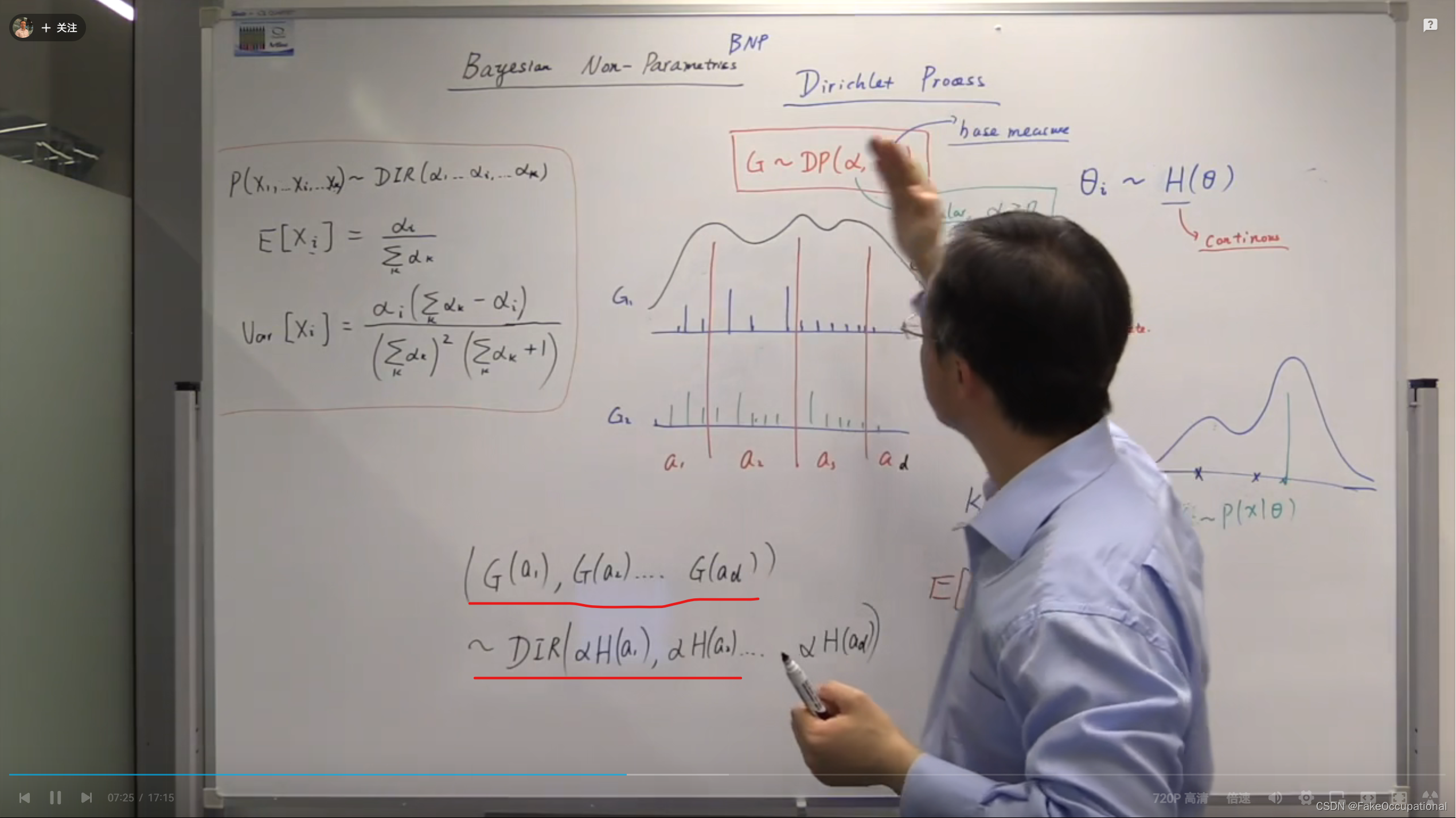
在这里插入图片描述

其中DIR为狄利克雷分布（Dirichlet distribution,红框中为DIR分布的特性）：

$f(\mathbf{x};\boldsymbol{\alpha}) = \frac{1}{B(\boldsymbol{\alpha})} \prod_{i=1}^{K} x_i^{\alpha_i - 1}$

其中：

$\mathbf{x} = (x_1, x_2, \ldots, x_K)$ 是一个K维随机变量，满足 $\leq x_i \leq 1$ 和 $\sum_{i=1}^{K} x_i = 1$ 。
$\boldsymbol{\alpha} = (\alpha_1, \alpha_2, \ldots, \alpha_K)$ 是分布的参数，其中每个 $\alpha_i > 0$ 。狄利克雷分布的参数 $\boldsymbol{\alpha}$ 可以影响分布的形状。当所有的 $\alpha_i$ 都相等时，分布是均匀的；当某些 $\alpha_i$ 大于1而其他的小于1时，分布会偏向于在对应的维度上取较大的值。
$B(\boldsymbol{\alpha})$ 是多元Beta函数，定义为 $B(\boldsymbol{\alpha}) = \frac{\prod_{i=1}^{K} \Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^{K} \alpha_i)}$ ，其中 $\Gamma$ 是伽玛函数。

在这里插入图片描述
因为G在划分上服从迪利克雷分布，又因为红框中的性质：

$E[G(a_i)]=\frac{\alpha H(a_i)}{\sum_k \alpha H(a_k)} = \frac{\alpha H(a_i)}{ \alpha \sum_kH(a_k)} = \frac{\alpha H(a_i)}{ \alpha \cdot 1} = H(a_i)$

$Var[G(a_i)]=\frac{H(a_i)(1-H(a_i))}{\alpha+1}$

$\alpha\rightarrow \infty ,Var[G(a_i)]=0$
$\alpha\rightarrow 0, Var[G(a_i)]={H(a_i)(1-H(a_i))},二项分布$

G的折棍构造 stick-breaking constructin

如何从分布中采样G？G长什么样？ $G=\sum_{i=0}^{\infty}\pi_i\delta\theta_i$

采样第一个点

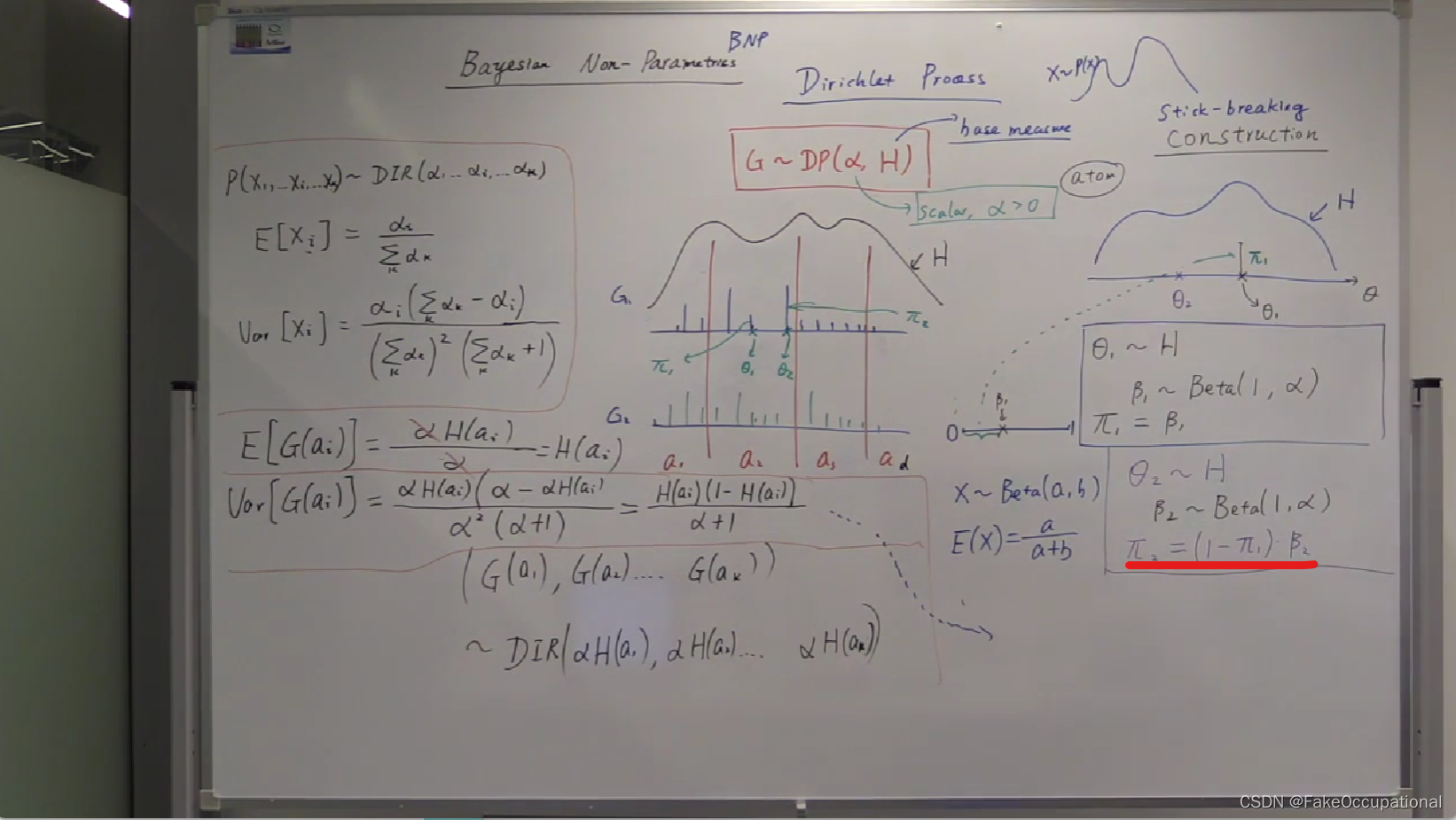
在这里插入图片描述

采样第二个点， $(1-\pi_1)$ 为第一次采样后剩下的，者剩下的

在这里插入图片描述

在采样完所有这些点之后就得到一个G的visualization。因为 $\beta_i\sim Beta(1,\alpha),所以E[\beta_i]=\frac{1}{1+\alpha}$ 。当 $\alpha=0,E[\beta_i]=1$ 。当 $\alpha=\infty,E[\beta_i]=0$ ，即产生了0各权重给每个 $\theta$ 用。

小结

G的后验

假设已经知道了了 $\theta_1,\theta_2,……，\theta_N$ 。
$P(G|\theta_1,\theta_2,……，\theta_N) = P(\theta_1,\theta_2,……，\theta_N|G)\times P(G) = G\times P(G)$

和多项式分布的关系

如果将狄利克雷分布的参数α 视为多项式分布中的概率参数p 的先验分布，那么在贝叶斯统计学中，给定观测数据，通过贝叶斯公式可以更新参数的后验分布。这个后验分布将是一个狄利克雷分布。这表明狄利克雷分布是多项式分布的共轭先验。

多项式分布

多项式分布（Multinomial Distribution）是概率论和统计学中的一种离散概率分布，它是二项分布的推广。在多项式分布中，试验的结果有两个以上的分类，每个分类有一个概率，且这些概率之和为1。与二项分布不同，多项式分布描述的是多个试验中各个分类的次数。

考虑一个试验，将一个对象放入多个互不相交的类别中，每个类别发生的概率为 $p_1, p_2, \ldots, p_k$ ，其中 $p_i$ 表示对象属于第 $i$ 个类别的概率。试验进行了 $n$ 次，我们想知道每个类别发生的次数。

多项式分布的概率质量函数为：

$P(X_1 = x_1, X_2 = x_2, \ldots, X_k = x_k) = \frac{n!}{x_1! \cdot x_2! \cdot \ldots \cdot x_k!} \cdot p_1^{x_1} \cdot p_2^{x_2} \cdot \ldots \cdot p_k^{x_k}$

其中：

$n$ 是试验次数。
$k$ 是类别的个数。
$x_1, x_2, \ldots, x_k$ 分别是每个类别发生的次数。
$p_1, p_2, \ldots, p_k$ 分别是每个类别发生的概率，且 $\sum_{i=1}^{k} p_i = 1$ 。

多项式分布常常用于描述具有多个离散类别的随机试验，例如扔骰子、抽取彩球等。

似然为多项式分布

在这里插入图片描述

中国餐馆过程

predictive distribution

在这里插入图片描述

CG

https://github.com/sakshamgarg/Dirichlet-Out-of-Distribution-Detection
https://www.cs.princeton.edu/courses/archive/fall07/cos597C/scribe/20070921.pdf

SAM

安装

https://github.com/facebookresearch/segment-anything#model-checkpoints

$ pip install git+https://github.com/facebookresearch/segment-anything.git
Looking in indexes: https://pypi.tuna.tsinghua.edu.cn/simple
Collecting git+https://github.com/facebookresearch/segment-anything.gitCloning https://github.com/facebookresearch/segment-anything.git to /tmp/pip-req-build-3od4d54tRunning command git clone --filter=blob:none --quiet https://github.com/facebookresearch/segment-anything.git /tmp/pip-req-build-3od4d54tResolved https://github.com/facebookresearch/segment-anything.git to commit 6fdee8f2727f4506cfbbe553e23b895e27956588Preparing metadata (setup.py) ... done
Building wheels for collected packages: segment-anythingBuilding wheel for segment-anything (setup.py) ... doneCreated wheel for segment-anything: filename=segment_anything-1.0-py3-none-any.whl size=36589 sha256=b23a3b85adc5d579423f8ef9a218af802032d60d6aa3706d67f87dbe48d70fd5Stored in directory: /tmp/pip-ephem-wheel-cache-119odynp/wheels/b0/7e/40/20f0b1e23280cc4a66dc8009c29f42cb4afc1b205bc5814786
Successfully built segment-anything
Installing collected packages: segment-anything
Successfully installed segment-anything-1.0

使用

从给定的提示中获取掩码

from segment_anything import SamPredictor, sam_model_registry
sam = sam_model_registry["vit_l"](checkpoint="sam_vit_l_0b3195.pth")
predictor = SamPredictor(sam)
predictor.set_image(<your_image>)
masks, _, _ = predictor.predict(<input_prompts>)

为整个图像生成蒙版

from segment_anything import SamAutomaticMaskGenerator, sam_model_registry
sam = sam_model_registry["vit_l"](checkpoint="sam_vit_l_0b3195.pth")
mask_generator = SamAutomaticMaskGenerator(sam)
masks = mask_generator.generate(<your_image>)