JavaScript版数据结构与算法（一）栈、队列、链表、集合、树

一、前言

为什么要学习数据结构与算法？最重要的就是面试要考算法，另外就是如果在实际工作当中，能够使用算法优化代码，会提升代码质量和运行效率，作为一名前端人员可能在实际中用的并不是特别多。数据结构与算法是分不开的，数据结构是计算机存储、组织数据的方式，算法是一系列解决问题的清晰指令，程序就是数据结构＋算法。算法刷题大家都知道，就是力扣。刷题顺序推荐按类型刷题，比如栈相关的题，一次刷好几道，巩固巩固。刷题过程中需要重点关注的是通用套路、时间/空间复杂度分析和优化。其实这跟高中初中做数学题很像，有通用的套路可循，但是需要多复习，多看错题，做题的时候尽量把这道题考察的知识点都总结出来。
要学习的数据结构大致分为下面几类：

  • 有序：栈、队列、链表
  • 无序：集合、字典
  • 有相互连接关系：树、堆（特殊的树）、图

学习的算法大致分为下面几类：

  • 链表：遍历链表、删除链表节点。
  • 树、图：深度/广度优先遍历。
  • 数组：冒泡/选择/插入/日并/快速排序、顺序/二分搜索。

关于时间复杂度：
用O()函数表示，定性描述算法运行时间

  • O(1)
    代码只会执行一次，没有任何循环
    let i = 1;
i += 1;
  • O(n)
    for循环中的代码会执行n次
    for (let i = 0; i < n; i += 1) {console. log(i);
}
  • O(1) + O(n) = O(n)
    代码上下顺序执行是两个时间复杂度相加，只算增长趋势较大的时间复杂度，增长趋势较小的时间复杂度可以忽略
    let i = 1;
i += 1;
for (let j = 0; j < n; j += 1) {console. log(i);
}
  • O(n) * O(n) = O(n^2)
    两个方法嵌套的时间复杂度需要两个时间复杂度相乘
    for (let i=0;i<n;i+=1){for (let j = 0; j < n; j += 1) {console. log(i, j);}
}
  • O(logN)
    let i = 1;
while(i < n){console.log(i);i *= 2;
}

空间复杂度
用O()函数表示
算法在运行过程中临时占用存储空问大小的量度，越小越好

  • O(1)
    只有一个变量
    let i = 0；
i += 1
  • O(n)
    在内存中声明了n个变量
    const list = [];
for (let i=0; i<n;i+=1){list.push(i);
}
  • O(n^2)
    就是一个矩阵
    const matrix = [];
for(let i = 0;i < n;i += 1){matrix.push([])for(let j=0; j<n; j +=1){matrix[i].push(j)}
}

二、栈

栈就是一个后进先出的数据结构
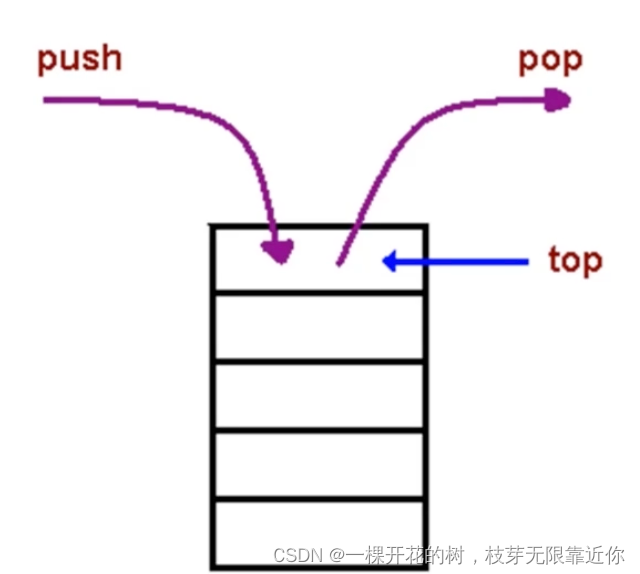
在这里插入图片描述
javascript中没有栈这种数据结构，但是可以用Array实现栈，模仿栈的操作。

const stack = [];
// 入栈
stack.push(1);
stack.push(2);
// 出栈
// pop()将最后的元素删除，并且返回
const item1 = stack.pop()
console.log(item1)
// 出栈
const item2 = stack.pop()
console.log(item2)

什么场景下用栈？
所有后进先出的场景，例如：

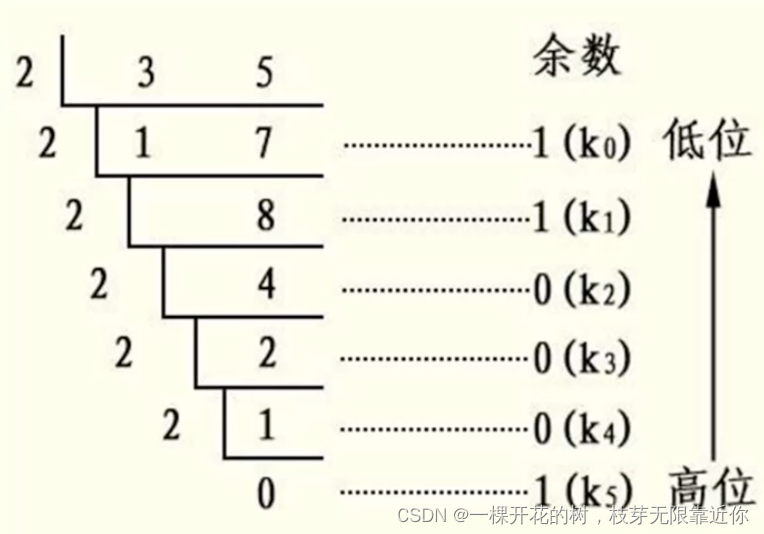
  • 十进制转二进制
    需要用十进制数不断除以2，并且倒序取余数，后算出的余数要排在前面，因此可以将余数依次存入栈中，再出栈，就可以实现余数倒序输出
    在这里插入图片描述
/*** 十进制转二进制* */
// 1、数字除以2 得到商和余数
// 2、余数push到栈中
// 3、商继续除以2 得商和余数
// 4、余数继续入栈
const trans = function (num) {const stack = []let n = num;while (n > 0) {// 获取商const shang = Math.floor(n / 2);// 获取余数const yushu = n % 2;// 余数入栈stack.push(yushu);// n重新赋值n = shang;}return stack.reverse().join('')
}

  • 判断字符串的括号是否有效
    在敲代码的时候，代码编辑器经常要判断括号是否正常闭合，无效的括号会给我们错误提示。这个算法就是编辑器中常用的判断括号是否有效的算法。
    越靠后的左括号，对应的右括号越靠前。
    左括号入栈，右括号出栈，最后栈空了就是合法的。
    在这里插入图片描述

  • 函数调用堆栈
    最后调用的函数，是最先执行完的
    greeting() start -> [1] 操作 -> sayHi() start -> sayHi() end -> [2] 操作 -> greeting() end -> [3] 操作
    JS解释器使用栈来控制函数的调用顺序。
    在这里插入图片描述

三、队列

先进先出
javascript中没有队列，但能用数组实现队列

// 创建队列
const queue = [];
// 入队
queue.push(1)
queue.push(2)
// 出队
const item1 = queue.shift()
console.log(item1)
const item2 = queue.shift()
console.log(item2)

应用场景：
所有先进先出的场景
食堂打饭
js异步任务队列（事件循环）
异步任务会放在任务队列中，先放进队列的先执行
计算最近请求次数

四、链表

多个元素组成的链表
但是元素存储不连续，用 next 指针连在一起。

数组 VS 链表
数组：增删非首尾元素时往往需要移动元素。
链表：增删非首尾元素，不需要移动元素，只需要更改 next 的指向即可。

javascript中可以用 object 模拟链表

前端中的链表–原型链
原型链的本质是链表。
原型链上的节点是各种原型对象，比如Function.prototype, Object.prototype…
原型链通过_proto_属性连接各种原型对象。
原型链知识点
如果 A 沿着原型链能找到 B.prototype，那么A instanceof B 为true。
如果在 A 对象上没有找到x 属性，那么会沿着原型链找 x 属性。
面试题一
instanceof 的原理，并用代码实现。

// 如果 A 沿着原型链能找到 B.prototype，那么A instanceof B 为true。
function instanceOf(A, B){let p = A;while(p){if(p == B.prototype) return true;p = p.__proto__;}return false;
}

五、集合

集合是一种无序且唯一的数据结构。
栈、队列、链表都是有序的数据结构，并且元素都是可以重复的。
前端中的集合: Set
常用操作：
数组去重
[...new Set([1, 2, 3, 1, 2])]
判断某元素是否在集合中
set.has(3)
求两个集合的交集

const set = new Set([1,2,3,2,1])
const set2 = new Set([2,3,4])
// 筛选出set中有，并且set2里面也有的元素
const set3 = new Set([...set].filter(s=>set2.has(s)))
console.log(set3)

字典
与集合类似，字典也是一种存储唯一值的数据结构，但它是以键值对的形式来存储。
ES6 中有字典，名为 Map。
字典的常用操作：键值对的增删改查。

// 增删改查
const m = new Map();
m.set('a', 'aa')
m.set('b', 'bb')
m.delete('b')
// 清空
// m.clear();
// 改直接覆盖set
m.set('a', '啊啊')// 求两个数组中都存在的元素，要求去重
const arr1 = [1,2, 2,3,4]
const arr2 = [2,3,2,4]
// 字典中的key也是唯一的，所以遍历数组一创建字典就不会有重复的key
const map = new Map();
arr1.forEach(a=>{map.set(a, true)
})
const res = []
arr2.forEach(a=>{if(map.get(a)) {res.push(a)map.delete(a)}
})
console.log(res)

六、树

树是一种分层数据的抽象模型
前端的树：DOM树、级联选择、树形控件
JS中没有树，只能用Array和Object模拟
树的常用操作：深度/广度优先遍历、二叉树的先中后序遍历。
深度优先遍历：尽可能深的搜索树的分支
广度优先遍历：先访问离根节点最近的节点
下面一图，左侧是深度优先遍历的访问顺序，右侧是广度优先遍历的访问顺序
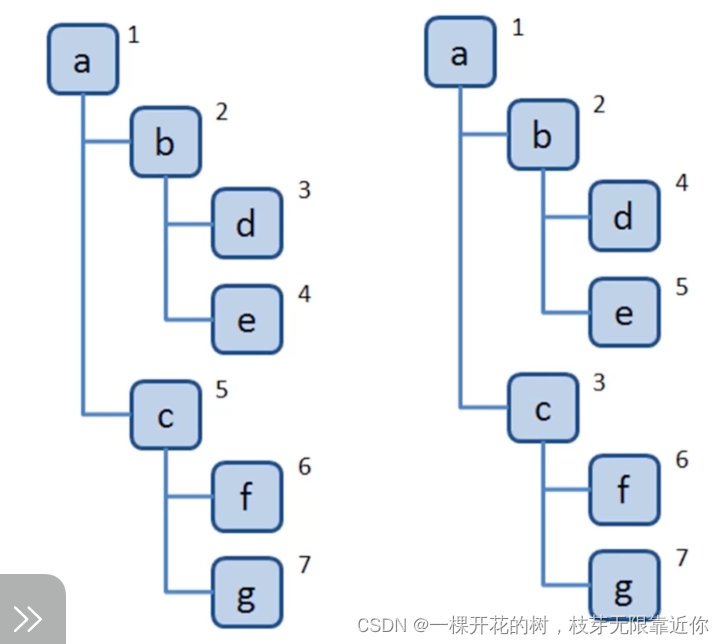
在这里插入图片描述
深度优先遍历算法口诀 （最为重要）
1、访问根节点
2、对根节点的 children 挨个进行深度优先遍历。

// 深度优先遍历
const tree={val: 'a',children:[{val: 'b',children:[{val: 'd',children:[]},{val: 'e',children:[]}]},{val: 'c',children:[{val: 'f',children:[]},{val: 'g',children:[]}]}]
}const dfs = (root) =>{// 访问根节点console.log(root);// 对根节点的children依次进行深度优先遍历root.children.forEach(dfs);
}console.log(dfs(tree))

广度优先遍历算法口诀
1、新建一个队列，把根节点入队。
2、把队头出队并访问。
3、把队头的 children 挨个入队。
4、重复第二、三步，直到队列为空。

// 广度优先遍历
const tree = {val: 'a',children: [{val: 'b',children: [{val: 'd',children: []},{val: 'e',children: []}]},{val: 'c',children: [{val: 'f',children: []},{val: 'g',children: []}]}]
}
const bfs = (root) => {// 新建一个队列 根节点入队const q = [root]while (q.length > 0) {// 队头出队并访问const n = q.shift();console.log(n)// 队头的children挨个入队n.children.forEach(c => q.push(c));}
}
bfs(tree)

树在前端中的应用

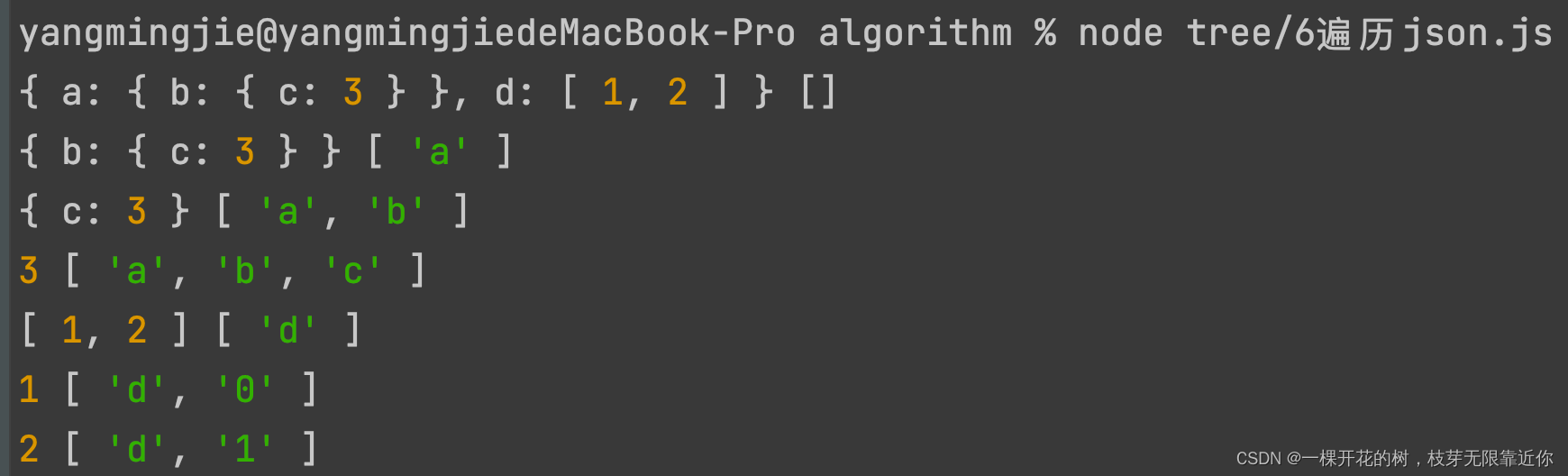
  • 访问json数据中的所有节点
    使用深度优先遍历实现，深度优先遍历就是先访问根节点，然后对每个根节点进行深度优先遍历
// 访问json中所有节点值
const json = {a: {b: {c: 3}},d: [1, 2]
}// 深度优先遍历 使用path记录每个节点的路径
const dfs = (n, path) =>{// 访问当前节点console.log(n, path)// 使用Object.keys遍历n的所有子节点Object.keys(n).forEach(k=>{dfs(n[k], path.concat(k))})
}dfs(json, [])

在这里插入图片描述

七、二叉树

树中每个节点最多只能有两个子节点。
在JS中通常用 Object 来模拟二叉树。

const binaryTree = {val: '1',left: {val: '2',left: null,right: null},right: {val: '3',left: null,right: null}
}

二叉树的遍历主要有三种：先序遍历、中序遍历、后序遍历
二叉树的先序遍历
根->左->右
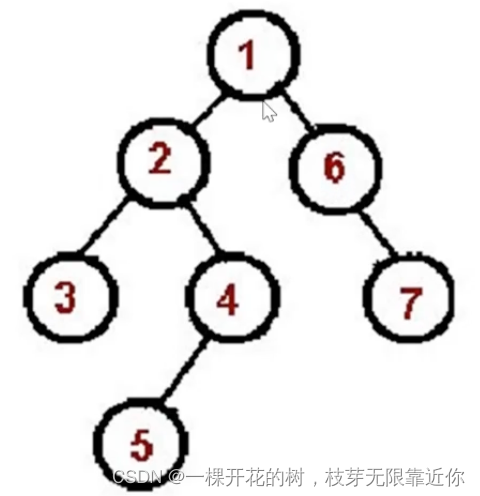
在这里插入图片描述

1、访问根节点。
2、对根节点的左子树进行先序遍历。
3、对根节点的右子树进行先序遍历。

const binaryTree = {val: '1',left: {val: '2',left: {val: '4',left: null,right: null},right: {val: '5',left: null,right: null}},right: {val: '3',left: {val: '6',left: null,right: null},right: {val: '7',left: null,right: null}}
}const preorder = root => {if (!root) return;console.log(root.val);preorder(root.left);preorder(root.right);
}
preorder(binaryTree)

二叉树的中序遍历
左->根->右
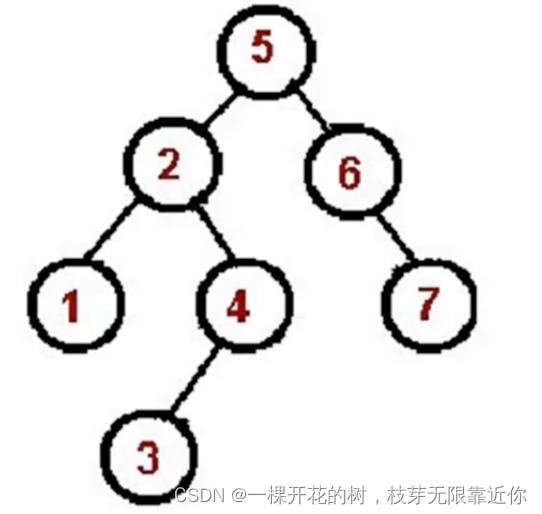
在这里插入图片描述
1、对根节点的左子树进行中序遍历。
2、访问根节点。
3、对根节点的右子树进行中序遍历。
首先对于整棵树而言，根节点是5，要先对于左子树2进行中序遍历，找2 的左子树，是1，对1中序遍历，1没有左子树，所以1是最先访问的节点
当前节点是1，访问1的根节点，就是2，第二个访问的是2
然后对2这棵树的右子树进行中序遍历，即4，先找4的左子树，即3，访问3，即第三个访问的是3
3访问完，要访问3的根节点，第四个访问的是4
4没有右子树，所以结束访问，2也结束了访问
此时就要访问2节点所在的根节点，即5，第五个访问的是5
在找5的右子树，进行中序遍历，它的右子树6没有左子树，所以先访问根节点6，即第六个访问的是6
访问6之后需要访问6树的右子树，即7，因此第七个访问的是7

二叉树的后序遍历
左->右->根
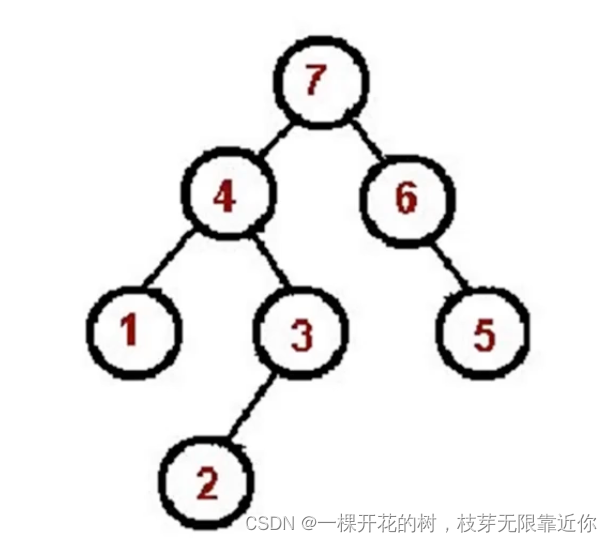
在这里插入图片描述
1、对根节点的左子树进行后序遍历。
2、对根节点的右子树进行后序遍历。
3、访问根节点。

// 将二叉树定义为一个独立可复用的模块
const binaryTree = require('./binaryTree')
const postorder = (root) => {if (!root) return;// 1 左子树进行后序遍历postorder(root.left);// 2 右子树进行后序遍历postorder(root.right);// 3 访问根节点console.log(root.val);
}
postorder(binaryTree)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/333714.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

4.6 BOUNDARY CHECKS

4.6 BOUNDARY CHECKS

我们现在扩展了tile矩阵乘法内核&#xff0c;以处理具有任意宽度的矩阵。扩展必须允许内核正确处理宽度不是tile宽度倍数的矩阵。通过更改图4.14中的示例至33 M、N和P矩阵&#xff0c;图4.18创建了矩阵的宽度为3&#xff0c;不是tile宽度&#xff08;2&#xff09;的倍数。图4.…
阅读更多...
AI红娘开启约会新时代；网易云音乐Agent实践探索；微软生成式AI课程要点笔记；ComfyUI新手教程；图解RAG进阶技术 | ShowMeAI日报

AI红娘开启约会新时代；网易云音乐Agent实践探索；微软生成式AI课程要点笔记；ComfyUI新手教程；图解RAG进阶技术 | ShowMeAI日报

&#x1f440;日报&周刊合集 | &#x1f3a1;生产力工具与行业应用大全 | &#x1f9e1; 点赞关注评论拜托啦&#xff01; &#x1f440; Perplexity 官宣 7360 万美元B轮融资&#xff0c;打造世界上最快最准确的答案平台 https://blog.perplexity.ai/blog/perplexity-rais…
阅读更多...
用js做点击切换携程旅游

用js做点击切换携程旅游

样式&#xff1a; <style>.domestic {width: 1200px;margin: 50px auto;}.domestic span {padding: 2px 10px;margin: 10px 10px;border-radius: 12px;cursor: pointer;float: left;border: 1px solid transparent;}.domestic > div span:hover {border-color: #f66;b…
阅读更多...
Gartner发布2024年SASE融合战略路线图

Gartner发布2024年SASE融合战略路线图

向云计算和远程工作的转变增加了 SASE 需求&#xff0c;以实现从任何设备的安全访问。安全和风险管理领导者必须将网络和安全融合到一两个明确合作的 SASE 供应商产品中&#xff0c;并淘汰遗留的边界系统。 主要发现 安全访问服务边缘 (SASE) 框架为混合劳动力以及设备、分支机…
阅读更多...
QML —— 示例 - Component自定义组件及加载（附完整源码）

QML —— 示例 - Component自定义组件及加载（附完整源码）

示例效果 介绍 Component 组件是可重用的、封装的QML类型&#xff0c;具有定义良好的接口。组件通常由组件文件定义&#xff0c;即.qml文件。组件类型本质上允许在QML文档中内联定义QML组件&#xff0c;而不是作为单独的QML文件。这可能有助于重用QML文件中的小组件&#xff0c…
阅读更多...
Spring MVC(day1)

Spring MVC(day1)

什么是MVC MVC是一种设计模式&#xff0c;将软件按照模型、视图、控制器来划分&#xff1a; M&#xff1a;Model&#xff0c;模型层&#xff0c;指工程中的JavaBean&#xff0c;作用是处理数据 JavaBean分为两类&#xff1a; 一类称为数据承载Bean&#xff1a;专门存储业务数据…
阅读更多...
Vue-4、单向数据绑定与双向数据绑定

Vue-4、单向数据绑定与双向数据绑定

1、单向数据绑定 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>数据绑定</title><!--引入vue--><script type"text/javascript" src"https://cdn.jsdelivr.net/npm/…
阅读更多...
Linux下安装JET2

Linux下安装JET2

0. 说明&#xff1a; JET2是一个基于Joint Evolutionary Trees的利用序列和结构信息预测蛋白质界面的软件&#xff0c;详情见: http://www.lcqb.upmc.fr/JET2/JET2.html&#xff0c;http://www.lgm.upmc.fr/JET/JET.html 和 https://doi.org/10.1371/journal.pcbi.1004580 本…
阅读更多...
老鸟总结，性能测试-常用指标/指标评估及/通过标准（超级细）

老鸟总结，性能测试-常用指标/指标评估及/通过标准（超级细）

目录&#xff1a;导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结&#xff08;尾部小惊喜&#xff09; 前言 1、性能压测–常用…
阅读更多...
求求你，别再乱用@Transactional了

求求你，别再乱用@Transactional了

求求你&#xff0c;别再乱用Transactional了 文章目录 &#x1f50a;先看个问题&#x1f4d5;情况1情况1结果 &#x1f5a5;️情况2情况2结果 &#x1f4dc; 情况三情况3结果 &#x1f4d8;情况4情况4结果 &#x1f516;先说结论情况1结果情况2结果情况3结果情况4结果&#x1f…
阅读更多...
Linux查看物理CPU个数、核数、逻辑CPU个数

Linux查看物理CPU个数、核数、逻辑CPU个数

文章目录 总核数总逻辑CPU数查看物理CPU个数查看每个物理CPU中core的个数(即核数)查看逻辑CPU的个数 总核数 总核数 物理CPU个数 X 每颗物理CPU的核数 总逻辑CPU数 总逻辑CPU数 物理CPU个数 X 每颗物理CPU的核数 X 超线程数 查看物理CPU个数 cat /proc/cpuinfo| grep “…
阅读更多...
探讨JS混淆技术及其加密解密实例

探讨JS混淆技术及其加密解密实例

引言 在当前计算机科学领域中&#xff0c;保护软件代码的安全性和隐私性变得愈发重要。为了防止黑客攻击和恶意软件分析&#xff0c;开发人员采用各种技术来混淆和加密其代码&#xff0c;其中包括JS混淆技术。本文将介绍JS混淆技术的原理和应用&#xff0c;并提供一些相关的加密…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023