Problem: 1143. 最长公共子序列
文章目录
- 题目描述
- 思路
- 解题方法
- 复杂度
- Code
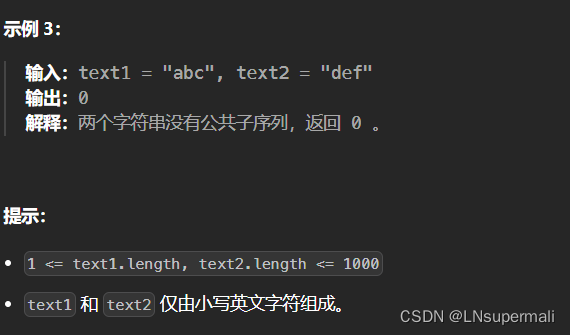
题目描述
思路
我们先假设已经将两个字符串转换为两个char类型的数组(t1,t2)便于比较
1.如果t1[i] == t2[j],有三种决策:(i+1,j+1),(i+1, j), (i, j+1); (i,j表示当前待比较的字符;"i+1"即表示指向t1数组中的一字符的下一个)
如果t1[i] != t2[j],有三种决策:(i+1,j+1),(i+1, j), (i, j+1);
2.达到(i,j)这个状态,也就是说:开始匹配t1[i]和t2[j]了,只可能从上一个阶段的这几个阶段转移过来:(i-1, j),(i, j-1), (i - 1, j - 1);如果状态时(i-1,j),那么i+1,j不变,则得到(i,j)这个状态;
如果状态时(i,j-1),那么i不变,j+1,则得到(i,j)这个状态;
如果状态时(i-1,j-1),那么i+1,j+1,则得到(i,j)这个状态;
3.int dp[n + 1][m + 1];(其中n表示字符串text1的长度,m表示字符串text2的长度);
dp[i][j]表示长度为i的text1的子串和长度为j的text2的子串的最长公共子序列的长度
4.状态转移方程:如果t1[i - 1] == t2[j - 1]则dp[i][j] = max(dp[i - 1][j - 1] + 1, dp[i - 1][j], dp[i][j - 1]);即表示若当前上一个位置的字符相等则其对应的状态存储的最长公共子序列加一(dp[i - 1][j - 1] + 1);如果t1[i - 1] != t2[j - 1]则dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]);
解题方法
1.获取字符串text1和text2的长度text1Len和text2Len,并创建为对应的char类型数组t1和t2;生成二维数组dp:vector<vector> dp(text1Len + 1, vector(text2Len + 1));
2.初始化dp数组的第0行与第0列为0;
3.编写返回给定三个数中最大值的函数
4.从第一行开始执行动态转移方程
5.返回dp[text1Len][text2Len]
复杂度
时间复杂度:
O ( N M ) O(NM) O(NM);其中 N N N为字符产text1的长度, M M M为字符串text2的长度
空间复杂度:
O ( N M ) O(NM) O(NM)
Code
class Solution {
public:/*** Find the longest common subsequence* @param text1 Given string* @param text2 Given string* @return int*/int longestCommonSubsequence(string text1, string text2) {int text1Len = text1.length();int text2Len = text2.length();char *t1 = new char[text1Len + 1];char *t2 = new char[text2Len + 1];strcpy(t1, text1.c_str());strcpy(t2, text2.c_str());//dp[i][j] represents the LCS of// text1[0-i-1](substring of length i)// and text2[0-j-1](substring of length j)vector<vector<int>> dp(text1Len + 1, vector<int>(text2Len + 1));for (int j = 0; j <= text2Len; ++j) {dp[0][j] = 0;}for (int i = 0; i <= text1Len; ++i) {dp[i][0] = 0;}for (int i = 1; i <= text1Len; ++i) {for (int j = 1; j <= text2Len; ++j) {if (t1[i - 1] == t2[j - 1]) {dp[i][j] = max3(dp[i - 1][j - 1] + 1, dp[i - 1][j], dp[i][j - 1]);} else {dp[i][j] = max3(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]);}}}return dp[text1Len][text2Len];}private:/***Find the largest of the three numbers* @param a Figure to be compared* @param b Figure to be compared* @param c Figure to be compared* @return int*/int max3(int a, int b, int c) {int maxVal = a;if (maxVal < b) {maxVal = b;}if (maxVal < c) {maxVal = c;}return maxVal;}
};