10_机械臂运动学_机械臂C++逆解—

就是算！

遨博机械臂改进DH参数表：

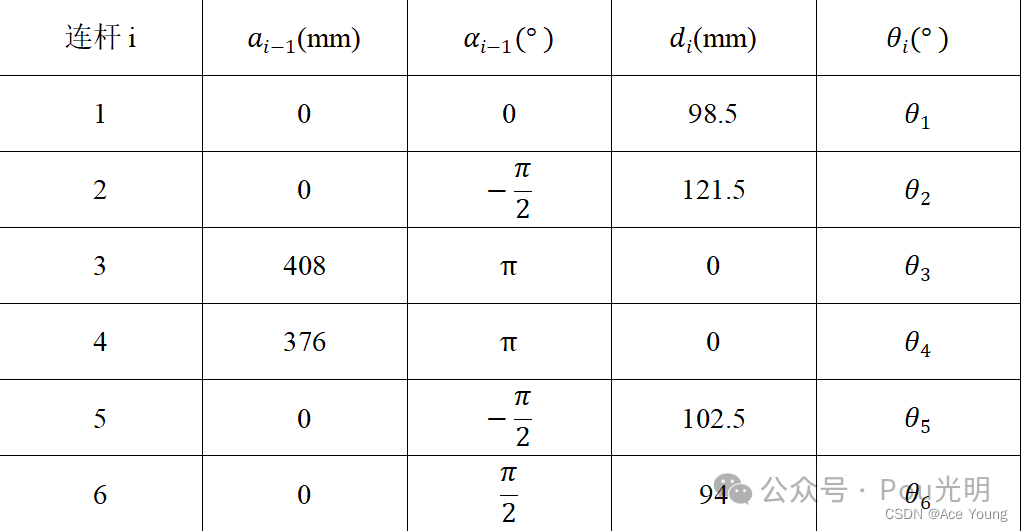
机械臂正运动学连杆变换通式：

其中s_i代表sin(θ_i),c_i代表cos(θ_i)

s_i_j代表sin(θ_i-θ_j),c_i_j代表cos(θ_i-θ_j)

s_i_jk代表sin(θ_i-θ_j+θ_k),c_i_jk代表cos(θ_i-θ_j-+θ_k)，用两角和差公式直接展开即可.

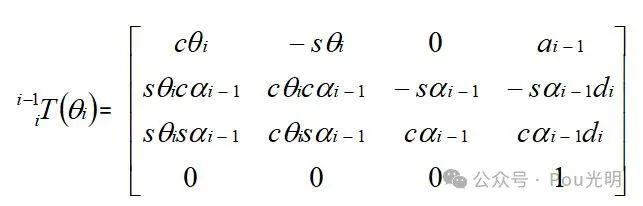
每一个连杆变换矩阵：

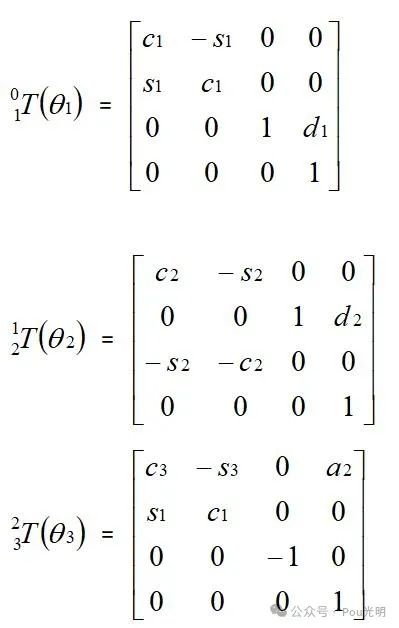
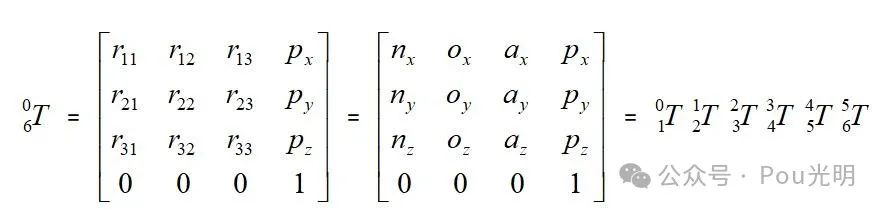
⁰₆T中第四列的前三行数据就是机器人末端连杆在笛卡儿坐标系里的位置参数，前面3*3矩阵表示姿态。

则：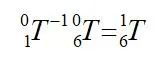

矩阵关系式构建按照《机器人学导论》中的流程：

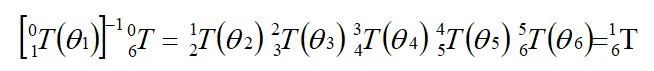
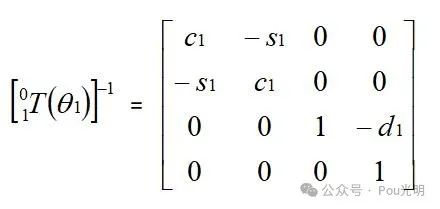
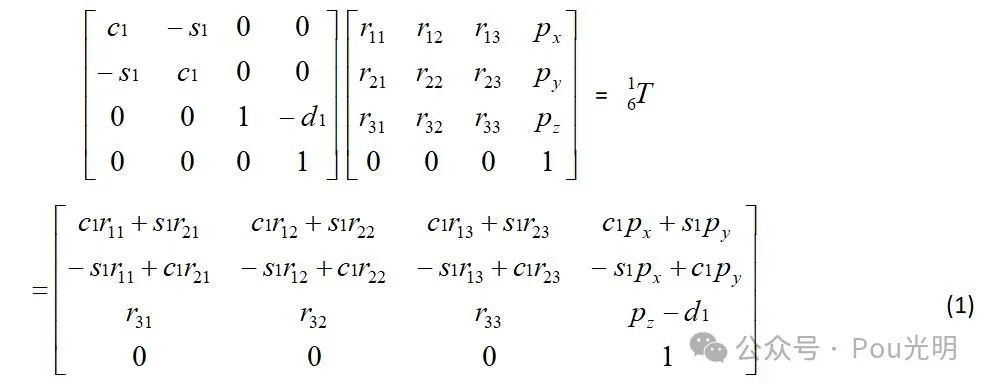
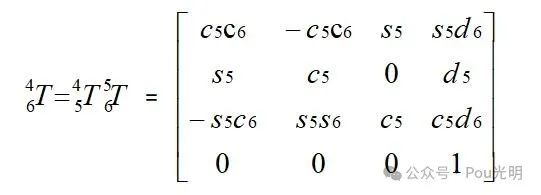
因为关节2和关节3通常是平行的，所以和的乘积用二角和差公式将得到一个简化的表达式。只要两个旋转关节轴平行就可以这样处理，则：

则：

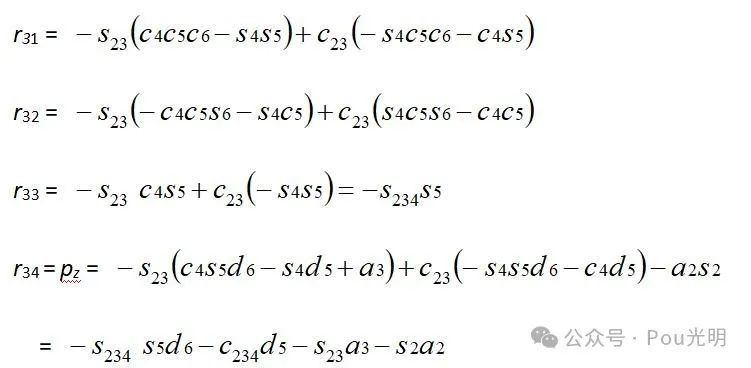
上式构成了aubo机械臂的运动学方程。它们说明如何计算机器人坐标系{6}相对于坐标系{0}的位姿。上述方程式是aubo机械臂全部运动学分析的基本方程。

计算前公式准备：

-As1 + Bc1 = C (3)

解该类型方程通常用三角换元，即：

A =ρcosφ

B =ρsinφ

Φ = atan2(B,A )

则：

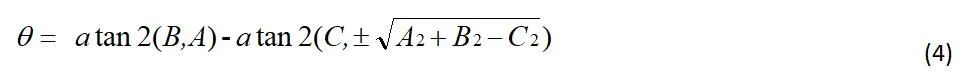
注意，该式有两个解。

sinθ = A

cosθ = B

则：

θ = atan2(A, B) (5)

上述准备工作完成后，下面就是解方程计算，体力活，没啥技巧。

求解θ1：

根据(1)第二行第四列与r24相等，则：

-s1px + c1py = c5d6 + d2

根据(2),c5=r23,

c5 = -s1ax + c1ay,消去c5,

-(px - axd6)s1 + (py - d6ay) = d2 (6)

A = px - axd6

B = py - d6ay

C = d2

再根据(3),直接使用(4),则θ1可解且有两种可能。

求解θ5：

根据(1)第二行第三列与r23相等，则：

-s1ax + c1ay = c5

则：

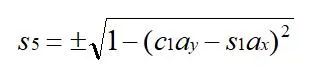
带入公式(5),则：

θ5也有两个解，此时有4组理论解了。

求解θ6：

根据(1)第二行第一列与r21相等，则：

-s1nx + c1ny = -s5c6

根据(1)第二行第二列与r31相等，则：

-s1ox + c1oy = s5s6

由于s1c1s5已知,根据公式(5)则θ6可求.

求θ6时，带入对应的θ1θ5，不会产生新解。

求解θ234：

根据(1)第一行第三列与r13相等，则：

-s1ax + c1ay = c234s5

根据(1)第三行第三列与r33相等，则：

az = -s234s5

根据公式(5),可得θ234整体值。

注意，该值为计算理论值，但并非电机所转动的角度，即并不是示教器所显示的当前关节角。

求解θ2：

根据(1)第一行第四列与r14相等，则：

c1px + s1py = c234s5d6 - s234d5 + c23a3 + c2a2 (7)

根据(1)第三行第四列与r34相等，则：

pz - d1 = -s234s5d6 -c234d5 - s23a3 -s2a2 (8)

令

A = c234s5d6 - s234d5 + c23a3 + c2a2

B = -s234s5d6 -c234d5

C = c1px + s1py

D = pz - d1

则,(7) (8)化简为：

C = A + c23a3 + c2a2

D = B - s23a3 - s2a2

则：

c23a3 = C - A -c2a2

s23a3 = B - D -s2a2

令

M = C - A

N = B - D

则：

s23 = (N - s2a2)/a3 (9)

c23 = (M-c2a2)/a3 (10)

将上述等式化简整理，得

-(-2Na2)s2 + 2Ma2c2 = M*M + N*N + a2*a2 - a3*a3 (11)

再令：

E= -2Na2

F= 2Ma2

G = M*M + N*N + a2*a2 - a3*a3

则根据公式(4)，解得θ2.会有两种可能.故理论上2*2*2八组解。

根据(9)(10)与公式(5),得θ23值

则，根据θ234

θ4 = θ234 - θ23

θ3 = θ23 - θ2

不产生额外解。

部分验证程序如下：

//    Target <<  -0.687943   0.724766  0.0380584     214.3
//               0.725342    0.688386  0.00196604   -138.937
//              -0.0247739    0.0289579  -0.999274    200.473
//                      0          0          0          1;double px= 214.3;double py= -138.937;double pz= 200.473;double ax =  0.0380584;double ay = 0.00196604;double az = -0.999274;double ox = 0.724766;double oy = 0.688386;double nx = -0.687943;double ny = 0.725342;//get θ1//1 T01^-1//-s1*px + c1*py = c5*d6 + d2//c5 = -s1*ax + c1*ay//-(d6*ax + px)s1 + (py - d6*ay) = d2//-As1 + Bc1 = C//θ  =  atan2(B,A) - atan2(C, ±sqrt(A*A + B*B - C*C))double th1=0.0;double d1 = 98.50;double d2 = 121.50;double d5 = 102.50;double d6 = 94.0;double a2= 408.0;double a3= 376.0;double A = px - d6*ax;double B = py - d6*ay;double tmp1 = A*A + B*B - d2*d2;double tmp = sqrt(tmp1);//get θ1th1 = std::atan2(B,A) - std::atan2(d2, -tmp);std::cout << "joint1 ori: >>> " << ((th1)*ARC_TO_DEG) << std::endl;std::cout << "joint1 >>> " << ((th1 + M_PI)*ARC_TO_DEG) << std::endl;//get θ5double th5=0.0;tmp = -sin(th1)*ax + cos(th1)*ay;th5 = std::atan2(-sqrt(1-tmp*tmp), tmp);std::cout << "joint5 >>> " << (th5)*ARC_TO_DEG << std::endl;//get θ6double th6=0.0;th6 = std::atan2((-sin(th1)*ox + cos(th1)*oy)/sin(th5),(sin(th1)*nx - cos(th1)*ny)/sin(th5));std::cout << "joint6 >>> " << (th6)*ARC_TO_DEG << std::endl;//get θ2-θ3+θ4 ===============double th234=0.0;tmp = (cos(th1)*ax+sin(th1)*ay)/sin(th5);tmp1 = -(az/sin(th5));th234 = std::atan2(tmp1, tmp);  //-?std::cout << "joint234 sum : >>> " << (th234)*ARC_TO_DEG << std::endl;A =  cos(th234)*sin(th5)*d6 - sin(th234)*d5;B = -sin(th234)*sin(th5)*d6 - cos(th234)*d5;    // shao d6double C = cos(th1)*px + sin(th1)*py;double D = pz -d1;double M = C - A;double N = B - D;double E = -2*N*a2;double F = 2*M*a2;double G = M*M + N*N +a2*a2 -a3*a3;double th2 = 0.0;th2 = std::atan2(F,E) - std::atan2(G, sqrt(E*E+F*F-G*G));std::cout << "joint2 ori: >>> " << ((th2)*ARC_TO_DEG) << std::endl;std::cout << "joint2 >>> " << ((th2+M_PI/2)*ARC_TO_DEG) << std::endl;//    th2 = std::atan2(F,E) - std::atan2(G, -sqrt(E*E+F*F-G*G));
//    std::cout << "another joint2 ori: >>> " << ((th2)*ARC_TO_DEG) << std::endl;
//    std::cout << "another joint2 >>> " << ((th2-M_PI/2)*ARC_TO_DEG) << std::endl;double th2_3 = 0.0;th2_3 = std::atan2((N-sin(th2)*a2)/a3, (M-cos(th2)*a2)/a3);double th3 = 0.0;double th4 = 0.0;th3 = -(th2_3 -th2);th4 = th234 - th2_3 ;std::cout << "joint3 ori: >>>: >>> " << ((th3)*ARC_TO_DEG) << std::endl;std::cout << "joint4 ori:>>> " << ((th4)*ARC_TO_DEG) << std::endl;std::cout << "joint3 >>>: >>> " << ((th3+2*M_PI)*ARC_TO_DEG) << std::endl;std::cout << "joint4 >>> " << ((th4+M_PI/2)*ARC_TO_DEG) << std::endl;

关注公众公众号，后台留言“C++逆解验证”获取完整程序！