高斯消去法 | LU分解 | PA=LU分解（MatLab）-编程知识

一、问题描述

利用高斯消去法，LU 分解及PA=LU 分解求解非线性方程组。

二、实验目的

掌握高斯消去法、LU 分解、PA=LU 分解的算法原理；编写代码实现利用高斯消去法、LU 分解、PA=LU 分解来求解线性方程组。

三、实验内容及要求

1. 利用顺序高斯消去法求解如下方程组。

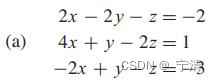
请添加图片描述

（注意将顺序高斯消去法封装为一个函数，函数名Gauss，该函数对应的文件同样命名为Gauss）。

function x = Gauss(A, b)n = length(b);for k = 1:n-1for i = k+1:nfactor = A(i,k) / A(k,k);A(i,k+1:n) = A(i,k+1:n) - factor * A(k,k+1:n);b(i) = b(i) - factor * b(k);endendx = zeros(n, 1);x(n) = b(n) / A(n,n);for i = n-1:-1:1x(i) = (b(i) - A(i,i+1:n) * x(i+1:n)) / A(i,i);end
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
b = [-2; 1; -3];
x = Gauss(A, b);
disp(x);

2. 对1 中的线性方程组，利用LU 分解进行求解，并输出L 和U。

（注意将本部分代码封装为一个函数，函数名LU，该函数对应的文件同样命名为LU）。

function [L, U] = LU(A)[n,~] = size(A);L = eye(n);U = A;for k = 1:n-1for i = k+1:nfactor = U(i,k) / U(k,k);L(i,k) = factor;U(i,k:n) = U(i,k:n) - factor * U(k,k:n);endend
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
[L, U] = LU(A);
disp(L);
disp(U);

3. 对1 中的线性方程组，利用PA=LU 分解进行求解，并输出P、L 和U。

（注意将本部分代码封装为一个函数，函数名PLU，该函数对应的文件同样命名为PLU）。

function [P, L, U] = PLU(A)[n,~] = size(A);P = eye(n);L = zeros(n);U = A;for k = 1:n-1[~, maxindex] = max(abs(U(k:n,k)));maxindex = maxindex + k - 1;U([k,maxindex],:) = U([maxindex,k],:);L([k,maxindex],1:k-1) = L([maxindex,k],1:k-1);P([k,maxindex],:) = P([maxindex,k],:);for i = k+1:nfactor = U(i,k) / U(k,k);L(i,k) = factor;U(i,k:n) = U(i,k:n) - factor * U(k,k:n);endendL = L + eye(n);
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
[P, L, U] = PLU(A);
disp(P);
disp(L);
disp(U);

四、算法原理

1. 给出高斯消去法、LU 分解、PA=LU 分解的算法原理

高斯消去法
高斯消去法是一种用于解线性方程组的算法，它的目标是将给定的系数矩阵转化为上三角矩阵（或更进一步转化为对角矩阵），这样可以直接使用回代法求解未知数。

步骤：
1. 选取主元（通常是当前列下的最大绝对值元素）。
2. 使用主元所在的行减去其他行，从而消去该列下主元以下的所有元素。
3. 对下一个列重复以上步骤，直到整个矩阵成为上三角形态。
4. 使用回代法求解未知数。
LU 分解
LU分解是将系数矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的过程。这样原方程组Ax=b变为LUx=b，先解Ly=b得到y，再解Ux=y得到x。

步骤：
1. 从第一行开始，将A的当前行元素存储在U的相应位置，将除对角线元素外的当前列元素存储在L的相应位置。
2. 使用L的当前列元素与U的当前行元素更新A的剩余部分。
3. 对于下一个列重复上述步骤。
PA=LU 分解
有时直接的LU分解不可能或者数值上不稳定，这时可以通过行交换获得稳定性。PA=LU分解将A分解为一个置换矩阵P、一个下三角矩阵L和一个上三角矩阵U。

步骤：
1. 选择一个主元并进行必要的行交换。
2. 按照LU分解的方法更新L和U的元素。
3. 对下一个列重复以上步骤。

2. 分别给出高斯消去法、LU 分解消去和回代过程的耗费的计算量。

高斯消去法
消去过程的计算量大约为(2/3)n^{3，而回代过程为n}2。所以总的计算量大约是O(n^3)。
LU 分解
LU分解的计算量和高斯消去法类似，主要来自于消去过程，大约为(2/3)n^{3。回代过程是O(n}2)，所以总的计算量仍然是O(n^3)。
PA=LU 分解
PA=LU分解的计算量和LU分解相似，因为增加的主要是行交换操作，这不会显著增加计算量。所以总的计算量仍然是O(n^3)。

五、测试数据及结果

给出算法输出的方程组的解。
给出算法输出的方程组的解及L 和U。
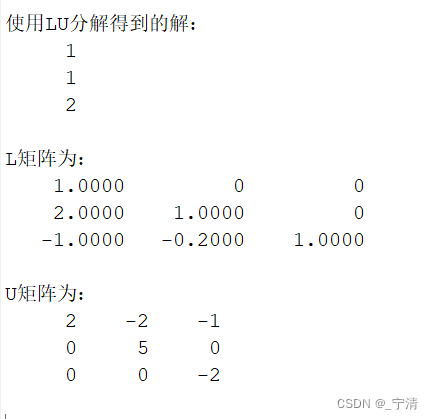
给出算法输出的方程组的解及P、L 和U。

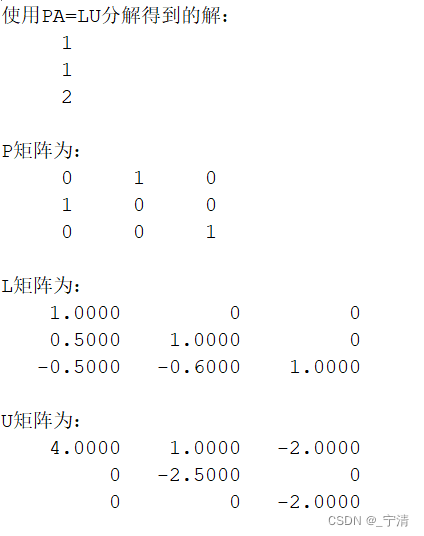
六、总结与思考

知识点的理解：

通过本次MATLAB实验，我深化了对线性代数中几个关键算法的理解：高斯消去法、LU分解和PA=LU分解。这些算法是解线性方程组的基石，并且在各种应用领域中都有广泛的使用。
代码实现的技巧：
- 使用MATLAB进行矩阵操作相对简单。例如，我们可以轻松地进行矩阵乘法、提取子矩阵和矩阵分解。
- 通过封装代码为函数，可以使整体代码结构更清晰、模块化，并增强代码的可读性和重用性。
- 适当的注释和文档对于理解和后期修改代码非常重要。

思考：

算法的应用：

虽然这三种算法在解决线性方程组方面很有用，但它们在处理大型矩阵或具有特定结构的矩阵时可能并不是最优的。例如，对于稀疏矩阵或对称正定矩阵，可能存在更高效的算法。考虑不同的问题背景和矩阵特点来选择合适的算法是很重要的。
数值稳定性：

实验中，我们简单地实现了上述算法，但在实际应用中，数值稳定性是一个需要考虑的重要问题。特别是在高斯消去法中，如果不适当地选择主元，可能会导致数值不稳定。这就是为什么PA=LU分解（带有行交换）在某些情况下更受欢迎。
优化与进一步学习：

MATLAB提供了一系列的内置函数和工具箱，例如lu函数，可以直接进行LU分解。通过比较我们自己的实现和MATLAB的内置函数，我们可以进一步了解性能和数值稳定性的问题，并从中学习。

综上，本次MATLAB实验不仅加深了我计算方法的理解，而且让我认识到在实际应用中考虑算法的数值稳定性和选择最适合的算法的重要性。