马尔可夫链(Markov Chain)是一种数学系统,它经过从一个状态到另一个状态的转换,这些转换遵循马尔可夫性质,即未来的状态只依赖于当前的状态,而与过去的状态(即如何到达当前状态)无关。这种性质称为无记忆性或马尔可夫性质。
定义: 马尔可夫链是指具有马尔可夫性质的随机过程。在离散时间情况下,它可以形式化为一个随机状态序列,每个状态都会依照一定的概率转移到另一个状态。
核心组成:
- 状态空间:系统可能存在的所有状态的集合。
- 转移矩阵:表示状态之间转移概率的矩阵,矩阵的元素 Pij 表示从状态 i 转移到状态 j 的概率。
- 初始状态分布:系统在时间开始时各状态的概率分布。
数学表示:

性质:
- 齐次马尔可夫链:如果转移概率不随时间变化,则称该马尔可夫链为齐次的。
- 稳态分布:如果存在一个概率分布,使得随着时间的推移,状态分布不再改变,那么这个分布称为稳态或平稳分布。
- 可逆链:如果一个马尔可夫链可以从其任何一个状态出发,经过一系列的转移概率回到原来的状态,则称这个链是可逆的。
- 吸收状态和瞬态状态:如果从某状态开始,马尔可夫链将停留在这个状态并不再离开,这样的状态被称为吸收状态;反之,如果可以离开,则称为瞬态状态。
用途:
- 预测系统的长期行为。
- 研究随机过程中的稳态行为。
- 在经济学、物理学、生物学等领域模拟各种随机系统。
- 计算机科学中的算法,比如随机游走、PageRank算法等。
举例: 一个简单的马尔可夫链例子是天气模型。假设只有晴天和雨天两种状态,转移矩阵如下:
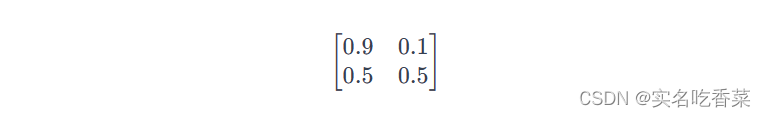
这个矩阵表示,如果今天是晴天,那么明天有 90% 的几率还是晴天,10% 的几率变成雨天;如果今天是雨天,明天有 50% 的几率是晴天,也有 50% 的几率仍然是雨天。
区别于其他随机过程: 马尔可夫链最核心的特点是它的无记忆性,这意味着过程的未来仅与当前状态有关,这与许多自然和人工过程的特点相符。这一特点使得马尔可夫链在计算上比那些需要知道整个历史的随机过程要简单得多。