文章目录
- 1 十二生肖
-
- 2 欢迎参加福建省大学生程序设计竞赛
-
- 3 匹配二元组的数量
-
- 4 元素交换
-
- 5 下棋的贝贝
-
- 6 方程
-
1 十二生肖
基本思路:
2 欢迎参加福建省大学生程序设计竞赛
基本思路:
- 一道排序的题,先按题数排序,题树相等时,按罚时排序
代码:
#include<bits/stdc++.h>
using namespace std;#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long
const int N = 1e6+10, INF=1e18+10;
struct Node{int x,y;
};
vector<Node> a;
bool cmp(Node xx,Node yy){if(xx.x!=yy.x)return xx.x>yy.x;return xx.y<yy.y;
}void solve(){int n; cin>>n;for(int i=1;i<=n;i++){int x,y; cin>>x>>y;a.push_back({x,y});}sort(a.begin(),a.end(),cmp);int num=0,prex=-1,prey=-1;for(auto i:a){if(i.x==prex&&i.y==prey) continue;num++;prex=i.x; prey=i.y;}cout<<num;
} signed main(){IOS;int T=1;
while(T--){solve();}return 0;
}
3 匹配二元组的数量
基本思路:
- 一对二元组(i,j)下标需要满足两个条件,一个是i<j,另一个是ai/j==aj/i. 对于第二个条件,我们不妨变一下形,得到aii == ajj.
- 每个数的值都乘以它的下标(下标从1开始),问题就变成了找到有多少个数相等,从这些数中任意选出两个组成一个匹配二元组,这不就是组合数吗,答案加上每个数个数的C(n,2),可以用哈希统计每个数有多少个!
代码:
#include<bits/stdc++.h>
using namespace std;#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long
const int N = 1e6+10, INF=1e18+10;
unordered_map<int,int> mp;
int n,ans;void solve(){cin>>n;vector<int> a(n+1);for(int i=1;i<=n;i++)cin>>a[i],mp[i*a[i]]++;for(auto i:mp)ans+=i.se*(i.se-1)/2;cout<<ans;} signed main(){IOS;int T=1;
while(T--){solve();}return 0;
}
4 元素交换
基本思路:
- 2*N的二进制数组,其中0、1的个数各占一半,要求交换任意两个元素,使得最后的数组不存在连续的0或1
- 我们可以发现最后数组只可能有两种状态:
- 一个状态是010101…01
- 另一个状态是101010…10
- 我们只需统计当前数组与目标数组(目标数组为以上两种状态中的一种)有多少个不同的元素,假设有x个不同的元素,那么x/2即为操作次数,为什么呢?因为每交换一次,就有两个元素回到正确的位置。
- 最后我们只需取两种情况中的最小值,即为最小操作次数!
代码:
#include<bits/stdc++.h>
using namespace std;#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long
const int N = 1e6+10, INF=1e18+10;
unordered_map<int,int> mp;
int ans=0;void solve(){int n;cin>>n;vector<int> a(2*n+1),b(2*n+1),c(2*n+1);for(int i=1;i<=2*n;i++){b[i]=0,c[i]=0;}for(int i=1;i<=2*n;i++)cin>>a[i];for(int i=1;i<=2*n;i++)if(i&1) b[i]=1;else c[i]=1;
int ans=INF,n1=0,n2=0;for(int i=1;i<=2*n;i++){if(a[i]!=b[i]) n1++;if(a[i]!=c[i]) n2++;}cout<<min(n1/2,n2/2);
} signed main(){IOS;int T=1;
while(T--){solve();}return 0;
}
5 下棋的贝贝
基本思路:
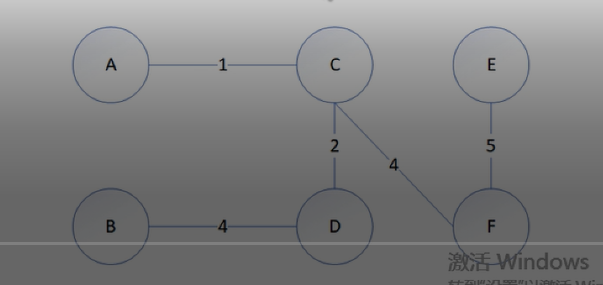
- 首先我们需要理解题意,两个点坐标的曼哈顿距离等于1,这两点就是邻居!求出所有棋子邻居数量总和的最大值是多少?
- 画图的可能会更直观些

- 有图可以发现,我们更倾向于构造正方形,这样能才能保证邻居数量总和最大
- 每个棋子的最多的邻居是4个,即上下左右都是邻居。还可以发现处于边界位置的方块可能有一个邻居,两个邻居或者三个邻居。
- 我们不妨假设每个棋子都有4个邻居,那么所有棋子邻居数量总和就为4n,然后在减去每个棋子多出来的邻居,由图不难发现,只有处于边界的棋子的邻居数量是少于4的。
- 我们知道如果是完整的矩形,位于矩形四个角的棋子会有2个邻居,其余处于边界的棋子都有3个邻居。我们可以把缺的部分补成一个矩形!那么多出来的邻居总数=矩形的长2+矩形的宽2。结合示意图模拟一下不难发现补出来的的棋子不会对多出的邻居总数产生影响。
代码:
void solve(){int n; cin>>n;int l,h,m;m=sqrt(n);l=h=m;if(l*h<n) l++;if(l*h<n) h++;cout<<4*n-2*l-2*h;
}
6 方程
思路:
- 我们直到了x+1/x = k, 求 x^(n) + 1/(x^n)
- 我们不妨设f(n)= x^(n) + 1/(x^n) 是关于x的函数
- 以下我粗糙的证明了一下递推公式:

- 我们虽然找到了递推公式,但是发现n,k的范围都是1e9,直接一项一项求的话肯定会超时的!这时我们就需要矩阵快速幂来优化!f(1)=k , f(2)=k*k-2; 构建矩阵第一行:(0,-1) 第二行(1,k)推得f(2),f(3)
代码:
#include<bits/stdc++.h>
using namespace std;#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long
const int N = 2e2+10, p=1e9+7;
int n=2,f[N+1],a[N+1][N+1];void aa(){long long w[N+1][N+1];memset(w,0,sizeof(w));for(int i=1;i<=n;i++)for(int k=1;k<=n;k++)if(a[i][k])for(int j=1;j<=n;j++)if(a[k][j])w[i][j]+=a[i][k]*a[k][j],w[i][j]%=p;memcpy(a,w,sizeof(a));
}void fa(){int w[N+1];memset(w,0,sizeof(w));for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)w[i]+=f[j]*a[j][i],w[i]%=p;memcpy(f,w,sizeof(f));
}void matrixpow(int k){while(k){if(k&1) fa();aa();k>>=1;}
}void solve(){int m,k;cin>>m>>k;f[1]=k,f[2]=((k*k-2)%p+p)%p;a[1][1]=0,a[1][2]=-1;a[2][1]=1,a[2][2]=k;matrixpow(m-1);cout<<f[1]<<endl;
} signed main(){
int T=1;cin>>T;while(T--){solve();}return 0;
}