491. 非递减子序列
中等
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况
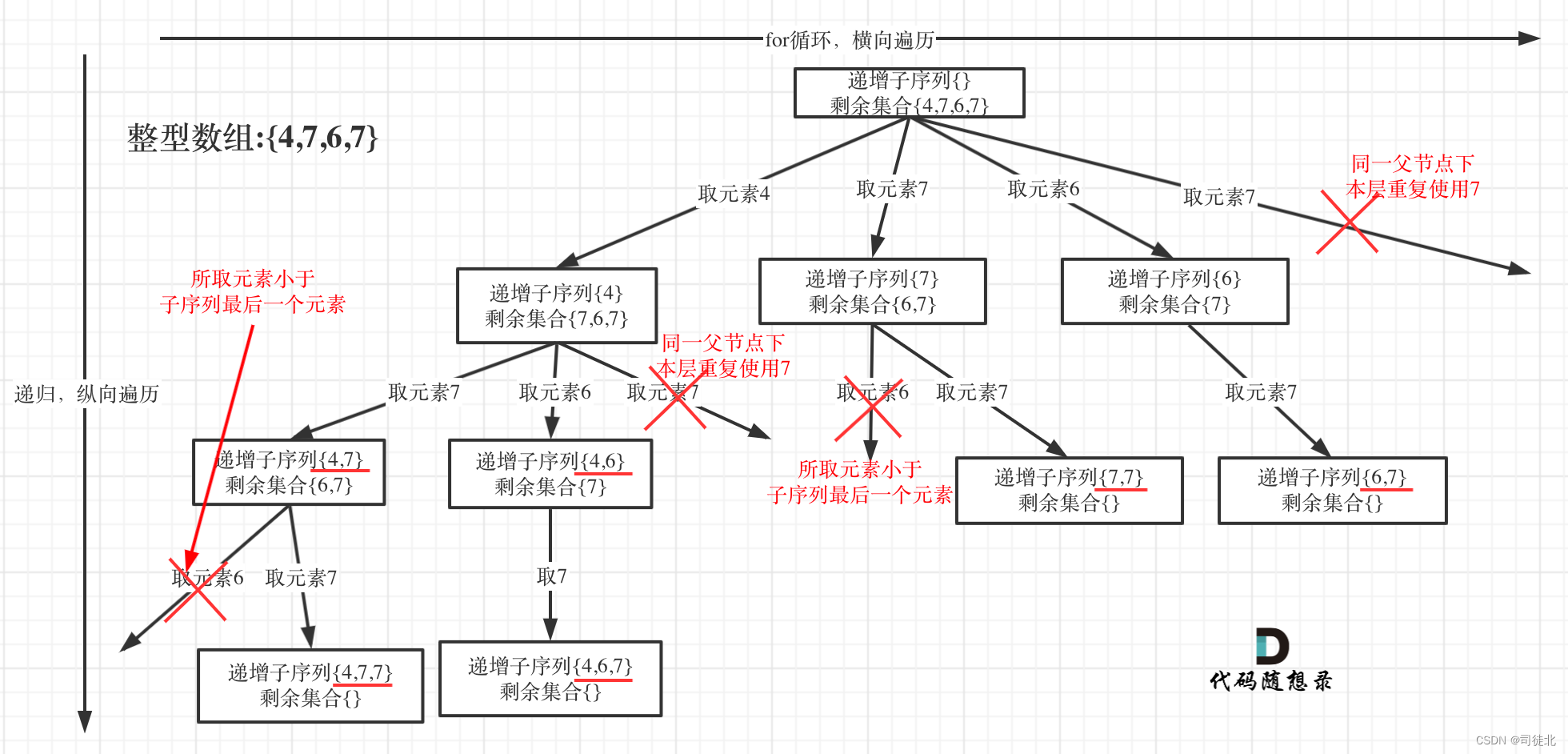
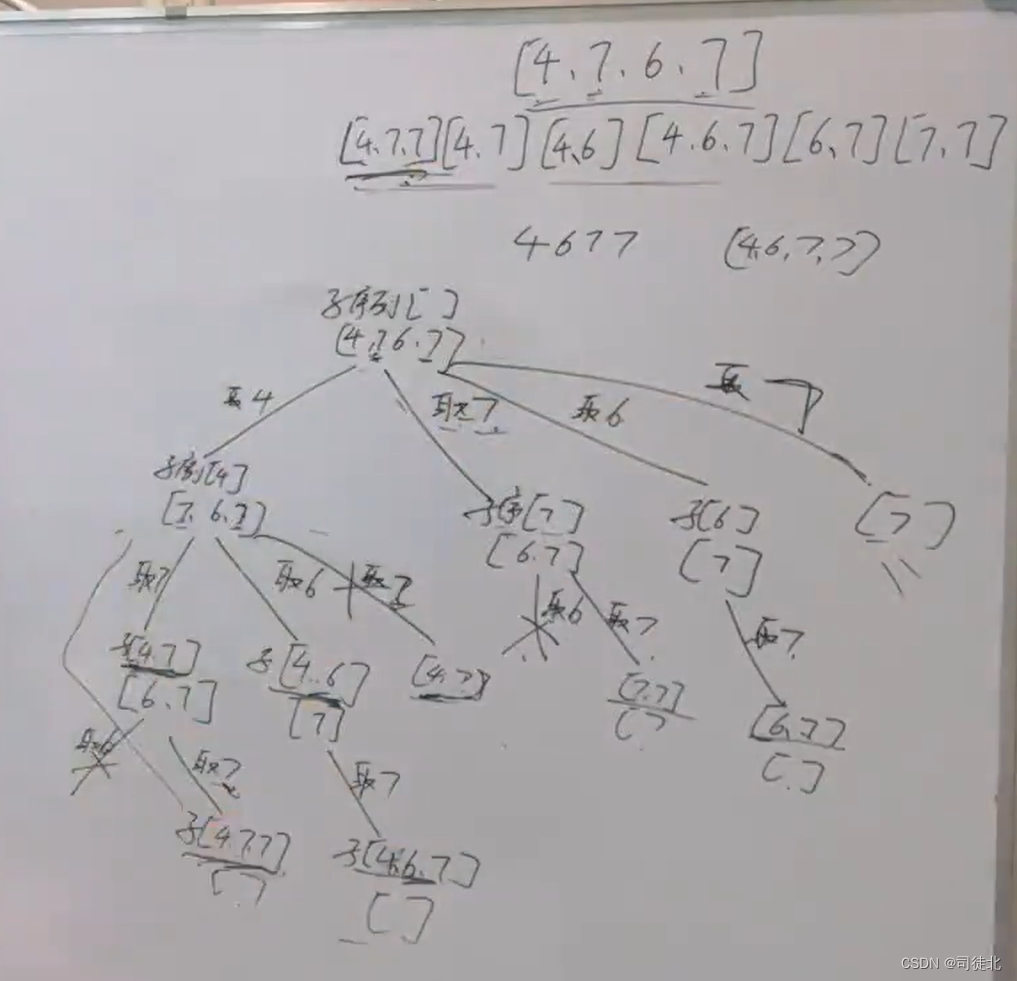
class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backtrack(nums, 0);return res;}public void backtrack(int nums[], int start) {if (path.size() >= 2) {res.add(new ArrayList<>(path));}// 借助 set 对 [idx + 1, nums.length - 1] 范围内的数去重Set<Integer> set = new HashSet<>(); //每个循环里都会有一个这个哈希表,不用担心别的分支层的哈希表影响到这个地方的哈希表for (int i = start; i < nums.length; i++) {if (!path.isEmpty() && nums[i] < path.get(path.size() - 1)) {continue; // 如果这个数比上个数小,那就不是递增了}if (set.contains(nums[i])) {continue; // 如果这一层已经用过这个数了,那就砍掉这个分支}set.add(nums[i]);path.add(nums[i]);backtrack(nums, i + 1);path.remove(path.size() - 1);}}
}
46. 全排列
中等
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案
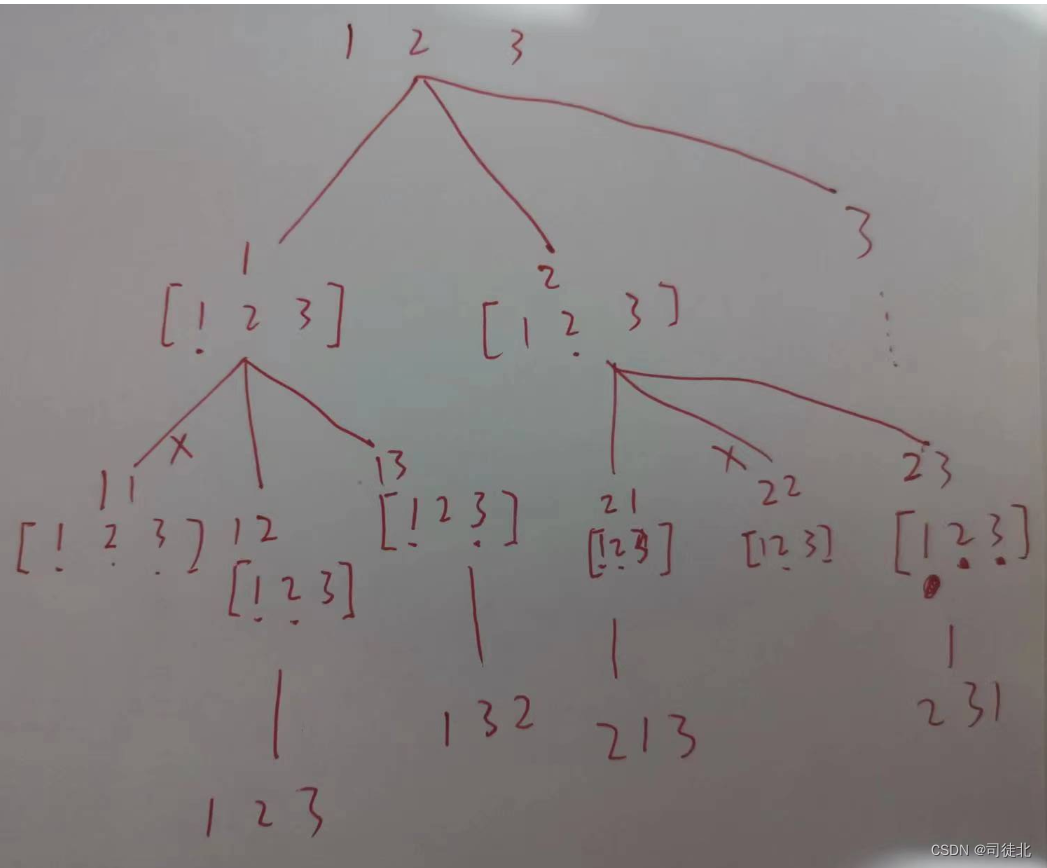
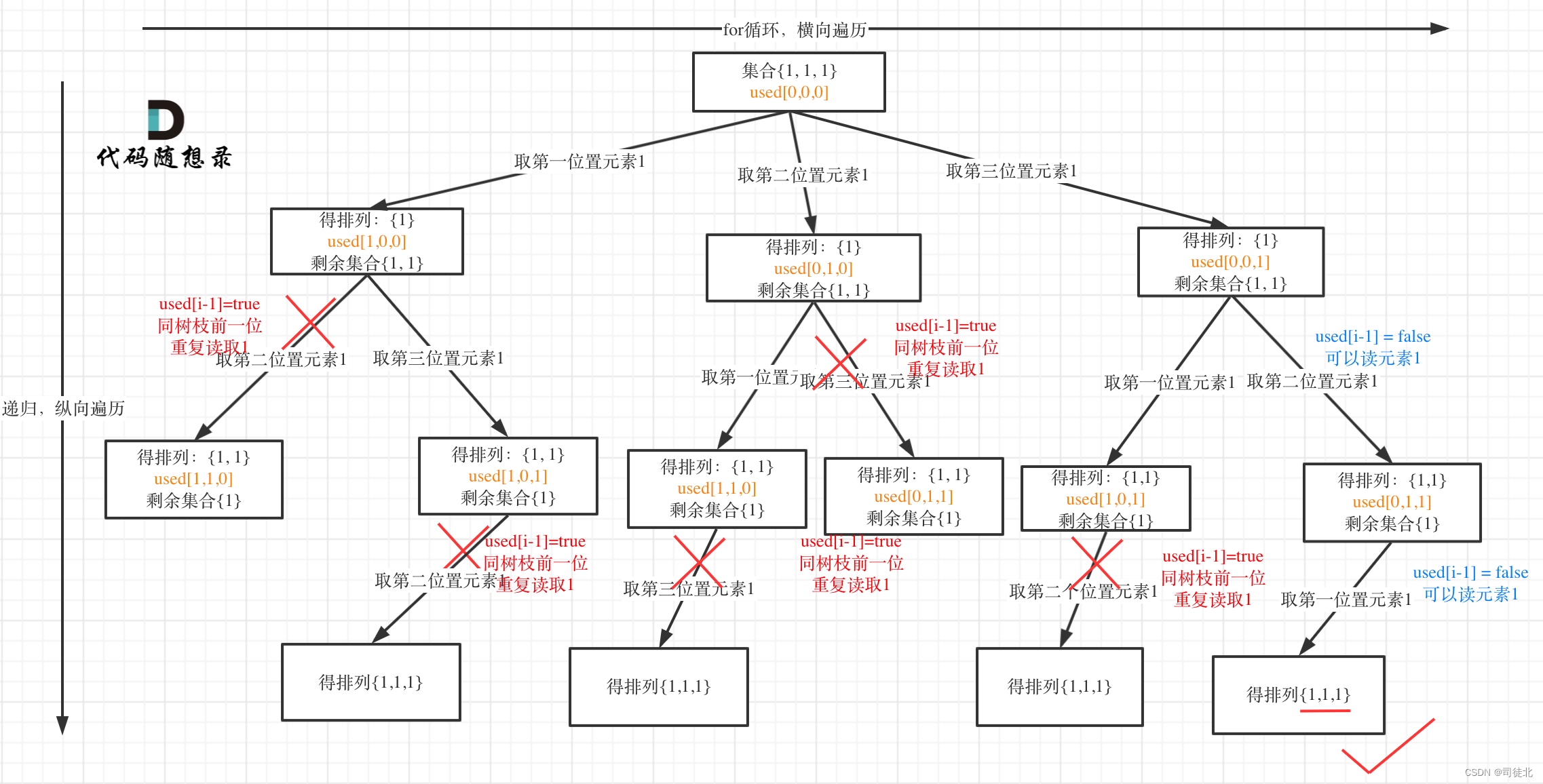
难点:每次都会延伸出nums.length个分支,只不过都被砍了(见上图),整个算法复杂度很高,所以提示:1 <= nums.length <= 6
class Solution {List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> permute(int[] nums) {backtrack(nums);return res;}public void backtrack(int[] nums) {if (path.size() == nums.length) {res.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {if (path.contains(nums[i])) {continue;}path.add(nums[i]);backtrack(nums);path.remove(path.size() - 1);}}
}
47. 全排列 II
中等
相关标签
相关企业
给定一个可包含重复数字的序列 ,按任意顺序 返回所有不重复的全排列。
class Solution {List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();boolean[] used;public List<List<Integer>> permuteUnique(int[] nums) {used = new boolean[nums.length];Arrays.fill(used, false); // 全部填充为falseArrays.sort(nums);backtrack(nums);return res;}public void backtrack(int[] nums) {if (path.size() == nums.length) {res.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue; // used[i - 1] == false做得是树层上的去重,因为,当前数等于前一个数,而且前一个数标记为false,说明它已经被使用过了,如果它是true,说明在它的这个树枝里} // used[i - 1] == true 做得是树枝上的去重if (used[i] == false) {path.add(nums[i]);used[i] = true;backtrack(nums);path.remove(path.size() - 1);used[i] = false;}}}
}
难点:这个题,有树枝去重和树层去重两种方式,可以仔细思考,推荐树层去重,更高效
树层去重:used[i - 1] == false
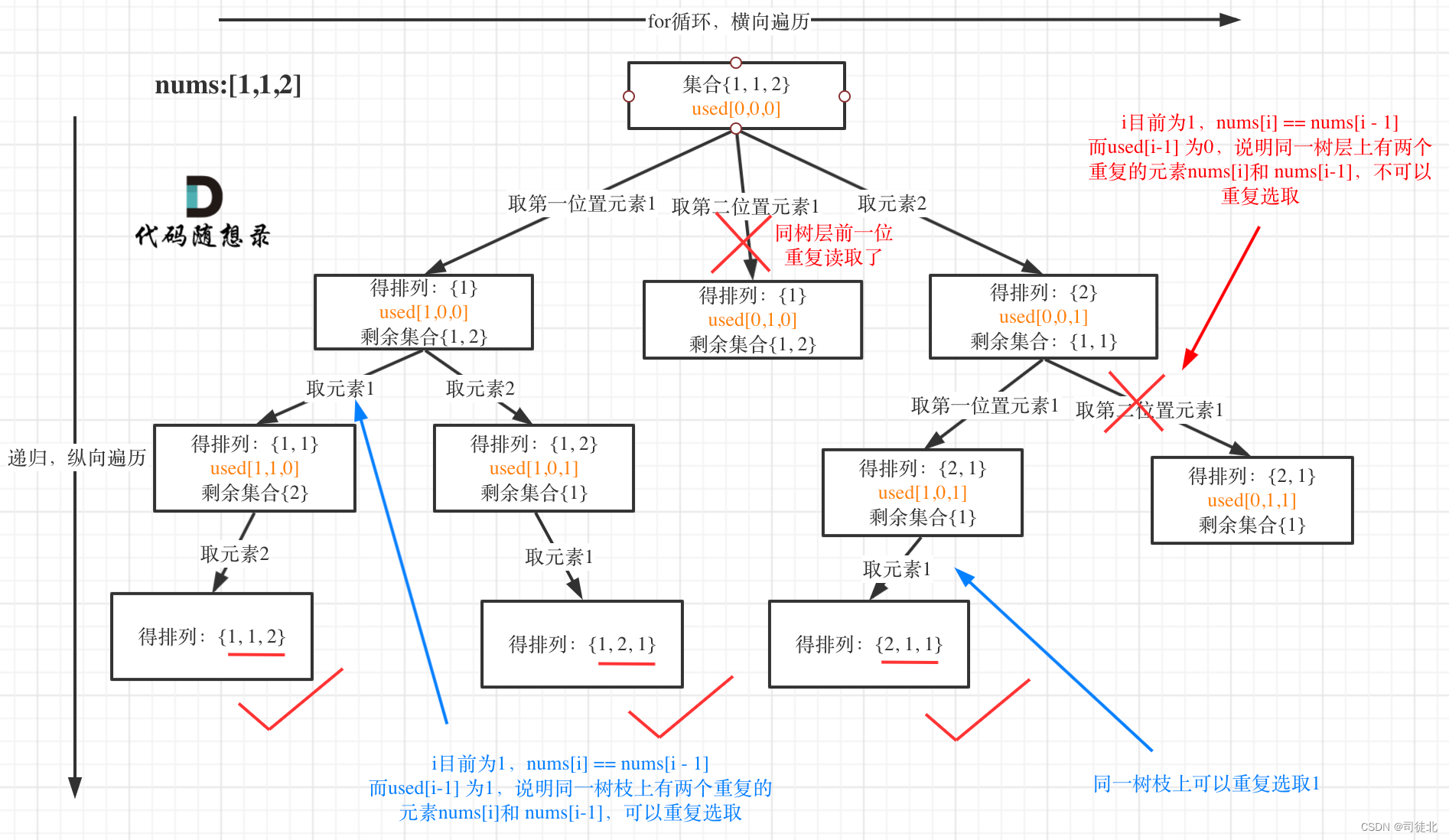
树枝去重:used[i - 1] == true