首先，我们要理解为什么要对“光谱数据进行特征波长优选”以及这是在干嘛，光谱数据可以想象成一长串的彩色条纹，每种颜色对应一个波长，就像彩虹一样。这些颜色的条纹代表了从某种物质（比如植物、矿石或是食品）反射或透过光的特性。通过分析这些条纹，我们可以了解物质的很多信息，比如它是什么成分、有没有污染、熟度等等。

        但问题在于这长串的条纹实在太长了，里面有很多颜色，有的重要有的不重要。如果把每种颜色都当成一个线索来追，工作量会非常巨大，而且有很多无用功。所以我们需要找出那些最关键的颜色（也就是波长），这样我们就可以只关注这些颜色，提高我们的寻宝效率。

        特征波长优选，就是通过一系列数学方法和技巧，来确定哪些颜色的条纹（波长）最能帮助我们了解我们想要知道的信息。确定了这些关键的颜色条纹之后，我们在分析物质时就可以只看这些颜色，这样既省时又准确。

一、主成分分析法(Principal Component Analysis,PCA)

(1)原理详解

        假想你正在用一台相机从不同角度拍摄一座山。每张照片都提供了山的视角，但所有的照片都有重复的信息（都是同一座山），同时每个角度也显示了一些独特的细节。PCA的目标就是找出最好的几个角度，以最简洁的方式展现出山的最关键特征。

在数学上，PCA是这样实现的：

1. 数据中心化： 首先，要将每个特征（如，每张照片的视角）调整为以零为中心，也就是说，我们需要从每个特征中减去它的平均值。这样做的目的是让PCA后续的计算更加方便，同时去除数据位置的影响，只保留数据形状的信息。

2. 计算协方差矩阵： 接下来，我们计算数据的协方差矩阵。在我们的比喻中，协方差矩阵描述了不同角度之间如何变化，或者说这些角度是否会同时增加或减少。如果两个角度通常同时增减，它们就具有高协方差，意味着这两个角度信息重合得很多。

3. 找出主成分： 现在，我们要找出主成分，也就是找到那些能够捕捉最多山的特征的“最好的角度”。数学上，这意味着我们要找到协方差矩阵的特征向量，并将它们按照对应特征值的大小排序。特征值越大，对应的特征向量就能捕捉越多的信息（变异性）。

4. 降维： 最后，我们选择前几个最大的特征值和对应的特征向量。这些特征向量称为“主成分”，它们定义了新的坐标系，这个坐标系的坐标轴指向数据变化最大的方向。通过将原始数据投影到这些主成分上，我们可以用更少的维度来描述数据，同时保留最重要的信息。

        简而言之，PCA就像是找到了描述山的几张最有代表性的照片。每张照片（主成分）都尽可能多地包含了山的信息，且每张照片都提供了之前照片中没有的信息。通过这几张照片，我们可以用最少的数据捕捉到最关键的特征。

1)生成模拟光谱数据

def generate_spectral_data(samples, features):np.random.seed(0)return np.random.rand(samples, features)

• generate_spectral_data 函数使用np.random.rand创建一个给定形状（samples行，features列）的数组，数组中的每个元素都是在[0,1)区间内均匀分布的随机浮点数。
• 设置随机种子（np.random.seed(0)）保证每次运行代码时生成的随机数是相同的，这有助于结果的可重复性。

2)PCA算法实现

def apply_pca(data, n_components):pca = PCA(n_components=n_components)principal_components = pca.fit_transform(data)return principal_components, pca.explained_variance_ratio_

• apply_pca 函数利用scikit-learn中的PCA类来对输入数据data执行主成分分析。
• n_components参数指定了PCA降维后保留的主成分数目。
• fit_transform方法计算PCA并将数据转化为主成分空间，返回转换后的数据。
• explained_variance_ratio_属性表示每个主成分解释的方差比例。

(2)完整代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA# 生成模拟光谱数据
def generate_spectral_data(samples, features):np.random.seed(0)return np.random.rand(samples, features)# 使用PCA进行特征提取
def apply_pca(data, n_components):pca = PCA(n_components=n_components)principal_components = pca.fit_transform(data)return principal_components, pca.explained_variance_ratio_# 主函数
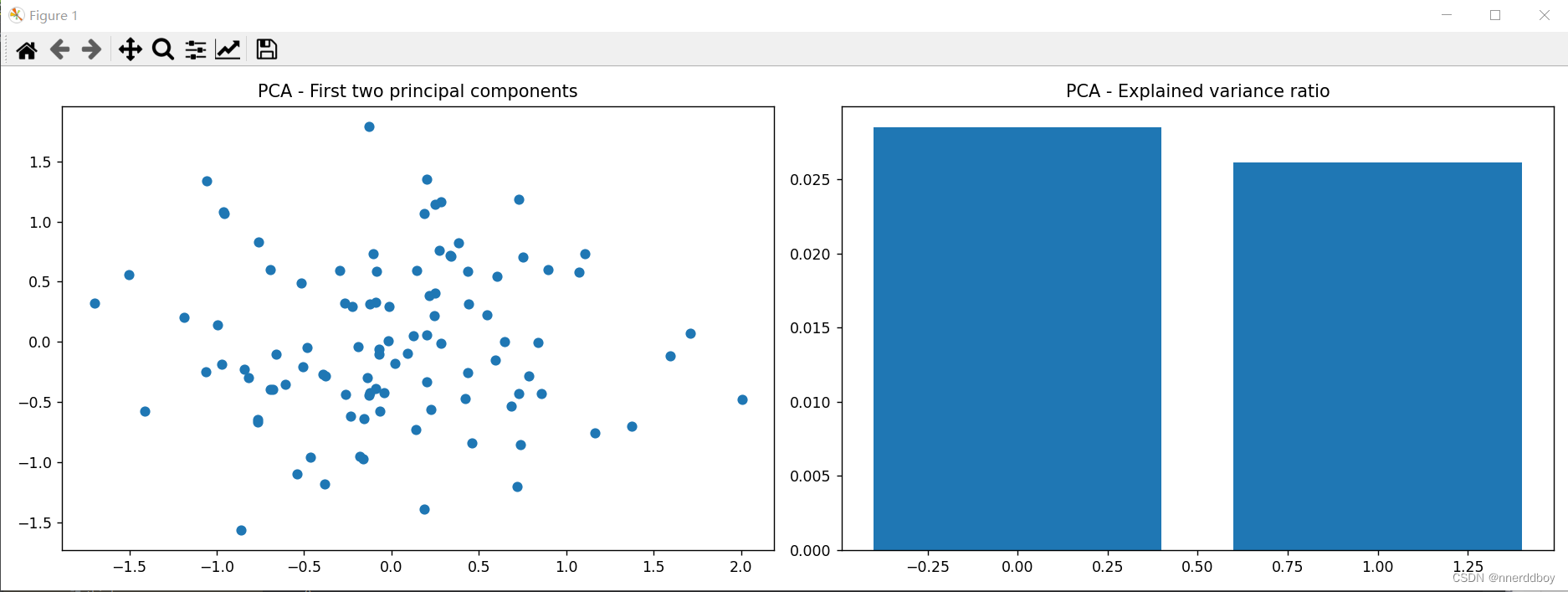
def main():# 模拟生成光谱数据，设定样本数和特征数samples = 100  # 样本数features = 200  # 特征数，即波长数spectral_data = generate_spectral_data(samples, features)# 应用PCA提取特征principal_components, explained_variance_ratio = apply_pca(spectral_data, n_components=2)# 绘制模拟光谱数据的前两个主成分plt.figure(figsize=(15, 5))plt.subplot(1, 2, 1)plt.scatter(principal_components[:, 0], principal_components[:, 1])plt.title("PCA - First two principal components")# 绘制解释方差比例plt.subplot(1, 2, 2)plt.bar(range(len(explained_variance_ratio)), explained_variance_ratio)plt.title("PCA - Explained variance ratio")plt.tight_layout()plt.show()if __name__ == "__main__":main()

(3)运行结果

二、协同区间偏最小二乘法（SiPLS）

(1)原理详解

        假设你是一名音乐制作人，你有一段复杂的音轨，里面包含了各种乐器的音频信号。你的目标是找出音轨中那些对整体音乐风格贡献最大的乐器组合。你不可能一次性听清每个乐器的影响，因此你需要一种方法来区分和评估每种乐器的重要性。

SiPLS的做法类似于这样一个过程：

1. 划分区间： 就像你可能会把音轨分成多个部分来单独分析每个乐器一样，SiPLS首先将整个数据集（例如光谱数据）分成多个小的区间。这样做的目的是因为不同区间的数据（或者音乐中的乐器组合）可能会有不同的重要性。

2. 区间选择： 接着，对于每个区间，SiPLS评估它们对于输出结果（可能是化学成分的浓度或者音乐风格的贡献）的影响。这个步骤类似于你听每个乐器段落并判断它对整体作品的贡献大小。

3. 组合和构建模型： 根据这些区间的贡献，SiPLS会选择那些贡献最大的区间并将它们组合起来。这就像是你选取那些最能代表音乐风格的乐器组合，并将它们混合以形成一个完整的音轨。

4. 优化和评估： 最后，SiPLS通过对这些选定区间的数据进行偏最小二乘回归分析来构建一个预测模型。在音乐制作中，你会尝试调整不同乐器的音量和效果来使整体作品听起来最好。同样，SiPLS调整模型参数来确保预测结果与实际结果尽可能接近。

总的来说，SiPLS的目的是在大量复杂数据中找到最有信息量的部分，然后只用这些部分来构建一个有效的模型。在光谱分析中，这意味着可以更准确地预测样本的性质，同时减少了计算量和噪声的影响。

1)生成模拟光谱数据

def generate_spectral_data(samples, features, noise_level=0.1):np.random.seed(0)# 生成波长wavelengths = np.linspace(400, 2500, features)# 生成光谱数据，基于某些波长的线性组合加噪声X = np.random.randn(samples, features) + np.sin(wavelengths) * 10# 生成响应变量，同样是波长的线性组合加噪声Y = np.dot(X, np.sin(wavelengths)) * 0.5 + np.random.randn(samples) * noise_levelreturn X, Y, wavelengths

• samples：数据集中的样本数量。
• features：每个样本的特征数量，也可以看作是波长数。
• noise_level：添加到数据中的噪声水平，用于更接近真实世界的情况。
• X：模拟光谱数据矩阵。
• Y：目标变量，通常是样本的某些特性，它与光谱数据有关联。
• wavelengths：对应于光谱数据特征的波长值。

2)SiPLS算法实现

def SiPLS(X, Y, wavelengths, interval_length=10):n_intervals = X.shape[1] // interval_lengthscores = []for i in range(n_intervals):start = i * interval_lengthend = start + interval_lengthpls = PLSRegression(n_components=2)score = -np.mean(cross_val_score(pls, X[:, start:end], Y, cv=5, scoring='neg_mean_squared_error'))scores.append(score)# 返回每个区间的性能评分return np.array(scores), wavelengths[:n_intervals*interval_length:interval_length]

• interval_length：决定了划分子区间的长度。
• n_intervals：根据给定的光谱特征数和区间长度计算总共可以划分的区间数。
• scores：记录每个区间PLS模型的均方误差（MSE）分数列表。
• 循环遍历每个区间，对每个子区间执行PLS回归，并通过交叉验证计算MSE分数。
• 返回每个区间的MSE分数和对应的波长值。

(2)完整代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSRegression
from sklearn.model_selection import cross_val_score# 生成模拟光谱数据
def generate_spectral_data(samples, features, noise_level=0.1):np.random.seed(0)# 生成波长wavelengths = np.linspace(400, 2500, features)# 生成光谱数据，基于某些波长的线性组合加噪声X = np.random.randn(samples, features) + np.sin(wavelengths) * 10# 生成响应变量，同样是波长的线性组合加噪声Y = np.dot(X, np.sin(wavelengths)) * 0.5 + np.random.randn(samples) * noise_levelreturn X, Y, wavelengths# SiPLS算法
def SiPLS(X, Y, wavelengths, interval_length=10):n_intervals = X.shape[1] // interval_lengthscores = []for i in range(n_intervals):start = i * interval_lengthend = start + interval_lengthpls = PLSRegression(n_components=2)score = -np.mean(cross_val_score(pls, X[:, start:end], Y, cv=5, scoring='neg_mean_squared_error'))scores.append(score)# 返回每个区间的性能评分return np.array(scores), wavelengths[:n_intervals*interval_length:interval_length]# 主函数
def main():samples = 100features = 200X, Y, wavelengths = generate_spectral_data(samples, features)# 应用SiPLSscores, selected_wavelengths = SiPLS(X, Y, wavelengths)# 绘图展示原始数据plt.figure(figsize=(15, 6))plt.subplot(2, 1, 1)plt.plot(wavelengths, X.T, color='grey', alpha=0.5)plt.title("Simulated Spectral Data")# 绘图展示SiPLS区间评分plt.subplot(2, 1, 2)plt.plot(selected_wavelengths, scores, marker='o')plt.xlabel('Wavelength (nm)')plt.ylabel('MSE Score')plt.title('SiPLS Interval Scores')plt.tight_layout()plt.show()if __name__ == "__main__":main()

(3)运行结果

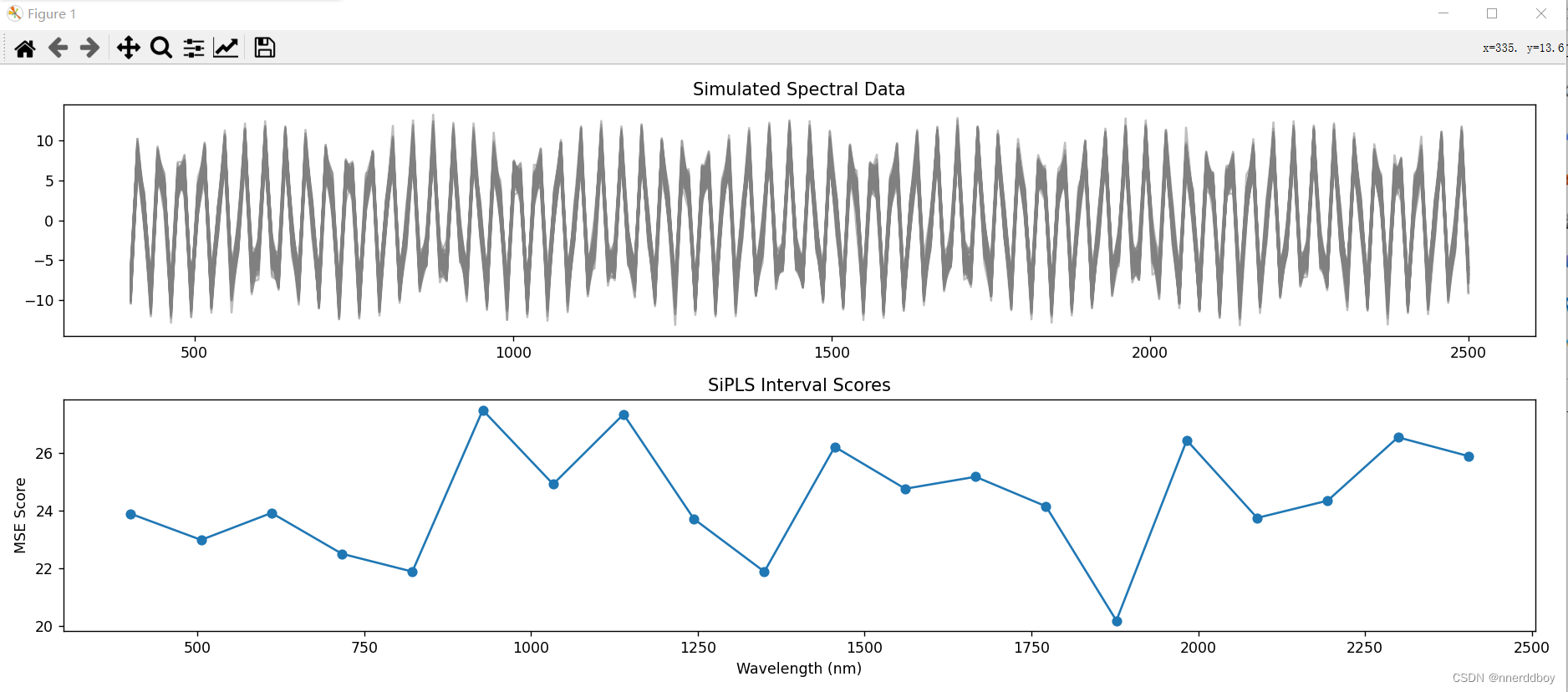
        由图可通过对比不同子区间的MSE分数，来选择最佳特征波长进行后续分析。

三、连续投影算法（Successive Projections Algorithm,SPA）

(1)原理详解

        想象一下，你有一个乐队，每个乐器都发出不同的声音。如果要为一首曲子选择最合适的乐器组合，你会尝试找出哪些乐器最能代表歌曲的核心旋律和节奏，同时确保它们听起来不会混在一起，即每个乐器的声音都是清晰和独特的。

SPA的工作原理即为以下几个步骤：

1. 开始时，所有乐器都可选择： SPA开始时，所有的变量（在光谱数据中即为所有波长）都是可选择的。在乐队的比喻中，这就像是所有乐器都准备好了，等待被选中加入曲目。

2. 选择第一个乐器： 首先，SPA会从所有乐器中选择一个最能代表曲目的乐器。在数学上，这相当于从所有变量中选择一个与响应变量（可能是化学成分的浓度）关联最紧密的变量。

3. 寻找与已选乐器不同的乐器： 接下来，SPA会在剩下的乐器中寻找一个与已选乐器尽可能不同的乐器。数学上，这意味着寻找一个与已选变量正交（或者说相关性最小）的变量。这样可以确保新选择的变量能提供一些新信息，而不是重复之前已选择的变量的信息。

4. 迭代选择： SPA会重复上述过程，每次都选出一个与当前已选集合正交的新变量。这就像是一个个挑选乐器，确保每个新增的乐器都能带来不同的音色，从而丰富整首歌曲。

5. 终止条件： 这个过程会一直进行，直到达到预先设定的乐器数量（或者在光谱数据分析中的变量数量）或者进一步添加乐器（变量）不再使得曲目（模型）有显著提升。

        通过SPA，你最终会得到一个由互相独立的乐器（变量）组成的乐队（数据子集），它们合在一起能够很好地演奏出一首曲子（构建一个有效的预测模型）而不会有太多的噪音（不必要的信息或多余的变量）干扰听众（模型的性能）。

        所以，SPA帮助你从大量的可能选项中挑选出最有代表性且互不干扰的一小部分，用以构建一个既简洁又有效的模型。

SPA算法的实现

def successive_projections_algorithm(X, num_variables):num_samples, num_features = X.shapeselected_variables = []P = np.eye(num_samples)for i in range(num_variables):var_projections = np.dot(X.T, P).Tvar_norms = np.sum(var_projections**2, axis=0)next_var = np.argmax(var_norms)selected_variables.append(next_var)xi = X[:, [next_var]]P = P - np.dot(np.dot(P, xi), np.dot(xi.T, P)) / np.dot(np.dot(xi.T, P), xi)return selected_variables

• 函数successive_projections_algorithm(X, num_variables)接受输入数据X（假设为光谱数据）和一个整数num_variables，表示要选择的变量数量。
• 算法初始化一个单位矩阵P作为投影矩阵。
• 在每次迭代中：
  • 计算当前残差矩阵X和P的乘积，得到各变量的投影。
  • 计算每个变量投影的范数（即投影向量的平方和），选择范数最大的变量，因为它包含最多的残差信息。
  • 更新所选变量的索引列表selected_variables。
  • 使用更新后的投影矩阵P计算新的残差矩阵。
  • 最后返回选择的变量索引列表。

(2)完整代码

import numpy as np
import matplotlib.pyplot as pltdef successive_projections_algorithm(X, num_variables):num_samples, num_features = X.shapeselected_variables = []P = np.eye(num_samples)for i in range(num_variables):var_projections = np.dot(X.T, P).Tvar_norms = np.sum(var_projections**2, axis=0)next_var = np.argmax(var_norms)selected_variables.append(next_var)xi = X[:, [next_var]]P = P - np.dot(np.dot(P, xi), np.dot(xi.T, P)) / np.dot(np.dot(xi.T, P), xi)return selected_variables# 模拟一些数据作为示例
np.random.seed(0)
num_samples = 200
num_features = 100
X = np.random.rand(num_samples, num_features)  # 模拟的光谱数据# 使用SPA选择特征
num_selected_variables = 10  # 你希望选择的特征数量
selected_wavelengths = successive_projections_algorithm(X, num_selected_variables)# 绘图以显示原始光谱数据和选定的特征波长
average_spectrum = np.mean(X, axis=0)
wavelengths = np.arange(num_features)  # 假设波长是连续的整数值plt.figure(figsize=(12, 6))
plt.plot(wavelengths, average_spectrum, label='Average Spectrum')
plt.scatter(wavelengths[selected_wavelengths], average_spectrum[selected_wavelengths], color='red', label='Selected Wavelengths')
plt.xlabel('Wavelength')
plt.ylabel('Intensity')
plt.title('Spectral Data with Selected Features by SPA')
plt.legend()
plt.show()

(3)运行结果

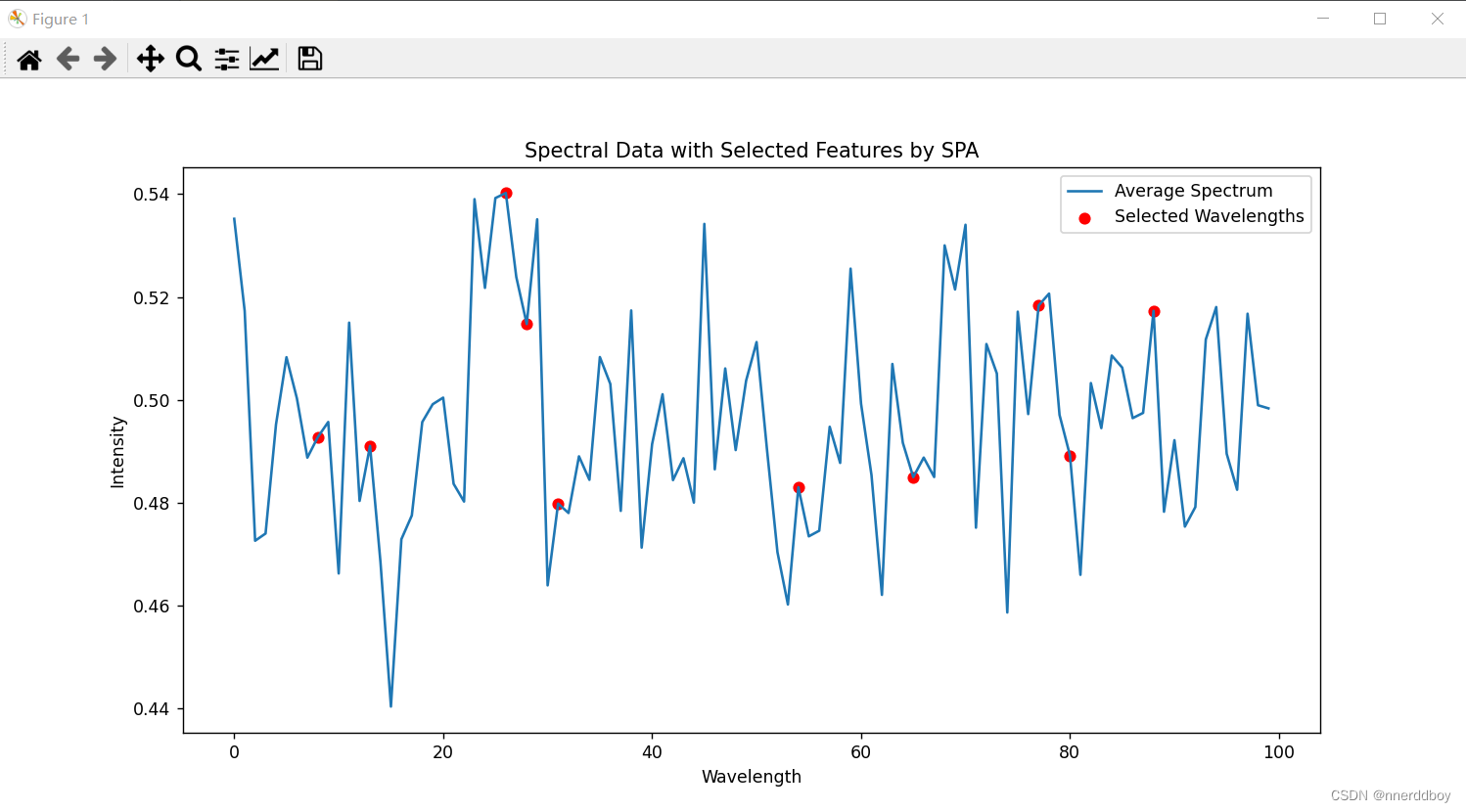
四、竞争自适应重采样算法（Competive Adaptive Reweighted Sampling ,CARS）

(1)原理详解

        想象一下，你是一个厨师，面前放着各种各样的食材。你的任务是从中选择出最合适的几种来制作一道美味的菜肴。但是，有一个挑战：你的菜板空间有限，不能同时准备太多的食材。

        这里是你的策略：

1. 先试一小部分：你首先随机挑一小撮食材做个样品菜，看看效果怎样。

2. 评估每种食材：根据样品菜的口感，你评估每种食材的贡献大小，哪些食材让菜更美味，哪些没有太大帮助。

3. 淘汰一些食材：你决定淘汰掉那些看起来不怎么影响味道的食材，因为你的空间有限，需要给更有潜力的食材留下位置。

4. 调整食材比重：根据你对每种食材的评估，你决定调整它们在菜中的比重，比如增加某些食材的用量，减少或淘汰另一些。

5. 重复过程：你不断重复这一过程，每次用不同的食材组合做样品菜，评估，淘汰，直到找到那个完美的配方，即最能提升你菜品口味的食材组合。

6. 最终结果：最后，你得到了一个既不过多也不过少，每种食材都能发挥其最佳效果的食材组合，这就是你的拿手好菜。

        将这个比喻转换为 CARS 算法的话，这些食材就像是你要分析的数据中的特征（如光谱数据中的波长），而美味的菜肴就像是一个强大的预测模型，你希望只用最有信息量的特征来做出预测。CARS 通过一个迭代的过程，不断地选择和调整特征，以确保最终模型的精确度和可解释性。就像厨师通过尝试和调整来找到最好的食材组合一样。

利用 SelectKBest 进行特征选择

selector = SelectKBest(score_func=f_regression, k=10)
X_selected = selector.fit_transform(X, y)

创建一个SelectKBest对象，用于特征选择。score_func参数设置为f_regression，这意味着选择特征的依据是每个特征对目标变量的 F-统计量。参数k=10指定我们希望选择的特征数量。

fit_transform方法将选择操作应用于数据X和目标y，结果是筛选后的数据X_selected，它只包含了我们希望保留的那些最佳特征。

(2)完整代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_selection import SelectKBest, f_regression# 假设 X 是模拟的光谱数据，y 是相应模拟的目标变量
np.random.seed(0)
X = np.random.rand(100, 200)  # 100个样本，200个波长点
y = np.random.rand(100)       # 100个样本的目标值# 使用 SelectKBest 进行特征选择，这里使用的是 f_regression 方法
# f_regression 是用于回归任务的特征选择函数，它不是CARS算法
selector = SelectKBest(score_func=f_regression, k=10)
X_selected = selector.fit_transform(X, y)# 绘制原始数据和经过特征选择后的数据
plt.figure(figsize=(14, 6))# 绘制原始数据
plt.subplot(1, 2, 1)
plt.imshow(X.T, aspect='auto')
plt.colorbar()
plt.title('Original Spectra Data')# 绘制特征选择后的数据
plt.subplot(1, 2, 2)
selected_features = selector.get_support(indices=True)
selected_spectra = X[:, selected_features]
plt.imshow(selected_spectra.T, aspect='auto')
plt.colorbar()
plt.title('Selected Features')plt.show()

(3)运行结果

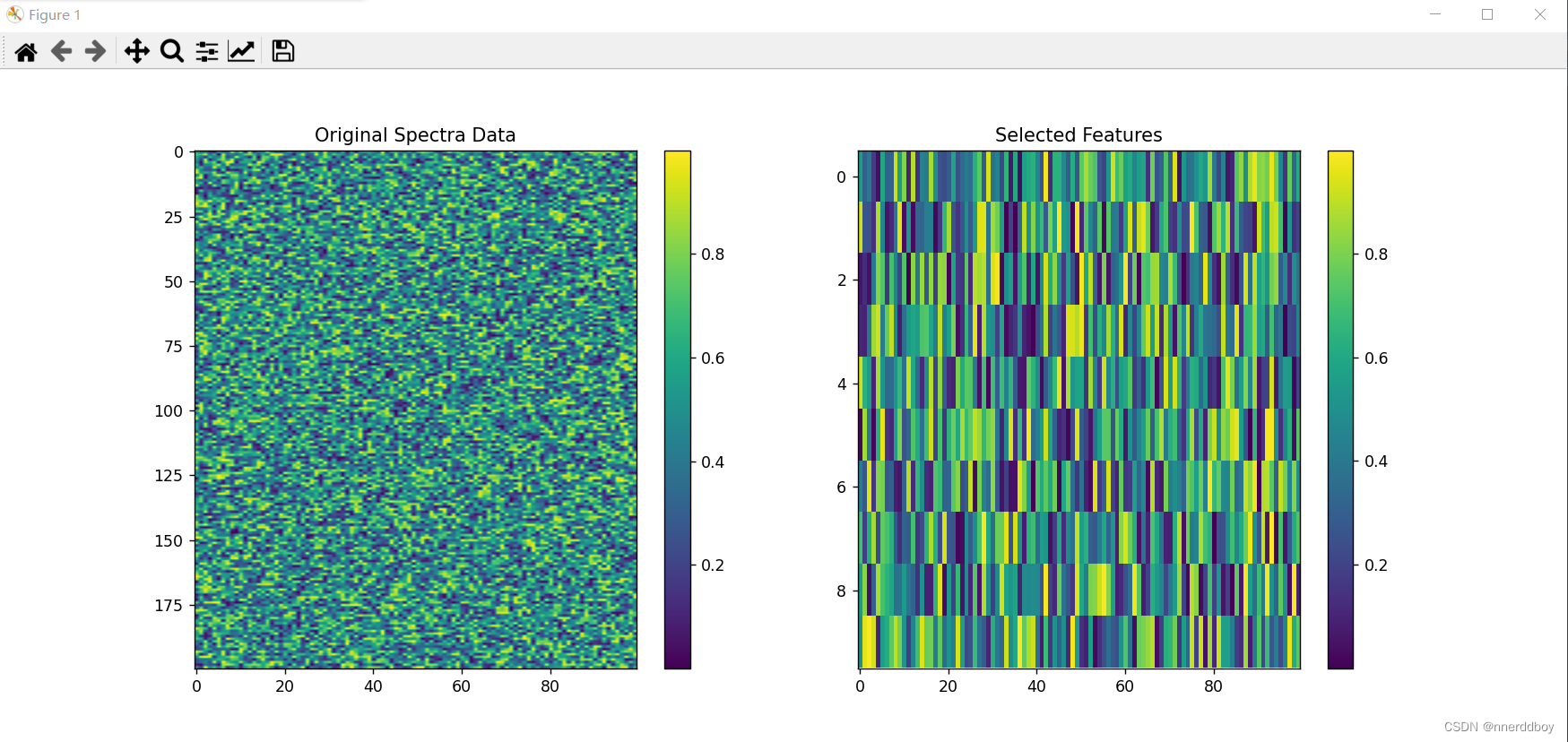
五、随机蛙跳算法（Random-Frog）

(1)原理详解

        想象你在一个巨大的草地上寻找宝藏，草地上有很多可能藏有宝藏的地点，但你没有地图，所以不知道宝藏确切在哪儿。

        这就是随机蛙跳算法的情况，其中宝藏相当于对我们很重要的信息或特征（就像在光谱数据中找到最重要的波长点），而草地的每个地点代表数据集中的一个特征。

        现在，随机蛙跳算法的过程大概是这样的：

1. 随机选择：你闭上眼睛，随机地跳到草地上的某个点，就好像是“蛙跳”一样。

2. 挖掘尝试：在这个点上，你用铲子挖挖看，看能不能找到宝藏。

3. 记录结果：如果你觉得这个点下面可能有宝藏，你就在地图上做个标记，这样你就知道这个地方值得以后再来挖掘。

4. 重复过程：你重复闭眼随机跳跃和挖掘的过程很多次。

5. 分析结果：最后，你打开眼睛，看看哪些地方被标记了很多次。这些地方很可能就是藏宝的热点，因为你多次随机挖掘都觉得那里可能有宝藏。

6. 做出判断：最后，你决定专注于那些被反复标记的地点进行深入挖掘，因为这样做找到宝藏的可能性最大。

        用这个比喻来理解，随机蛙跳算法通过反复随机选择一些特征，并评估它们对结果的影响（有没有“挖到宝藏”），然后总结哪些特征最有可能是我们寻找的“宝藏”。这种方法不需要预先知道哪里有宝藏，而是通过重复随机尝试和评估来找到最好的线索。

def random_frog(X, y, num_selected_features, num_iterations=100):# 保存特征的重要性分数feature_importances = np.zeros(X.shape[1])# 随机蛙跳迭代过程for _ in range(num_iterations):# 选择一个随机特征子集selected_features = np.random.choice(X.shape[1], num_selected_features, replace=False)# 创建一个随机森林分类器model = RandomForestClassifier(n_estimators=10, random_state=0)# 使用选定的特征和随机森林进行训练model.fit(X[:, selected_features], y)# 更新特征的重要性分数feature_importances[selected_features] += model.feature_importances_# 根据重要性分数选择最重要的特征important_features = np.argsort(feature_importances)[-num_selected_features:]return important_features

        该函数使用了一个简化的随机蛙跳过程来选择特征。在这个过程中，我们在每个迭代步骤中随机选择一个特征子集，并用随机森林算法训练一个模型，然后基于模型输出的特征重要性分数来更新这些特征的总重要性评分。在多次迭代之后，我们选择那些具有最高累积重要性分数的特征。

(2)完整代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier# 假设光谱数据集 X 和对应的类别标签 y
# 生成一些示例数据作为光谱数据
np.random.seed(0)
X = np.random.rand(100, 200)  # 100个样本，200个波长特征
y = np.random.randint(0, 2, 100)  # 100个样本的类别标签（0或1）# 定义一个简化的 Random Frog 方法
def random_frog(X, y, num_selected_features, num_iterations=100):# 保存特征的重要性分数feature_importances = np.zeros(X.shape[1])# 随机蛙跳迭代过程for _ in range(num_iterations):# 选择一个随机特征子集selected_features = np.random.choice(X.shape[1], num_selected_features, replace=False)# 创建一个随机森林分类器model = RandomForestClassifier(n_estimators=10, random_state=0)# 使用选定的特征和随机森林进行训练model.fit(X[:, selected_features], y)# 更新特征的重要性分数feature_importances[selected_features] += model.feature_importances_# 根据重要性分数选择最重要的特征important_features = np.argsort(feature_importances)[-num_selected_features:]return important_features# 使用随机蛙跳方法选择特征
selected_features = random_frog(X, y, num_selected_features=20)# 绘制原始数据
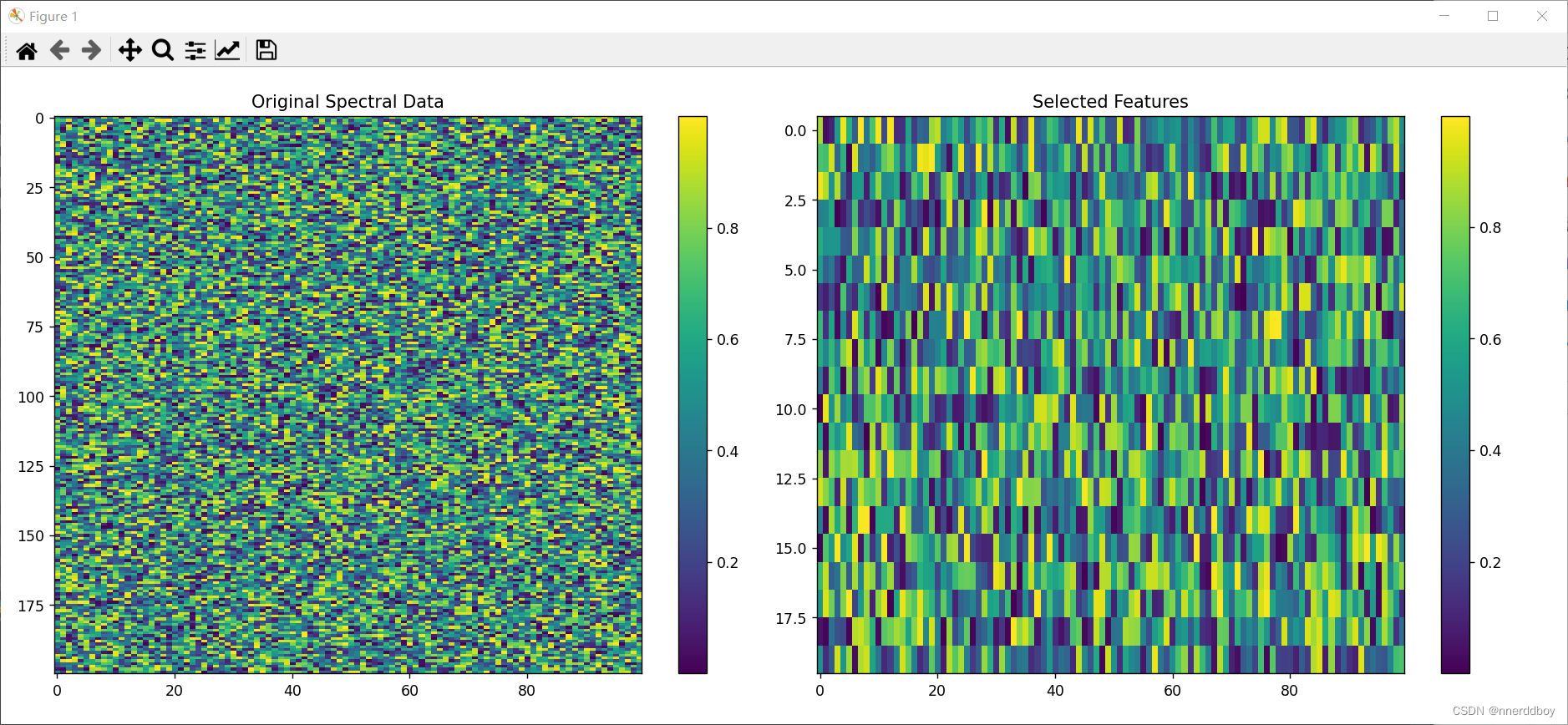
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
plt.imshow(X.T, aspect='auto', cmap='viridis')
plt.colorbar()
plt.title('Original Spectral Data')# 绘制经过特征选择后的数据
plt.subplot(1, 2, 2)
selected_data = X[:, selected_features]
plt.imshow(selected_data.T, aspect='auto', cmap='viridis')
plt.colorbar()
plt.title('Selected Features')plt.tight_layout()
plt.show()

(3)运行结果