2326. 王者之剑（网络流，最小割，最大权独立集，最小点权覆盖）-编程知识

活动 - AcWing

给出一个 n×m 网格，每个格子上有一个价值 vi,j 的宝石。

Amber 可以自己决定起点，开始时刻为第 0 秒。

以下操作，在每秒内按顺序执行。

若第 i 秒开始时，Amber 在 (x,y)，则 Amber 可以拿走 (x,y) 上的宝石。
在偶数秒时（i 为偶数），则 Amber 周围 4 格的宝石将会消失。
若第 i 秒开始时，Amber 在 (x,y)，则在第 (i+1) 秒开始前，Amber 可以马上移动到相邻的格子 (x+1,y),(x−1,y),(x,y+1),(x,y−1) 或原地不动 (x,y)。

求 Amber 最多能得到多大总价值的宝石。

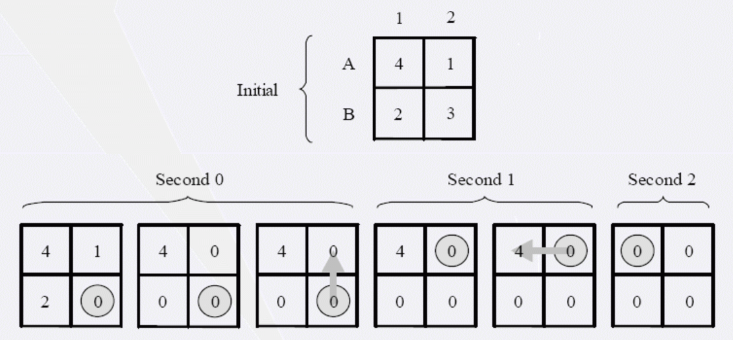
上图给出了一个 2×2 的网格的例子。

在第 0 秒，首先选择 B2 进入，取走宝石 3；由于是偶数秒，周围的格子 A2,B1 的宝石 1,2 消失；向 A2 走去。

在第 1 秒，由于 A2 的宝石已消失，无宝石可取；向 A1 走去。

在第 2 秒，取走 A1 的宝石 4。

全程共取得 2 块宝石：宝石 3 和宝石 4。

输入格式

第一行包含两个整数 n,m。

接下来 n 行，每行包含 m 个整数，用来描述宝石价值矩阵。其中第 i 行第 j 列的整数表示 vi,j。

输出格式

输出可拿走的宝石最大总价值。

数据范围

1≤n,m≤100
1≤vi,j≤1000

输入样例：

2 2
1 2
2 1

输出样例：

解析：

最大权独立集=总权值 - 最小权点覆盖

性质：

（1）只能在偶数秒拿宝石

（2）不可能拿走相邻格子上的宝石

如果将相邻两个格子之间都连一条边，则能拿的宝石一定是一个独立集。而每个格子上都有一个权值，又是求获得宝石的最大值，可以发现本题已经非常像最大权独立集问题。

到此已经能将任意一个合法方案对应到二分图中的一个独立集。但是还需要证明任意一个二分图中的独立集都能对应到一个合法方案。其实对于任意一个独立集都能构造出一个合法方案，可以从最左上角的一个有宝石的格子开始走，依次去取别的宝石，假设当前距离下一个宝石还剩两步，停下来判断一下，如果当前是偶数秒，直接走过去拿宝石，如果当前是奇数秒，原地停一秒再走过去拿宝石。且保证每次都优先取最近的宝石。这样的行走方案一定能将独立集中的所有宝石拿走，可以自行按照以上思路证明，这里的构造方式非常多，只要掌握好停顿一秒的精髓就能随便构造。

由此得出任意一个合法方案和任意一个独立集都是一一对应的，因此要想求最大能取的宝石价值就等价于求最大权独立集，而最大权独立集 = 总权值 − 最小权点覆盖集。

最大权点独立集的相关概念

独立集： 给定一个一般图 G(V,E)，选出图中的某一个点集，使得选出的所有点之间不存在边，则将这个点集称为原图的独立集

-------------------------------------------------------------------------------------------------------------------

最大权独立集：给定一个有向图 G(V,E)，每个点上有一个非负权值，而图中权值和最大的独立集称为最大权独立集

-------------------------------------------------------------------------------------------------------------------

如何求最大权独立集：

最大权独立集和最小权点覆盖集问题一样，在一般情况下都是一个 NP 完全问题（NPC 问题），只能用爆搜来解决，但是在二分图中却具有非常高效的特殊做法。

结论：最大权点独立集 = 所有点的总权值 − 最小权点覆盖集

若整个点集是 V，点覆盖集是 V1，那么补集就是 V2=V−V1。

这里有一个性质，任意一个点覆盖集的补集都一定是独立集。这里进一步证明这个性质。可以用反证法，假设点覆盖集 V1 的补集 V2 不是独立集，说明 V2 中存在两个点 u,v 之间存在一条边 (u,v)。由于 V1 同样是 V2 的补集，说明 V1 中一定不包含 u,v 这两个点，那么 (u,v) 这条边的两个点就都不在 V1 中，即 V1 不是一个点覆盖集，与条件矛盾，反证得出任意一个点覆盖集的补集都是一个独立集。

以上性质反过来，任意一个独立集的补集都一定是点覆盖集。同样用反证法，假设独立集 V2 的补集 V1 不是点覆盖集，就必然存在一条边 (u,v)，使得这条边的两个点 u,v 都不在 V1，即一定在 V2 中，也就说明 V2 中存在两个点 u,v 之间是有边的，所以 V2 就不是一个独立集，反证得出任意一个独立集的补集都是一个点覆盖集。

可以发现独立集和点覆盖集之间是存在补集这样一个对应关系的，然后看一下两者之间的数量关系，数量关系就非常明显了，因为 V1 和 V2 互为补集，所以两个集合的权值总和就等于所有点的权值和，即 w(V1)+w(V2)=w(V)，而 w(V) 是一个固定值，因此想让 w(V2) 取最大，w(V1) 就必然取到最小，因此要想求最大全独立集，只需要求一下最小权点覆盖集，最小权点覆盖集的补集就是最大权独立集，由此得证结论。

——————————————————————————————————————

作者：小小_88
链接：https://www.acwing.com/file_system/file/content/whole/index/content/6381812/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

（非常棒的作者，建议看原题解）

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 1e4 + 10, M = (2e4 + N ) * 2 + 10, INF = 0x3f3f3f3f;
int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];int get(int a, int b) {return (a - 1) * m + b;
}void add(int a, int b, int c) {e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++;e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}bool bfs() {int hh = 0, tt = 0;memset(d, -1, sizeof d);q[0] = S, d[S] = 0, cur[S] = h[S];while (hh <= tt) {int t = q[hh++];for (int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if (d[j] == -1 && f[i]) {d[j] = d[t] + 1;cur[j] = h[j];if (j == T)return 1;q[++tt] = j;}}}return 0;
}int find(int u, int limit) {if (u == T)return limit;int flow = 0;for (int i = cur[u]; i != -1 && flow < limit; i = ne[i]) {int j = e[i];cur[u] = i;if (d[j] == d[u] + 1 && f[i]) {int t = find(j, min(f[i], limit - flow));if (!t)d[j] = -1;f[i] -= t, f[i ^ 1] += t, flow += t;}}return flow;
}int dinic() {int ret = 0, flow;while (bfs())while (flow = find(S, INF))ret += flow;return ret;
}int main() {int dx[] = { 0,0,1,-1 }, dy[] = { 1,-1,0,0 };cin >> n >> m;S = 0, T = m * n + 1;memset(h, -1, sizeof h);int tot = 0;for (int i = 1; i <= n; i++) {for (int j = 1,a; j <= m; j++) {scanf("%d", &a);if (i + j & 1) {add(S, get(i, j), a);for (int k = 0; k < 4; k++) {int x = i + dx[k], y = j + dy[k];if (x > 0 && x <= n && y > 0 && y <= m)add(get(i, j), get(x, y), INF);}}else add(get(i, j), T, a);tot += a;}}printf("%d\n", tot - dinic());return 0;
}