Top-k问题
- 方法一:堆排序(升序)(时间复杂度O(N*logN))
- 向上调整建堆(时间复杂度:O(N * logN) )
- 向下调整建堆(时间复杂度:O(N) )
- 堆排序代码
- 方法二:直接建堆法(时间复杂度:O(N+k×logN) ≈ O(N))
- 方法三:建一个k个数的小堆(时间复杂度O(k+(N-k)×logk)≈O(N))
方法一:堆排序(升序)(时间复杂度O(N*logN))
升序堆排序的一般思路就是将给定的一组数据放在堆得数据结构当中去,然后进行不断被的取堆顶元素放在数组当中,不断地pop(删除)。但是这种方法太麻烦了,自己还要手写一个堆的数据结构以及一些接口函数,还要创建数组等,显然不是最优解。
接上文的写的两种调整方式,向上调整和向下调整。 详细见
思路:
①可以用向上调整或者向下对原数组进行调整,也就是建一个大堆(排升序大堆后面讲为啥)
②接下来利用堆删除的原理,将堆顶的数据和数组最后一个交换(也就是将堆顶和堆尾的数据进行交换),然后就相当于最大的数放在了最后一个位置,所以最后一个位置的数据确定了,接下来对剩下的数据进行向下调整,再重复以上操作。
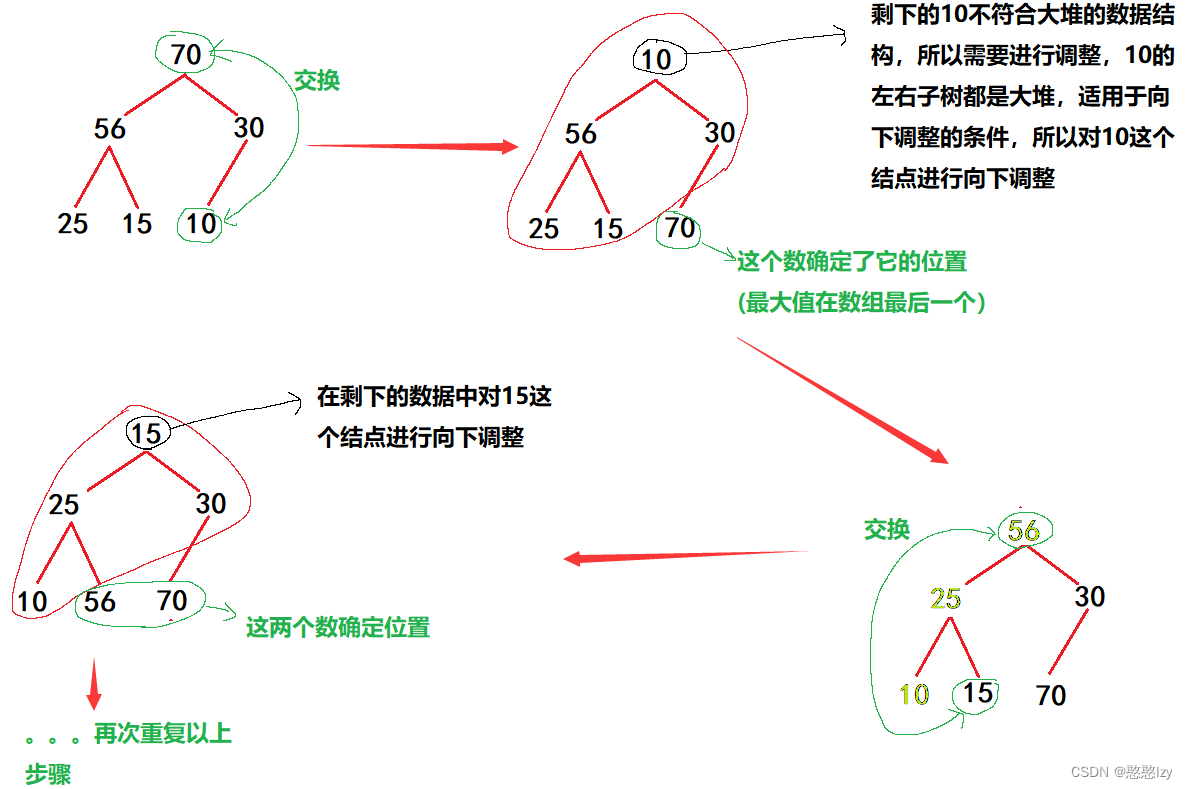
ps:排升序建大堆而不是小堆的原因,反证思路来看,若建小堆的话,最小的数据在第一个,第一个数据确定了,但是剩下的数据很暖再重新调整成为一个新的小堆的数据结构,所以排升序建小堆很难是实现
向上调整和向下调整都可以完成建堆的操作,但是他们的时间复杂度有所不同,接下来讲一下他们的取舍。
向上调整建堆(时间复杂度:O(N * logN) )
for (int i = 1; i < n; i++){AdjustUp(a, i);}
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):
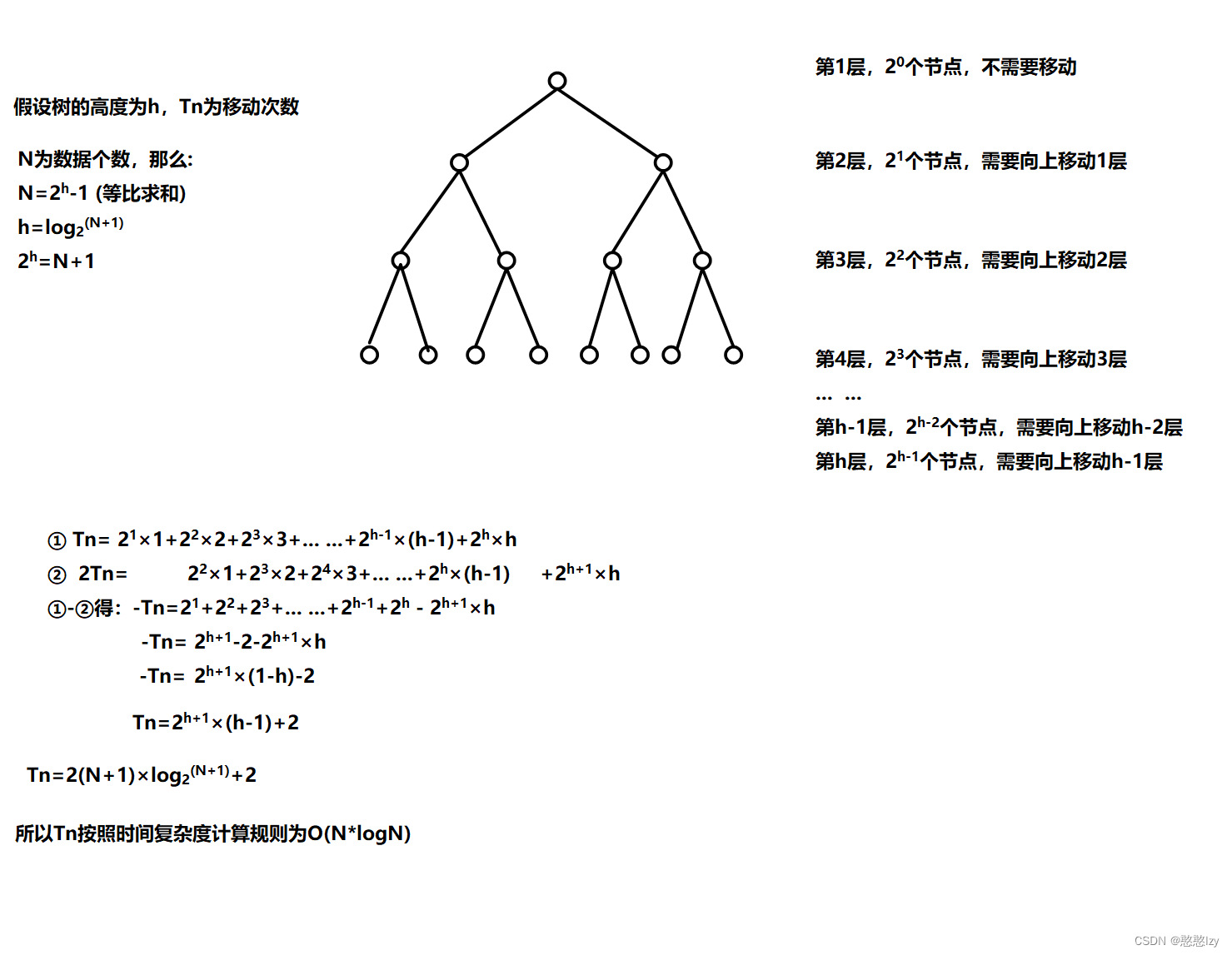
向下调整建堆(时间复杂度:O(N) )
for (int i = (n - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);//a是堆的数组,n是防止数组越界的数组数据个数,i是开始向下调整的位置}
向下调整建堆得思路:从第一个非叶子结点开始从数组得后面向前面一个一个进行调整

复杂度证明:
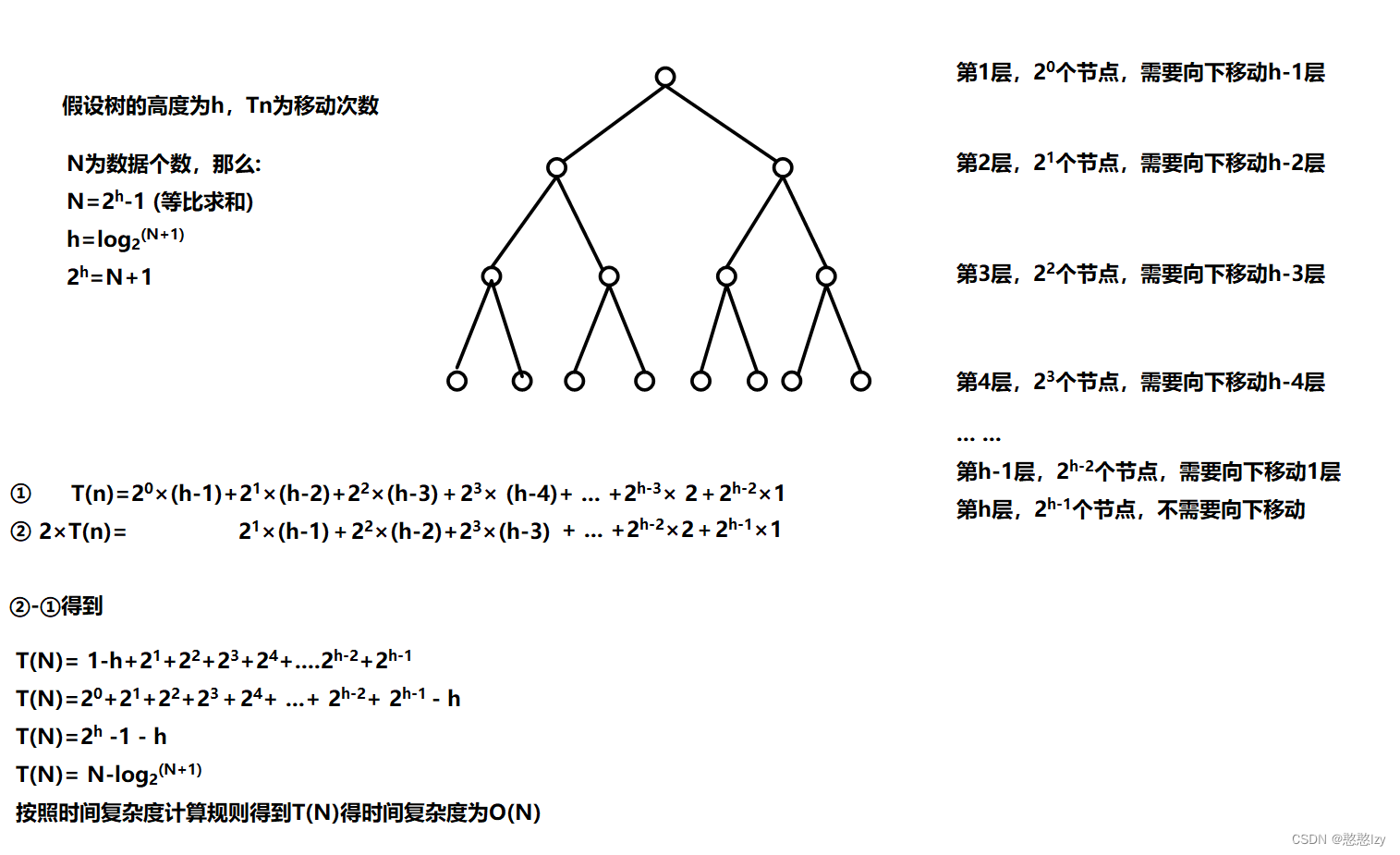
看到这里很容易发现向下调整方法建堆得时间复杂度更加合适
堆排序代码
// 对数组进行堆排序
void HeapSort(int* a, int n)
{//思路:向上调整方法建堆建堆//>这里排升序要建大堆,因为建小堆的话,接下来排升序第一个数据好处理,//但是剩下的数据重新排成堆的话关系全都乱了//所以这时候建大堆,和删除的思路一样,首先交换堆顶和堆尾,这时候最大的数据放到了最后一个位置//然后将前面n-1个数据看成新的堆进行向下调整,然后再找次大的数放在倒数第二的位置//建堆有两种方式 向上调整建堆和向下调整建堆,时间复杂度分别为O(N*logN)和O(N)//向上调整建堆 建堆时间复杂度 O(N*logN)/*for (int i = 1; i < n; i++){AdjustUp(a, i);}*///向下调整建堆 时间复杂度为O(N)//向下调整的条件是调整节点的左右子树都为大堆或者小堆//所以从下边开始进行向下调整(大堆),这时候大的数会慢慢上浮,最先调整的位置不能是叶子节点,那样会重复很多操作//应该从最后一个父亲节点开始进行向下调整 最后一个父亲节点的下标为 (n-1)/2,然后按数组下标的顺序递减进行调整for (int i = (n - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);//a是堆的数组,n是防止数组越界的数组数据个数,i是开始向下调整的位置}while (--n) //排序的时间复杂度为O(N*logN){//此处为--n的原因:一共有n个数据,循环一次确定一个数据的位置,循环n-1次之后就可以确定n-1个数据的位置,// 前面已经确定了n-1个位置,最后一个数据的位置也已经确定,所以当n=0的时候的那一次循环可以不需要进行就可以// //此时n已经自减1,所以此时n就为堆尾数据,且n为下一个新堆的数据个数,所以后面向下调整直接传参nSwap(&a[0], &a[n]);//交换堆顶和堆尾的数据AdjustDown(a, n, 0);//n为新堆的数据个数}//总结:堆排序的时间复杂度为O(N*logN),因为堆排序有两个步骤①建堆②排序//建堆向上调整建堆的时间复杂度为O(N*logN),向下调整建堆的时间复杂度为O(N),相对较快,//但是排序的时间复杂度都为O(N*logN),所以决定了堆排序的时间复杂度为O(N*logN)。
}
方法二:直接建堆法(时间复杂度:O(N+k×logN) ≈ O(N))
思路:有了堆排序中的向下调整建堆法,可以将这N个数建一个小堆,然后取堆顶元素打印,然后Pop(删除)k次这样稍微简单些,但是当数据个数N太大得时候,对内存得要求很大,会占用很多内存,因为这种方法中,需要在堆区中创建一个N个数据的动态1数组,然后将数据放在数组当中去,因为如果在N很大的情况下,有可能你的设备内存并没有那么大。所以这是这种方法的缺点。
一般数据都是放在磁盘或者文件中,所以我接口函数可以传文件流
//创建随机n个数据
void CreatData(int n)
{int k = 10;srand((unsigned int)time(NULL));//调用rand()的返回值形成随机数必须调用srand函数//srand函数的形参为unsigned int类型的,且形参为不断变化的数才可以生成为随机数//所以形参传参为时间戳函数time,time函数的形参得传NULLconst char* file = "data.txt";FILE* pf = fopen(file, "w");if (pf == NULL){perror("fopen fail\n");return;}else{printf("打开成功\n");}for (int i = 0; i < n; i++){fprintf(pf, "%d\n", rand() % 10000);}fclose(pf);//关闭文件pf = NULL;
}//打印n个数据中最大的k个数据
void PrintTop1(const char* file, int k, int n)//n是数据个数
{FILE* pf = fopen(file, "r");if (pf == NULL){perror("PrintTop fopen fail");return;}//1.把n个数建大堆int* top = (int*)malloc(sizeof(int) * n);//创建一个动态数组存放堆的数据if (top == NULL){perror("top malloc fail\n");return;}//读取n个数放在堆当中去for (int i = 0; i < n; i++){fscanf(pf, "%d", &top[i]);}//向下调整建大堆for (int i = (n - 1) / 2; i >= 0; i--){AdjustDown(top, n, i);}//打印 k次堆顶元素for (int i = 0; i < k; i++){printf("%d ", top[0]);//打印堆顶元素Swap(&top[0], &top[n - i]);AdjustDown(top, n - i - 1, 0);//这里交换后的那个数据不能算入内}
}
//测试CreatData(10000000);//创建数据
PrintTop1("data.txt", 10,10000000);//这里测试时候可以直接只改PrintTop1中n的大小,因为前面CreatData创建数据会花费很多时间,导致第二个函数并不能直接运行//CreatData(10000000);//创建数据
//PrintTop1("data.txt", 10, 100000000);//CreatData(10000000);//创建数据
//PrintTop1("data.txt", 10, 1000000000);代码先放在这里,接下来我来验证:
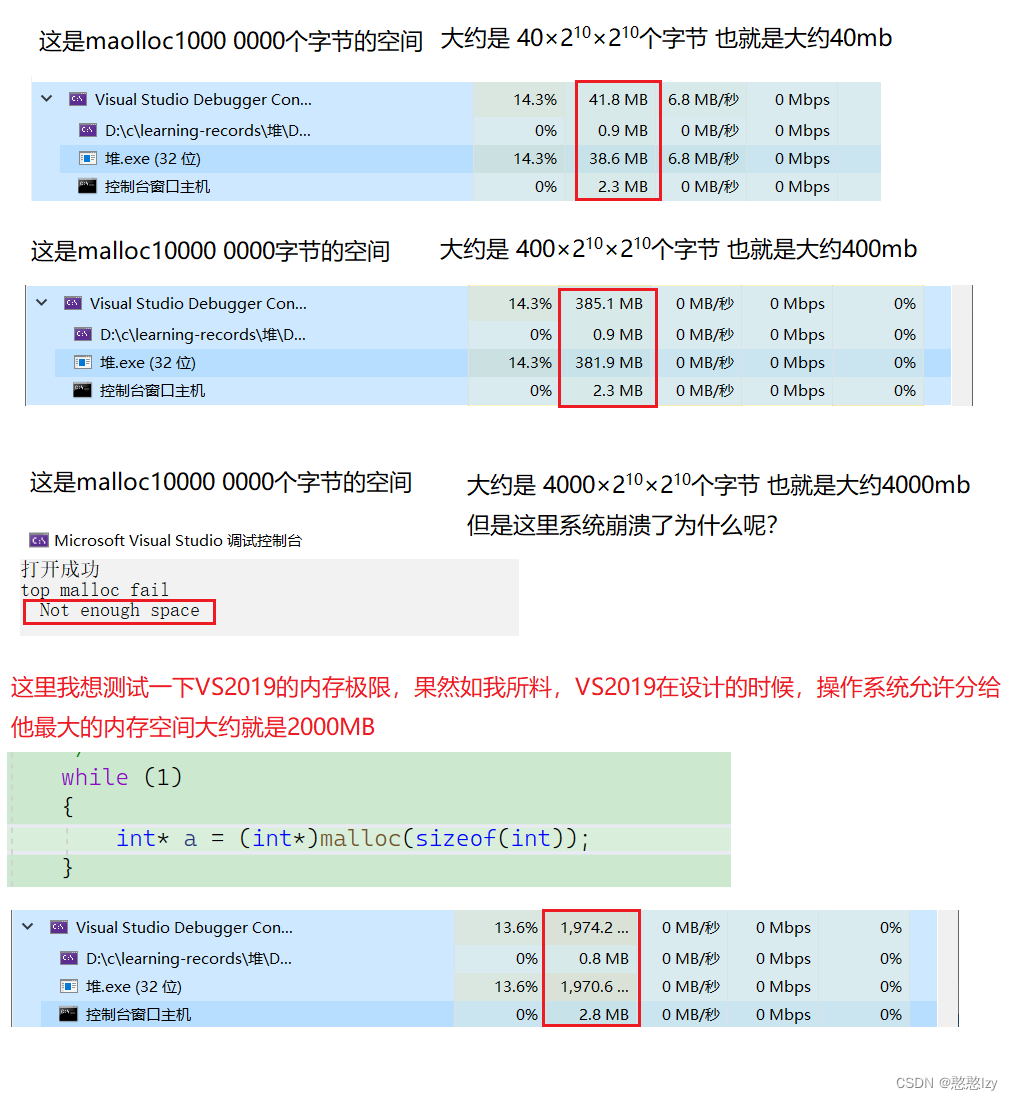
所以这种方法当数据N很大的时候并不可取
方法三:建一个k个数的小堆(时间复杂度O(k+(N-k)×logk)≈O(N))
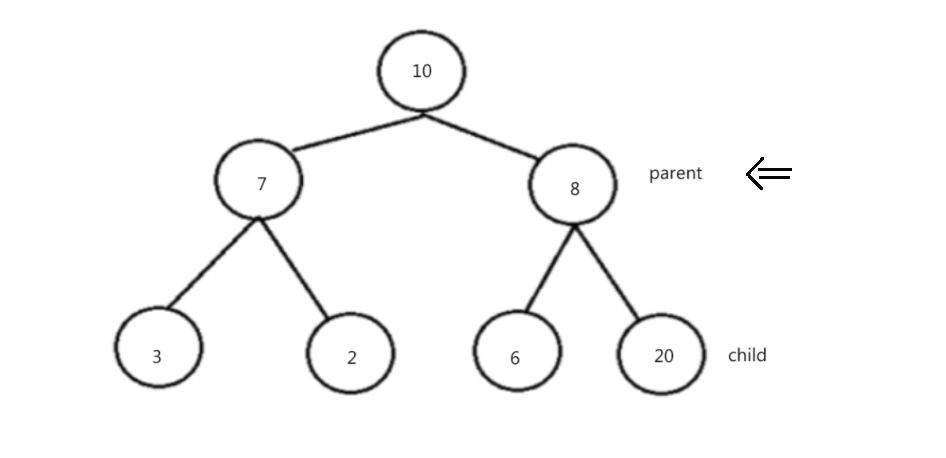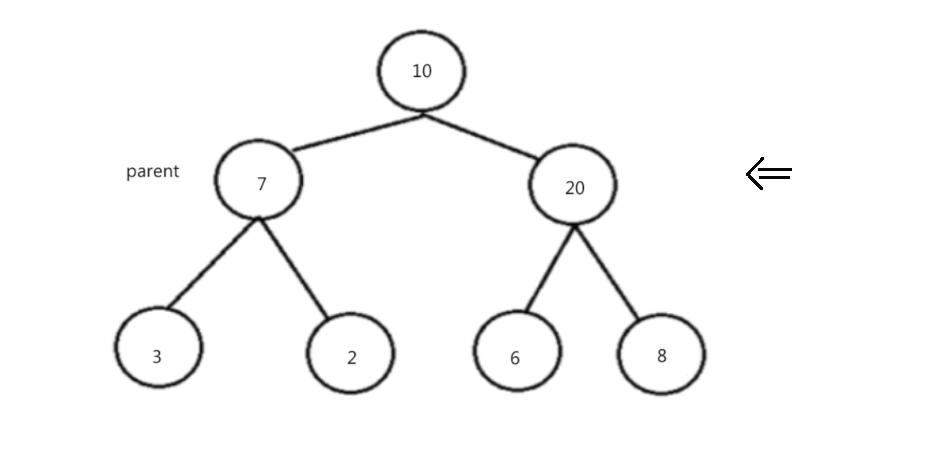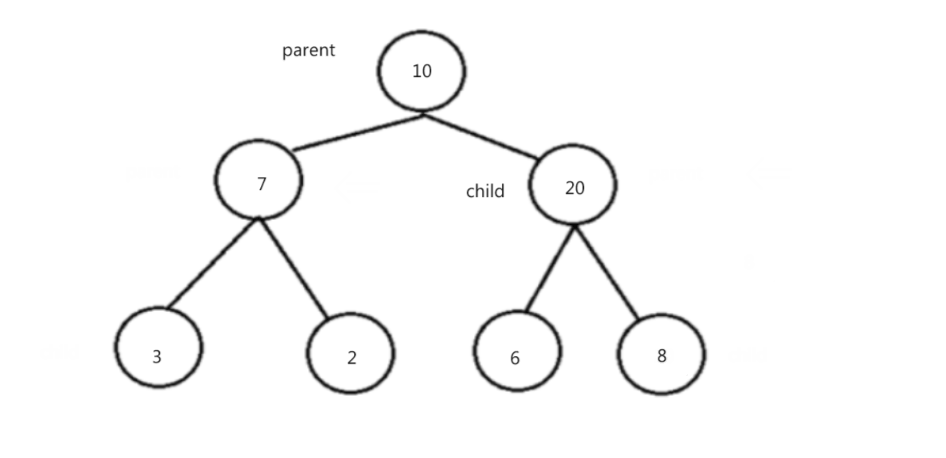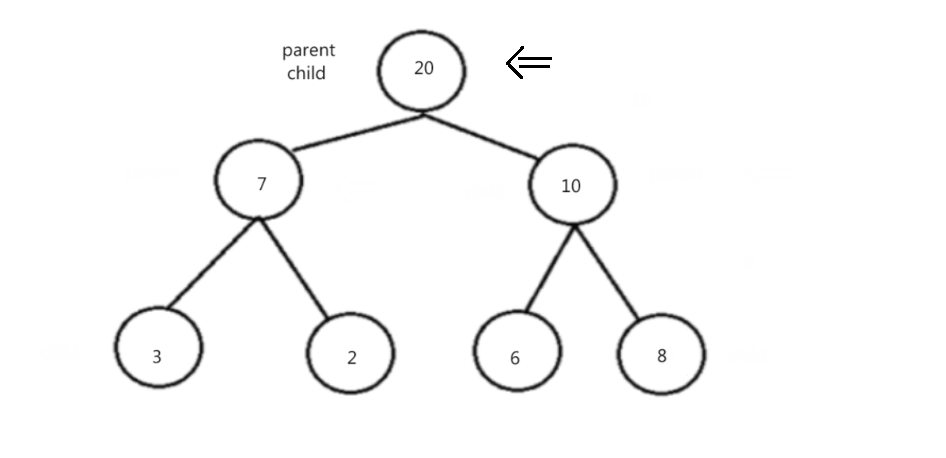
思路:取前k个数建立一个k个数的小堆,然后遍历剩下的所有数据,并和堆顶进行比较,只要比堆顶大就和堆顶交换,然后进行调整,然后进行循环,遍历结束之后也就证明这k个数为所要求的k个数。例如:
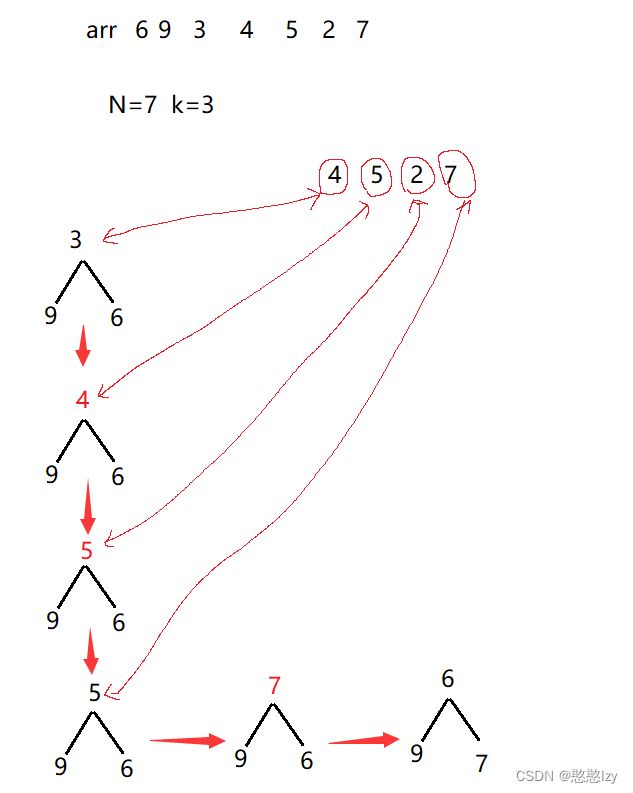
代码:
//小堆的向下调整 和大堆的向下调整一样
void AdjustDownSmall(HPDateType* a, int n, int parent)//向下调整(小堆) 时间复杂度O(logN)
//向下调整的条件是调整节点的左右子树都为大堆或者小堆
//思路为从下标为parent位置开始向下的孩子节点不断比较进行调整,直到最后一个数据,
//所以需要传参堆的有效数据个数n
{int leftchild = parent * 2 + 1;while (leftchild < n)//{int rightchild = parent * 2 + 2;if (rightchild < n && a[leftchild] > a[rightchild]){//判断一下该父亲节点是否有右孩子,防止数组越界//默认左孩子小于右孩子//若右孩子小于左孩子则交换下标Swap(&leftchild, &rightchild);}if (a[parent] > a[leftchild]){Swap(&a[parent], &a[leftchild]);//若不符合堆的要求则交换parent = leftchild;//将原父亲数据对应下标也赋值过来leftchild = parent * 2 + 1;//新的孩子的下标}else//若符合堆的要求就退出循环{break;}}
}//Top-k 问题 取前k个较大的数
void PrintTop(const char* file, int k)//把文件传进来和需要找的前k个数
{FILE* pf = fopen(file, "r");if (pf == NULL){perror("PrintTop fopen fail");return ;}//1.把前k个数建小堆int* top = (int*)malloc(sizeof(int) * k);//创建一个动态数组存放堆的数据if (top == NULL){perror("top malloc fail\n");return;}//从文件中读取k个数据放在数组中for (int i = 0; i < k; i++){fscanf(pf, "%d", &top[i]);}for (int i = (k - 1) / 2; i >= 0; i--){AdjustDownSmall(top, k, i);}//2.遍历剩下的n-k个数并与堆顶作比较,若比堆顶大则交换然后再进行向下调整int val = 0;int ret = fscanf(pf, "%d", &val);while (ret != EOF){if (val > top[0]){Swap(&val, &top[0]);AdjustDownSmall(top, k, 0);}ret = fscanf(pf, "%d", &val);}//打印数组for (int i = 0; i < k; i++){printf("%d\n", *(top+i));//printf("%d\n", top[i]);//会报错C6385//像数组一样在连续内存空间存储的多个数据才使用下标法//这种应该是编译器问题 具体不清楚}free(top);top = NULL;fclose(pf);pf = NULL;
}
分析:对比时间复杂度方法二和方法三的时间复杂度都差不多,方法三在N为很大的情况下,所用内存空间是取决于k的,因为k一般是一个很小的数一般不会很大,导致内存崩溃。
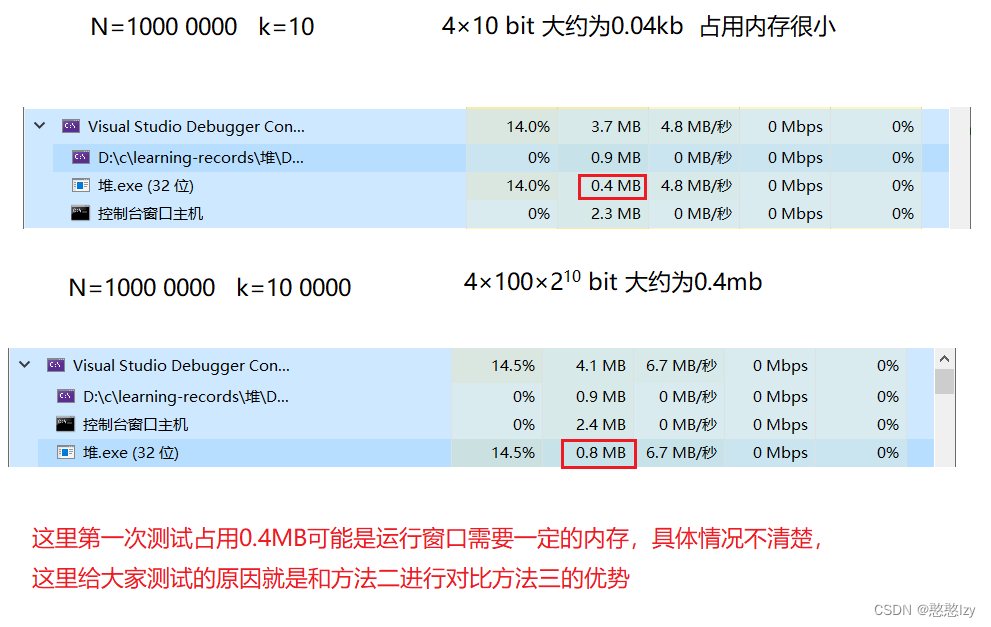
方法二 方法三自己实测其实时间上,对于1000 0000个数据的时候运行的时候都会大约等待个5 6秒,所以他们的时间复杂度大差不差,优势在于空间的使用。