1 B树介绍
B树(英语:B-tree),是一种在计算机科学自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。B树,概括来说是一个一般化的二叉搜索树(binary search tree)一个节点可以拥有2个以上的子节点。与自平衡二叉查找树不同,B树适用于读写相对大的数据块的存储系统,例如磁盘。B树减少定位记录时所经历的中间过程,从而加快访问速度。B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。
那为什么要使用 B-树呢(或者说为啥要有 B-树呢)?
要解释清楚这一点,我们假设我们的数据量达到了亿级别,主存当中根本存储不下,我们只能以块的形式从磁盘读取数据,与主存的访问时间相比,磁盘的 I/O 操作相当耗时,而提出 B-树的主要目的就是减少磁盘的 I/O 操作。大多数平衡树的操作(查找、插入、删除,最大值、最小值等等)需要 O(ℎ) 次磁盘访问操作,其中 ℎ 是树的高度。但是对于 B-树而言,树的高度将不再是logn(其中 n是树中的结点个数),而是一个我们可控的高度 ℎ (通过调整 B-树中结点所包含的键【你也可以叫做数据库中的索引,本质上就是在磁盘上的一个位置信息】的数目,使得 B-树的高度保持一个较小的值)。一般而言,B-树的结点所包含的键的数目和磁盘块大小一样,从数个到数千个不等。由于B-树的高度 h 可控(一般远小于logn ),所以与 AVL 树和红黑树相比,B-树的磁盘访问时间将极大地降低。
平衡二叉排序树是利用插入的成本缓解查找效率---------->红黑树来解决(最长子树不超过最短子树的2倍。数据量大的时候,树会很深,查找次数变多)----------->B树(多叉,多路查找树)
动画显示树调整的网站:Data Structure Visualization
2 B树特点
B树是一种平衡的多叉树,通常我们说m阶的B树,它必须满足如下条件:
- 每个节点最多有m个子节点。
- 每一个非叶子节点(除根节点)最少有[m/2]个子节点。
- 如果根节点不是叶子节点,那么它至少有两个子节点。
- 有k个子节点的非叶子节点拥有k-1个键,且升序排列,满足k[i] < k[i + 1]
- 每个节点至多包含2*k-1个键。
- 所有的叶子节点都在同一层。
- 每个节点的结构是

其中:
n记录这个节点关键字的个数;
P0存储的是第一个孩子的地址,P1存储的是第二个孩子的地址,以此类推。。。。。。
K1是第一个关键字,K2是第二个关键字,以此类推。。。。。。
B树中一个节点的子节点数目的最大值,用m表示,假如最大值为4,则为4阶,如下图
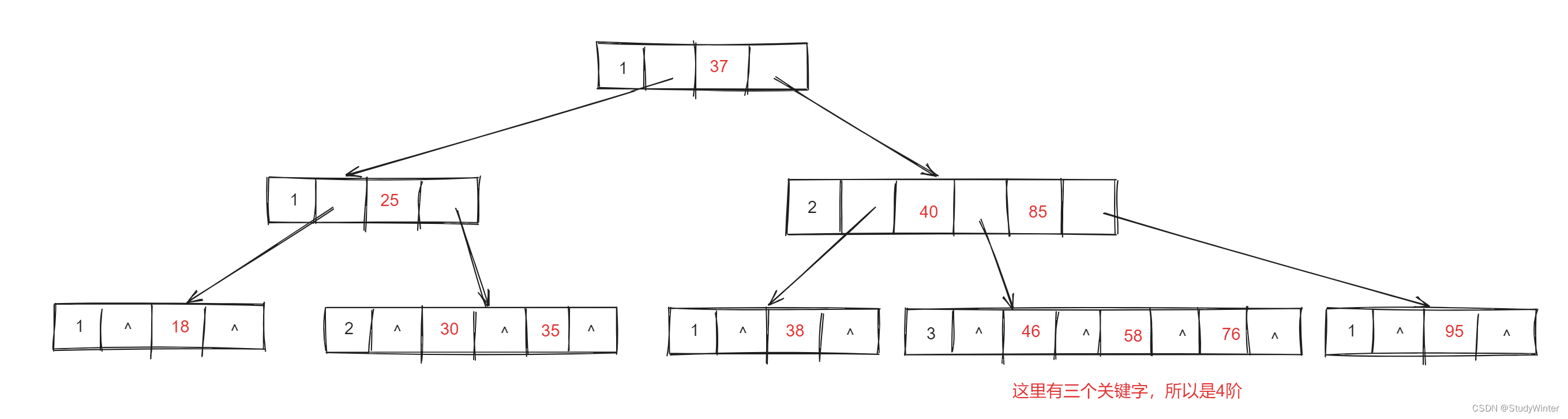
性质:
- 每个节点最多有m个子节点。
- 每一个非叶子节点(除根节点)最少有[m/2]个子节点。
- 如果根节点不是叶子节点,那么它至少有两个子节点。
- 有k个子节点的非叶子节点拥有k-1个键,且升序排列,满足k[i] < k[i + 1]
- 每个节点至多包含2*k-1个键。
- 所有的叶子节点都在同一层。
- 满足n叉排序树
3 B树的增删改查
磁盘预读
内存跟磁盘发生数据交互的时候,一般情况下有一个最小的逻辑单元,称之为页,datapage
页一般由操作系统决定是多大,一般是4k或者8k,我们在数据交互时,可以取页的整数倍来进行读取。
电脑的文件都是datapage的整数倍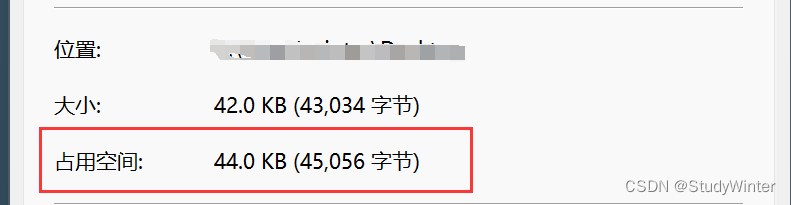
每个节点放在磁盘块里,用B树做索引,这个磁盘大小是16k


三层数据。
对比B树和B+树
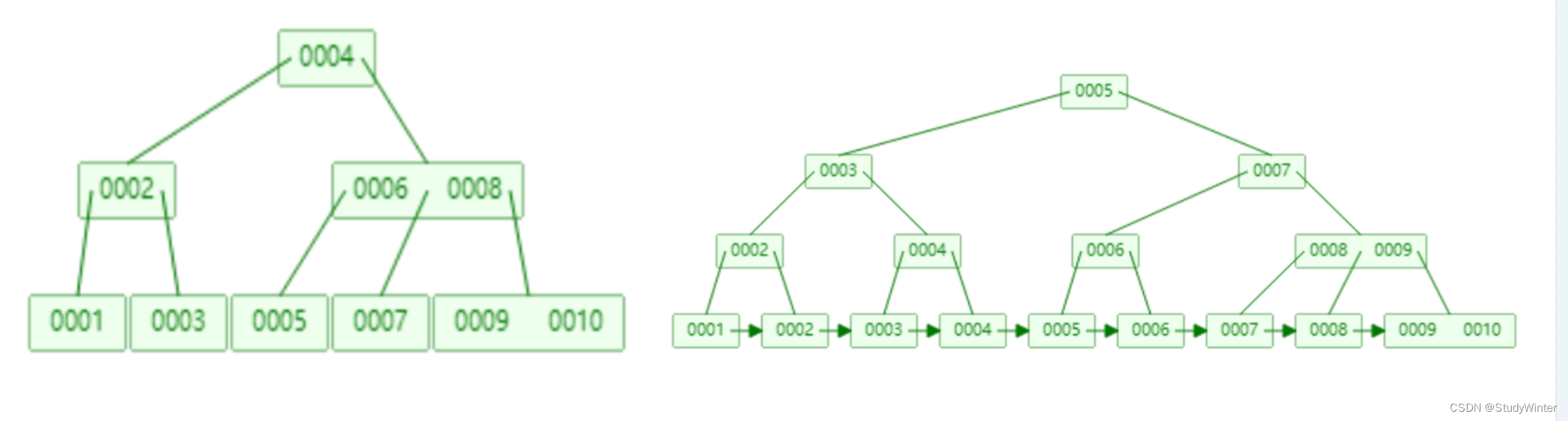
有一个很重要的不同是:B+树的数据都存在叶子节点上。
参考:
[1] https://zh.wikipedia.org/zh-hans/B%E6%A0%91
[2] 图解:什么是B树?(心中有 B 树,做人要虚心)一文读懂B-树 - 知乎 (zhihu.com)
[3] B 树 - OI Wiki (oi-wiki.org)
[4] 终于把B树搞明白了(四)_B树的删除操作_哔哩哔哩_bilibili
[5] notes/docs/B树和B+树详解.md at master · wardseptember/notes · GitHub