目录

题目介绍： 

 算法原理：

鸽巢原理：

如何找到环里元素：

代码实现：

---

题目介绍： 

题目链接：. - 力扣（LeetCode）

 算法原理：

我先简单举两个例子：

19： 

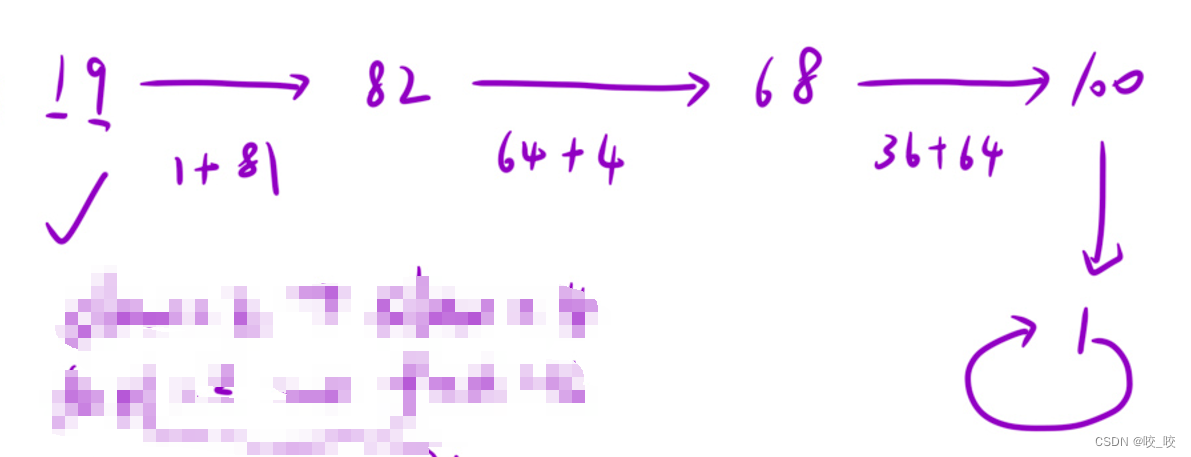
2：

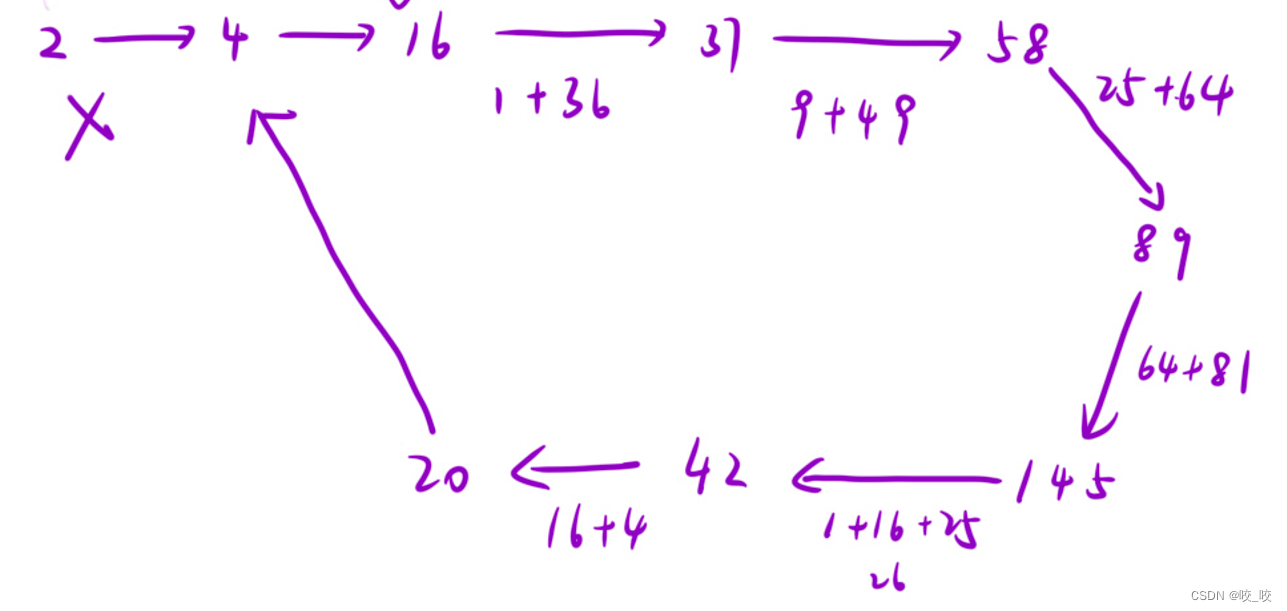
  其实大部分人拿到这道题，第一感觉就是如果是快乐数，只需利用循环一步步求解，最后如果有一次结果为1时，就是快乐数，可是如果不是快乐数，岂不是要一直循环下去？这道题最重要的一点就是如果不是快乐数最后的数据是必定成环的，证明需要利用鸽巢原理：

鸽巢原理：

如果有n个巢穴，n+1只鸽子，那么必定会有一个巢血有2个或以上的鸽子。

这个原理很简单，我们利用它来证明一下这道题若不是快乐数必定成环：

利用极限法：

来看看这道题数据的最大值2的31次方=2147483648，不妨再去大点直接取9999999999，我们看看这个数经历一次变化（替换为该数每一位的平方和）后会变成多少，也就是9*9*10=810，这个最大的数经历一次变化后变为810，那么比这个数小的数经历一次变化肯定不会大于810，所以我们的巢就是1-810，也就是有810个巢，那我们的鸽子就是变化的次数，一个数若变化811次，则至少有2个数是重复的，重复的一出现，后面就全一样了，就成环了。

---

 那如果是快乐数，是不是就没有环呢？其实也有，快乐数最后变为1后，若再经历一次变化还是1，其实也成环了，只是环里的元素都是1，而不是快乐数环里的元素都不是1，所以这道题目的思路很清晰了，我们只要找到一个环里元素判断是不是1就行了。

如何找到环里元素：

  面对这种环的问题，我们可以利用双指针里的快慢指针法就可以求解了，如图：

slow慢指针一次走一步，fast快指针一次走两步。

还没进环之前，slow永远无法追上fast指针，但当进环后，就像两个人在圆形跑道比赛，只要两人有速度差（速度不一样），就绝对会相遇。 只要以相遇，判断相遇时的元素是否为1就行。

代码实现：

class Solution {
public:int compute(int n)//计算n每个位上的平方和{int sum=0;while(n){int tmp = n%10;sum+=tmp*tmp;n/=10;}return sum;}bool isHappy(int n) {int slow =n,fast=compute(n);//初始fast在slow前一个while(slow!=fast){slow=compute(slow);//slow一次走一步fast=compute(compute(fast));//fast一次走两步}return fast==1;//相遇时fast或者slow等于1就是快乐数}
};