数据结构(二)——线性表(顺序表)-编程知识

二、线性表

2.1线性表的定义和基本操作

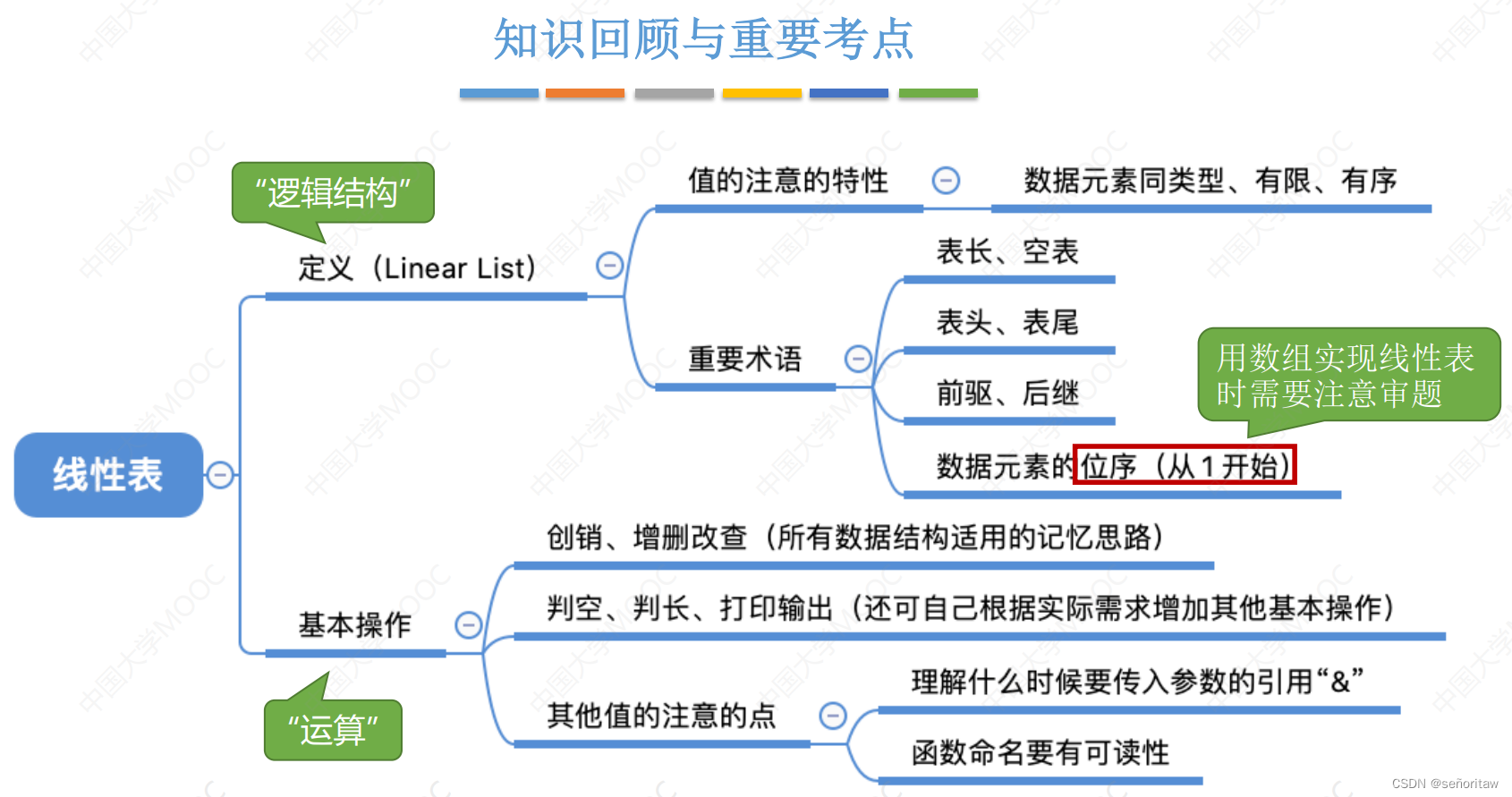
2.1.1 线性表的基本概念

线性表：是具有相同数据类型的 n 个数据元素的有限序列。
(Eg:所有的整数按递增次序排列，不是顺序表，因为所有的整数是无限的)
其中n为表长，当n=0时线性表是一个空表。若用L表示一个线性表，则

$a_{i}$ 是线性表中的第i个元素，称为线性表中的位序
$a_{1}$ 是表头元素; $a_{n}$ 是表尾元素。
除第一个元素外，每个元素有且仅有一个直接前驱;
除最后一个元素外，每个元素有且仅有一个直接后继

2.1.2 线性表的基本操作

InitList(&L)：初始化表。构造一个空的线性表 L，分配内存空间。
DestroyList(&L)：销毁操作。销毁线性表，并释放线性表 L 所占用的内存空间。
ListInsert(&L, i, &e)：插入操作。在表 L 的第 i 个位置插入指定元素 e 。
ListDelete(&L, i, &e)：删除操作。删除表 L 中第 i 个位置的元素，并用 e 返回删除元素的值。
LocateElem(L, e)：按值查找操作。在表 L 中查找具有给定关键字值的元素。
GetElem(L, i)：按位查找操作。获取表 L 中第 i 个位置的元素的值。

其他常用操作

Length(L)：求表长。返回线性表 L 的长度，即表中元素的个数。
PrintList(L)：输出操作。按前后顺序输出线性表 L 的所有元素值。
Empty(L)：判空操作。若表L 为空表，则返回 true，否则返回 false。

对数据操作的思路：创销、增删改查
什么时候要传入引用“&”—―对参数的修改结果需要“带回来”时

#include<stdio.h>void test ( int &x) {x=1024;printf ( "test函数内部x=%d\n",x) ;
}int main() {int x =1;printf( "调用test前x=d\n",x) ;test (x);printf ( "调用test后x=%din",x);
}

2.2线性表的顺序表示

2.2.1 顺序表的定义

顺序表：用顺序存储的方式实现线性表
顺序存储：把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中

C语言中通过sizeof(ElementType)可以知道一个数据元素的大小

2.2.2 顺序表的实现

静态分配

#define MaxSize 10 // 定义最大长度 typedef struct {int data[MaxSize]; // 使用静态的数组存放数据元素 int length; // 顺序表的当前长度 
}SqList;    //顺序表的类型定义//基本操作 —— 初始化一个顺序表 
void InitList(SqList &L) {for(int i=0;i<MaxSize;i++)L.data[i]=0;    //将所有数据元素设置为默认初始值L.length = 0; // 顺序表初始长度为0 
}int main() {SqList L; // 声明一个顺序表 InitList(L); // 初始化顺序表 return 0;
}

如果不设置数据元素的默认值
静态数组的表长确定后就无法更改（存储空间是静态的），最好使用动态分配

动态分配

#include <stdlib.h>    //malloc函数要使用的头文件
#define InitSize 10 // 顺序表的初始长度typedef struct {int *data; // 声明动态分配数组的指针 int MaxSize; // 顺序表的最大容量int length; // 顺序表的当前长度 
}SeqList;// 初始化顺序表 
void InitList(SeqList &L) {// 用malloc函数申请一片连续的存储空间 L.data = (int *)malloc(InitSize * sizeof(int));  //(int*)把malloc返回的指针转换成定义的同类型的指针L.length = 0;    //把数据表的长度设为0L.MaxSize = InitSize;    //把数据表的最大长度设为初始值
}// 增加动态数组的长度 
void IncreaseSize(SeqList &L, int len) {int *p = L.data;    //把顺序表的data指针的值赋给指针pL.data = (int *)malloc((L.MaxSize+len) * sizeof(int));for (int i = 0; i < L.length; i++)L.data[i] = p[i]; // 将数据复制到新区域 L.MaxSize = L.MaxSize + len; // 顺序表最大长度增加len free(p); // 释放原来的内存空间 
}int main() {SeqList L; // 声明一个顺序表 InitList(L); // 初始化顺序表 ...//往数据表中随便插入几个元素IncreaseSize(L, 5);    //再多申请5个空间return 0;
}

顺序表的特点：

随机访问，即可以在 O(1) 时间内找到第 i 个元素
存储密度高，每个节点只存储数据元素
拓展容量不方便（即使使用动态分配的方式实现，拓展长度的时间复杂度也比较高，要把数据复制到新的区域）
插入删除操作不方便，需移动大量元素

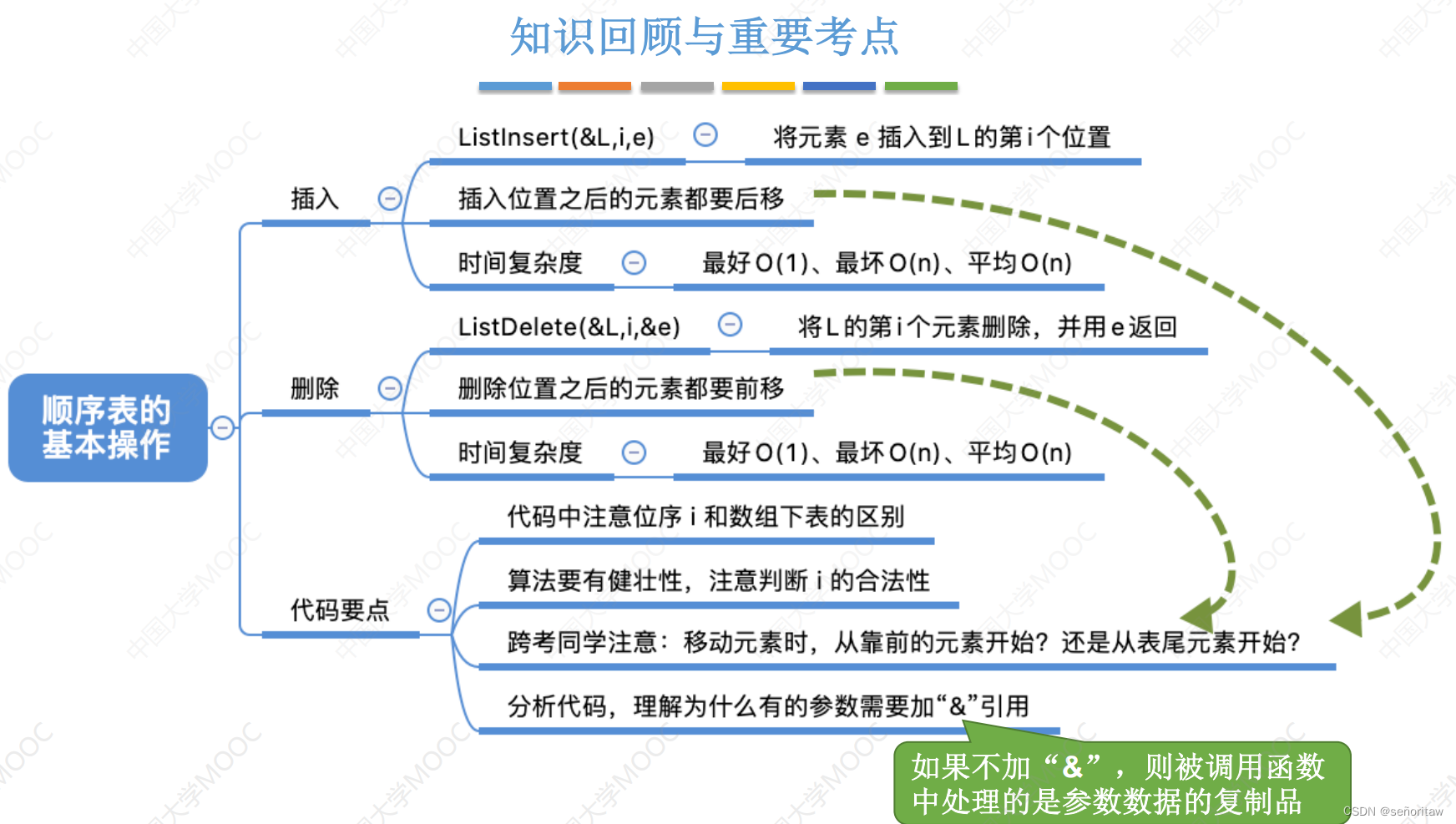
2.2.3 顺序表的插入删除

Listlnsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e

#define MaxSize 10 // 定义最大长度  10个元素typedef struct {int data[MaxSize]; // 用静态的数组存放数据元素 int length; // 顺序表的当前长度 
}SqList;    //定义数据表SqlList// 在顺序表i位置插入e
bool ListInsert(SqList &L, int i, int e) {    //注意位序、数组下标的关系 if (i < 1 || i > L.length+1) // 判断i的范围是否有效 return false;if (L.length >= MaxSize) // 判断存储空间是否已满 return false;for (int j = L.length; j >= i; j--) // 将第i个元素之后的元素后移 L.data[j] = L.data[j-1];L.data[i-1] = e; // 在位置i处放入e     i-1 下标L.length++; // 长度+1 return true;
} int main() {SqList L;    //声明一个顺序表InitList(L);    //初始化顺序表...//此次省略一些代码，插入几个元素ListInsert(L, 3, 3); //调用函数 在顺序表L的第三个位置插入数据3return 0; 
}

插入操作的时间复杂度问题规模n=L.length(表长)

最好情况：新元素插入到表尾，不需要移动元素 i = n+1，循环0次；
最好时间复杂度 = O(1)

最坏情况：新元素插入到表头，需要将原有的 n 个元素全都向后移动 i = 1，循环 n 次；
最坏时间复杂度 = O(n)

平均情况：假设新元素插入到任何一个位置的概率相同，即 i = 1,2,3, … , length+1 的概率都是 p = $\frac{1}{n+1}$ ，循环 n 次；i=2 时，循环 n-1 次；i=3，循环 n-2 次 …… i =n+1时，循环0次，平均循环次数 np + (n-1)p + (n-2)p +... + 1⋅p == $\frac{n(n+1))}{2} \frac{1}{n+1}=\frac{n}{2}$
平均时间复杂度 = O(n)

ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值。

#define MaxSize 10typedef struct {int data[MaxSize];int length;
} SqList;// 删除顺序表i位置的数据并存入e
bool ListDelete(SqList &L, int i, int &e) {    //注意e加了&引用，这里处理的e跟main函数中的e在内存中对应的是同一份数据if (i < 1 || i > L.length) // 判断i的范围是否有效return false;e = L.data[i-1]; // 将被删除的元素赋值给e for (int j = i; j < L.length; j++) //将第i个位置后的元素前移 L.data[j-1] = L.data[j];L.length--;    //线性表长度-1return true; 
}int main() {SqList L;    //声明一个顺序表InitList(L);    //初始后顺序表...//此次省略一些代码，插入几个元素int e = -1;    //用变量e把删除的元素“带回来”if (ListDelete(L, 3, e))    //调用删除操作，删除第三个位置的元素用e返回printf("已删除第3个元素，删除元素值为%d\n", e);elseprintf("位序i不合法，删除失败\n"); return 0; 
}

插入操作的时间复杂度问题规模n=L.length(表长)

最好情况：删除表尾元素，不需要移动其他元素 i = n，循环 0 次；
最好时间复杂度 = O(1)

最坏情况：删除表头元素，需要将后续的 n-1 个元素全都向前移动 i = 1，循环 n-1 次；
最坏时间复杂度 = O(n)

平均情况：假设删除任何一个元素的概率相同，即 i = 1,2,3, … , length 的概率都是 p = $\frac{1}{n}$ ，i=1时，循环 n-1 次；i=2 时，循环 n-2 次；i=3，循环 n-3 次 …… i =n时，循环0次，平均循环次数 (n-1)p + (n-2)p +... + 1⋅p == $\frac{n(n-1))}{2} \frac{1}{n}=\frac{n}{2}$
平均时间复杂度 = O(n)

2.2.4 顺序表的查找

GetElem(L,i):按位查找操作。获取表L中第i个位置的元素的值。

// 静态分配的按位查找
#define MaxSize 10    //定义最大长度typedef struct {ElemType data[MaxSize];     //用静态的数组存放元素int length;    //顺序表的当前长度
}SqList;         //顺序表的类型定义ElemType GetElem(SqList L, int i) {  //位序从1开始return L.data[i-1];    //数组下标从0开始，所以要-1
}

// 动态分配的按位查找
#define InitSize 10    //顺序表的初始长度typedef struct {ElemType *data;    //指示动态分配数组的指针  *data变量是一个指针 int MaxSize;       //顺序表的最大容量int length;        //顺序表的当前长度
}SeqList;              //顺序表的类型定义ElemType GetElem(SeqList L, int i) {return L.data[i-1];
}//*data指向了malloc分配的一整片连续空间的起始地址  即data[i-1]

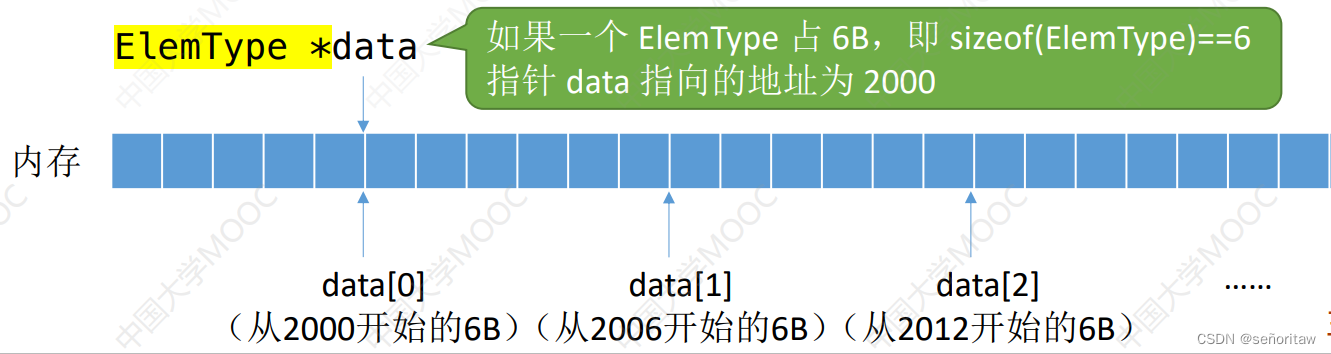
按位查找的时间复杂度 = O(1)
由于顺序表的各个数据元素在内存中连续存放，因此可以根据起始地址和数据元素大小立即找到第 i 个元素——“随机存取”特性

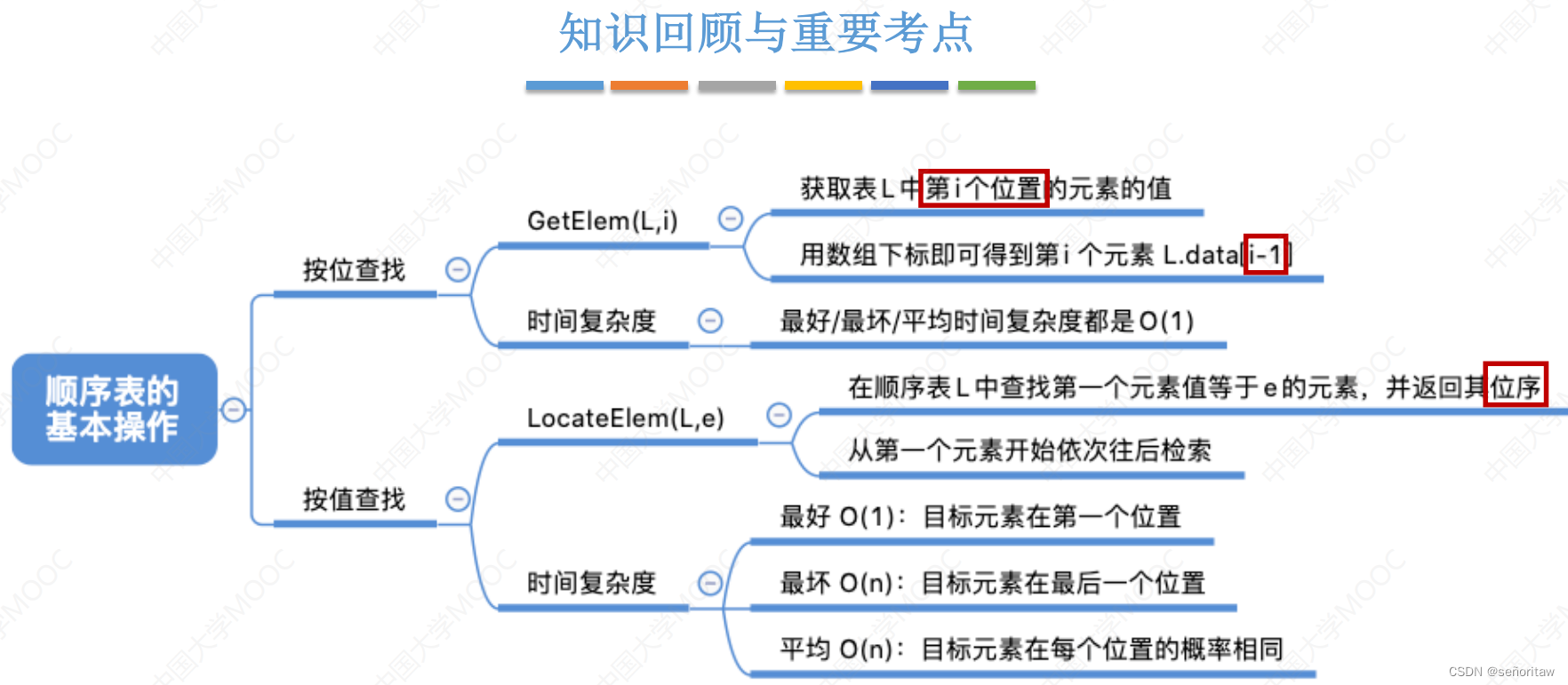
LocateElem(L,e):按值查找操作。在表L中查找具有给定关键字值的元素。

#define InitSize 10typedef struct {ElemType *data; //指示动态分配数组的指针int MaxSize;    //顺序表的最大容量    int length;     //顺序表的当前长度
}SqList;// 查找第一个元素值为e的元素，并返回其位序 
int LocateElem(SqList L, int e) {for (int i = 0; i < L.length; i++)if (L.data[i] == e)    //依次判断数据表中的数据元素跟传入的数据e是否相等return i+1; // 数组下标为i的元素值等于e，返回其位序i+1 return 0; // 没有查找到 
}

基本数据类型：int、char、double、 float 等可以直接用运算符“==”比较,结构类型的数据元素不能