介绍
wu-smart-acw-client 简称acw-client,是一个基于Lazy ORM定制的客户端代码生成小工具
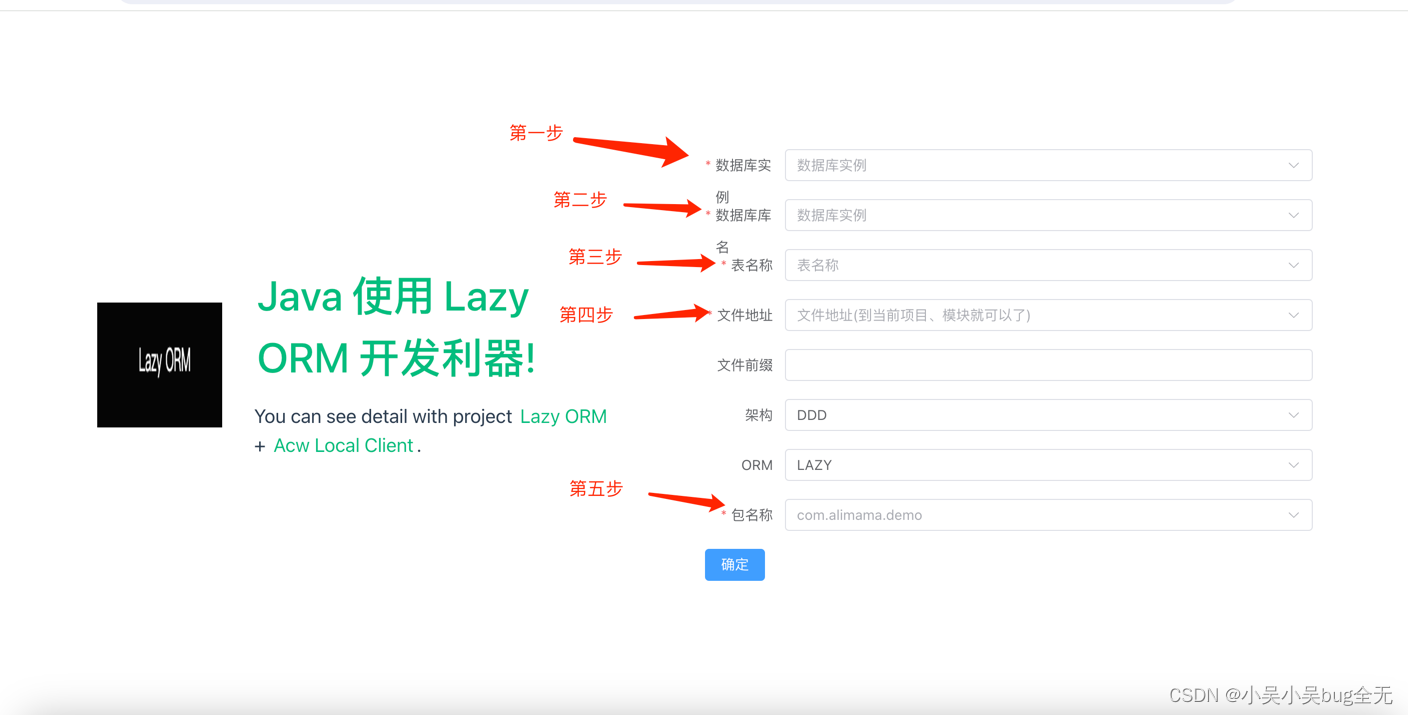
Lazy ORM 小工具 acw 本地客户端 你负责点击页面,他负责输出代码
安装
<dependency><groupId>top.wu2020</groupId><artifactId>wu-smart-acw-client</artifactId><version>1.2.2-JDK17-SNAPSHOT</version></dependency>
使用
本地只有客户端没有服务端需要配置 spring.lazy.netty.enabled: false 禁用客户端连接远程服务端
页面地址
Acw 本地客户端: http://localhost:port/acw-local-client-ui/index.html
后端框架地址
前端地址
ACW客户端使用:体验地址
效果展示