LC141环形列表(easy)

题目描述

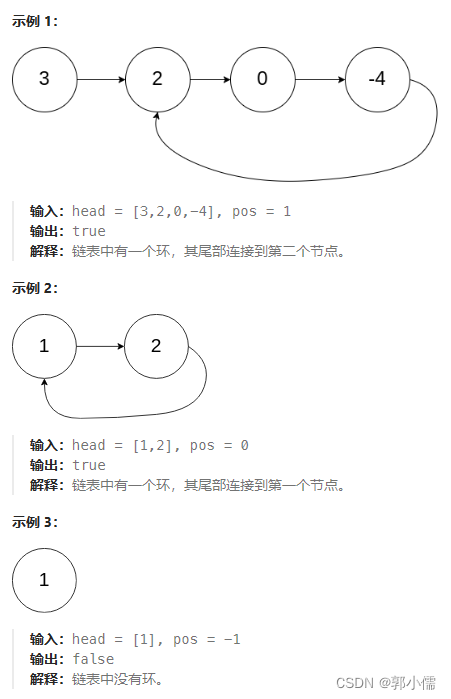
方法1：快慢指针

（1）思路

使用快慢指针特性：每轮移动之后两者的距离会加一。
当一个链表有环时，快慢指针都会陷入环中进行无限次移动，然后变成了追及问题。想象一下在操场跑步的场景，只要一直跑下去，快的总会追上慢的。

💥 如果存在环，如何判断环的长度呢？
快慢指针相遇后继续移动，直到第二次相遇。两次相遇间的移动次数即为环的长度。

（2）python代码

class Solution:def hasCycle(self, head: Optional[ListNode]) -> bool:# 快慢指针# time complexity = O(N)# space complexity = O(1)slow = headfast = head# 注意判断条件：fast, fast.next都不为None，才能循环# fast.next不为 None，也是为了使 fast.next.next 能够被定义while (fast is not None and fast.next is not None):slow = slow.nextfast = fast.next.nextif slow == fast:return Truereturn False         

（3）复杂度分析

LC881救生艇（medium）

题目描述

给定每个人的体重和救生艇的最大乘重，问需要多少条船。其中，一个船最多乘两人。

方法1：双指针-对撞指针

（1）思路

为什么会想到对撞指针？
对撞指针就很适合需要把一串数的两个加起来，判断是否小于一个数的情况（LC1两数之和）
对撞指针的特性就是：一定要先排序（time complexity= o(nlogn）

（2）Python代码

class Solution:def numRescueBoats(self, people: List[int], limit: int) -> int:# 双指针——对撞指针# time complexity = o(nlogn)# space complexity = o(1)people.sort() # first step 一定是排序 time complexity = o(nlogn)n = len(people)    if people is None and n == 0: # 考虑没有人的情况return 0 left = 0right = n - 1ship = 0while left <= right: # 对撞指针时间复杂度是o(n)if people[left] + people[right] <= limit:left+= 1right -= 1ship += 1return ship

（3）复杂度分析

time complexity = $O(nlogn)$ 主要是排序的时间复杂度
space complexity = $O(1)$ 只用了两个指针

LC11成最多水的容器 medium

1. 题目描述

给一组数据height，代表一列高，需要做的是，从中找出两个，和x周共同构成容器，可以容纳更多的水。

输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49

方法：双指针

（1）思路

核心思想：短板决定容器的高度，要移动短板

（2）python代码

class Solution:def maxArea(self, height: List[int]) -> int:# time complexity = o(n) 双指针需要遍历一遍底边长度也就是height的大小n# space complexity = o(1) 使用的都是常数，没有新建数组n = len(height)left,right = 0,n-1max_water = 0while left < right:h = min(height[left],height[right]) # 短板的长度才是真正的高a = right - lefts = a * hmax_water = max(max_water,s)# 舍去短板if height[left] <= height[right]:left += 1else:right -=1return max_water

（3）复杂度分析

时间复杂度：$O(n)$：双指针需要遍历一遍底边长度也就是height的大小n
空间复杂度：$O(1)$：使用的都是常数，没有新建数组

LC704二分查找 easy

题目描述

给定一个长度为$n$的数组 nums ，元素按从小到大的顺序排列且不重复。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素，则返回-1。

方法：二分查找法

###（1）思路





流程：

（2）python代码

def binary_search(nums: list[int], target: int) -> int:"""二分查找（双闭区间）"""# 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素i, j = 0, len(nums) - 1# 循环，当搜索区间为空时跳出（当 i > j 时为空）while i <= j:# 理论上 Python 的数字可以无限大（取决于内存大小），无须考虑大数越界问题m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # 此情况说明 target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1  # 此情况说明 target 在区间 [i, m-1] 中else:return m  # 找到目标元素，返回其索引return -1  # 未找到目标元素，返回 -1

（3）复杂度分析

时间复杂度：$O(logn)$每次循环区间减少一半，因此循环次数是$O(logn)$
空间复杂度：$O(1)$没用使用数组啥的

（4）说明

上述这种方法是是双闭区间的类型（$i=0,j=n-1$），二分查找还有左闭右开区间（$i=0,j=n$）,这种情况下，当$i==j$时，区间$[i,j)$为空
左闭右开区间的Python代码：

def binary_search_lcro(nums: list[int], target: int) -> int:"""二分查找（左闭右开区间）"""# 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1i, j = 0, len(nums)# 循环，当搜索区间为空时跳出（当 i = j 时为空）while i < j:m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # 此情况说明 target 在区间 [m+1, j) 中elif nums[m] > target:j = m  # 此情况说明 target 在区间 [i, m) 中else:return m  # 找到目标元素，返回其索引return -1  # 未找到目标元素，返回 -1

LC35 搜索插入位置 easy （二分查找法变种问题）

问题描述

LC704：给定一个长度为$n$的数组 nums ，元素按从小到大的顺序排列且不重复。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素，则返回-1。

LC35：给定一个长度为$n$的数组 nums ，元素按从小到大的顺序排列且不重复。给一个元素target，想要插入到nums中，并保持有序性。如果数组中存在target，就将targat插入到左侧；如果不存在，将target插入到按顺序插入的位置，返回索引。

方法：二分查找

（1）思路

⭐️思考：
Q1： 当数组中有target的时候，插入点的索引是否就是返回值？
回答： yep！当查找到原数组有target值时，新的target要放在老的target的左侧，也就是说新的target代替了老的target的位置，也就是插入点的索引就是新插入的target的索引
**Q2：**当数组不存在target的时候，新插入点是哪个元素的索引？

剩下思路和二分查找一致

（2）python

def binary_search_insertion_simple(nums: list[int], target: int) -> int:"""二分查找插入点（无重复元素）闭区间"""i, j = 0, len(nums) - 1  # 初始化双闭区间 [0, n-1]while i <= j:m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1  # target 在区间 [i, m-1] 中else:return m  # 找到 target ，返回插入点 m# 未找到 target ，返回插入点 ireturn i