Floyd算法：浅显外表下的动态规划内核-编程知识

很久没遇到Floyd算法的题目了，2642. 设计可以求最短路径的图类刚好是一个典型。在实现核心算法之余，顺便整理一下算法的内核。

Floyd-Warshall’s Algorithm

Floyd-Warshall算法，简称Floyd算法，是“有向图非负权图的多源最短路”的经典算法和通用解法，以极其精炼的代码著称：

let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
for each edge (u, v) dodist[u][v] ← w(u, v)  // The weight of the edge (u, v)
for each vertex v dodist[v][v] ← 0
for k from 1 to |V|for i from 1 to |V|for j from 1 to |V|if dist[i][j] > dist[i][k] + dist[k][j] dist[i][j] ← dist[i][k] + dist[k][j]end if

算法核心的三层循环，最外层的k，作为串联首位节点i、j的中间节点，其必须位于最外层，否则算法的正确性就遭到了破坏。由于整个迭代的主次序是由k决定的，就好像将中间节点一个一个地“插入”进来，所以Floyd算法又被称为“插点法”。这个不能随意改变次序的三层循环，实际上正是“动态规划”所严格强调的“子状态”和“顺序”的核心体现。

插点法与动态规划

从伪码上看，我们的整个动态规划的状态转移似乎是：
$\displaystyle \mathrm {dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])}$
但如果任意翻一本教科书，会找到的其实是另一种形式的转移方程：
$\displaystyle \mathrm { dist[i][j][k] = min(dist[i][j][k-1], dist[i][k][k-1] + dist[k][j][k-1])}$
我们发现第三个维度被大多数写法有意无意地隐藏掉了，这其实是很常见的优化手段。但如果没看过原始版本的转移方程，就很容易误认为只有两个维度，迭代顺序也可以调换。那怎么理解这个原始转移方程呢？dist[i][j][k]实际上代表的是，我们定义一个中间节点集合S = {0, 1, 2, ..., k-1}，让这k个点以任意顺序组合插入到i和j之间时，从i到j的最短路径长度；不失一般性，k = 0表示中间节点为空集合，那么dist[i][j][0]就是直接从i出发到j的边的长度。所以迭代过程中，我们实际上一个一个地将节点加入到集合S中，所以这个顺序是不能调换的。注意，我们说到中间节点的任意组合，实际上意味着多少种组合呢？能否理解好这点，决定了我们能不能彻底看清Floyd算法的本质。

插点与最短路

为了理解插点法的魅力，我们先来思考一下我们在处理的问题是一个怎样规模的系统。首先，在有向图里，我们能有多少条不重复的边呢？如果节点数为n，我们从每个节点出发，都能到达另外的n-1个节点，所以边的数量最多为n(n-1)。那么，我们能构成多少条不同的路径呢？有一个直觉是，如果不对这个问题加一个限定，它将导向+∞。

因为这样的“富边图”里一定有环，只要有环，路径数就是无穷多的。但是我们可以很简单地加一个限定，就是找一找不经过重复节点的路径数量。因此，从i到j的不经过重复节点的路径数量是另外n-2个节点的全排列组合的总和：

$\displaystyle \mathrm{C_{n-2}^{n-2}(n-2)! + C_{n-2}^{n-3}(n-3)! + ... + C_{n-2}^{0} = \sum_{k=0}^{n-2} C_{n-2}^{k}k!}$

其中k同前文所述，代表我们引入了k个插点。我们简单放大一下，发现单源情况下路径数量应该是(n-1)!级别：

$\displaystyle \mathrm{ \sum_{k=0}^{n-2} C_{n-2}^{k}k! ≤ (n-1)(n-2)! = (n-1)!}$

如果再枚举一下起点和终点，整个“多源最短路问题”的复杂度是 $\displaystyle \mathrm {O(n!)}$ 级别，甚至大于指数级。那么Floyd算法能在多项式时间 $\displaystyle \mathrm {O(n^3)}$ 内，完成对该问题的解答，并且还如此精炼，无疑是动态规划的强大魔力。此外，我们仔细检查上面这些路径也恰恰是“最短路”的备选路径，因为我们可以简单用反证法证明，在路径中引入任意一个重复节点，都必然存在比其更优的路径。
在这里插入图片描述
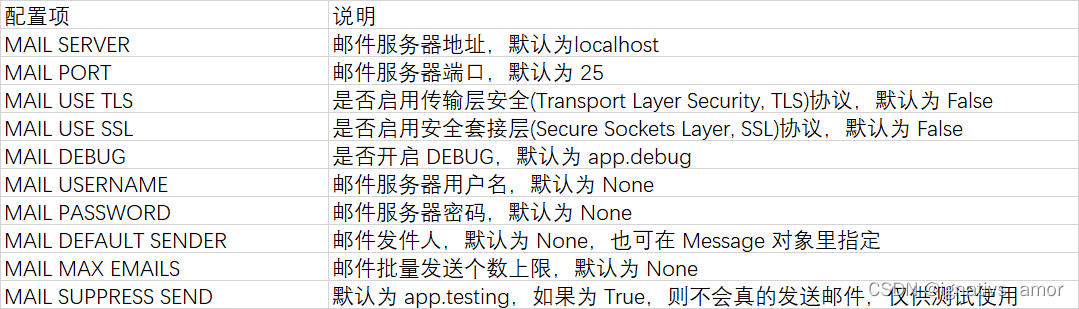
如上图所示，如果路径中存在重复的中间节点，因为图里没有负权边，所以上面三条路径E1、E2、E3一定都大于等于0，那么必然有：
$\displaystyle \mathrm { E1 + E3 <= E1 + E2 + E3}$
则我们必然可以通过精简掉E2这段路达到一个相对更短的路径，所以存在重复节点的路径必然不是最短路。

拆解插点法

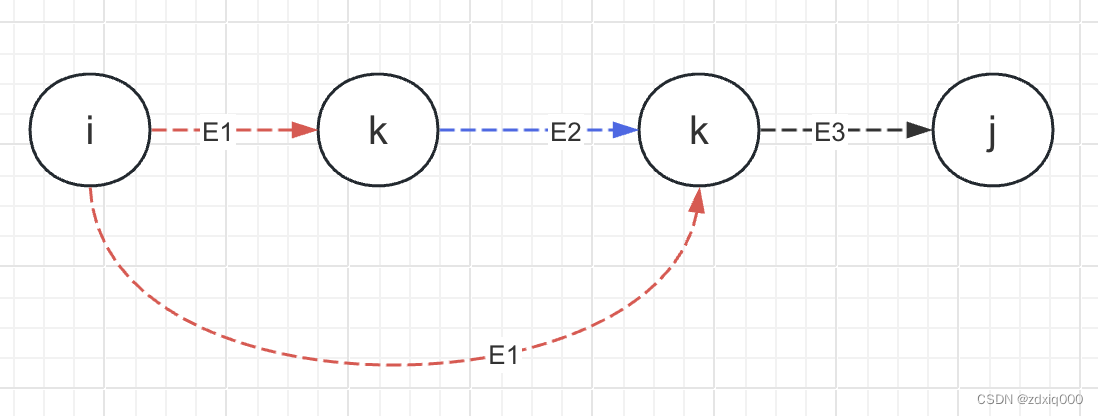
现在我们回到插点法本身，继续讨论插点集合S和路径数量之间的关系。通过前面的分析，我们已经知道这个路径数量随着插点的增加是阶乘级别地上升，但刚开始还是相当温和的，比如在不插入点和只插入一个点时，总共的路径也就两条：
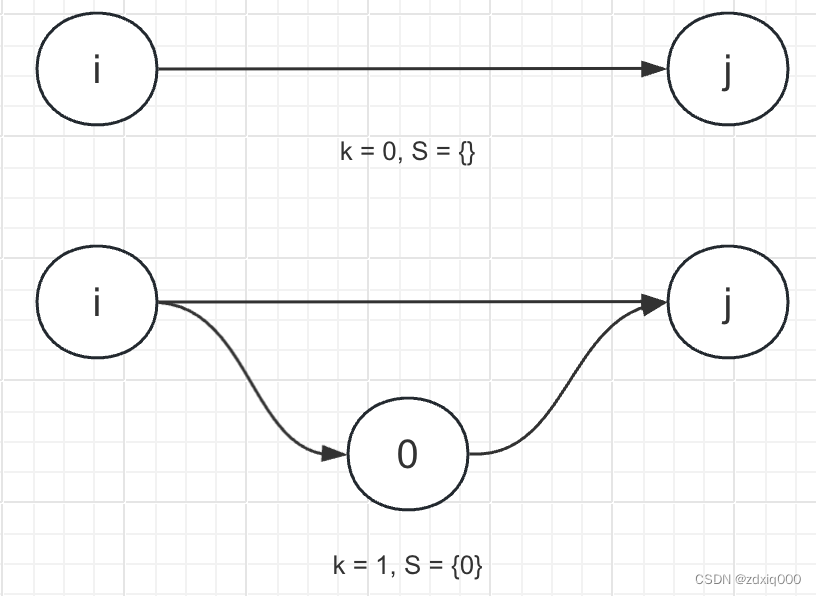
在这里插入图片描述

那么，当k=2时，又如何呢？我们发现路径开始快速膨胀。
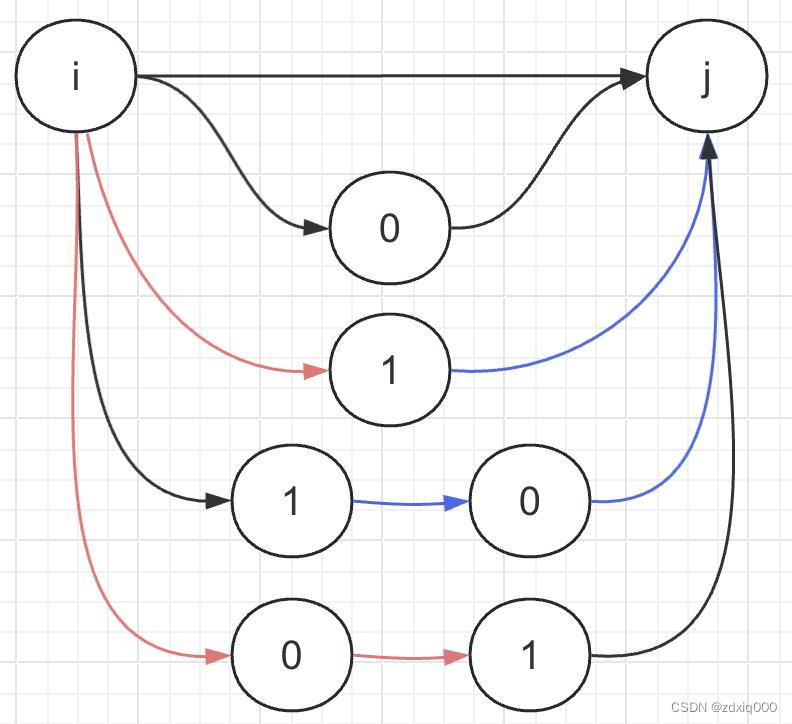
在这里插入图片描述
这里面我们发现通过一次状态转移，我们同时继承了插入一个以下节点的所有结果——例如，蓝色的路径其实是1到j目前（插一点）所有的备选路径、红色路径其实是i到0目前所有的备选路径。这些备选路径中的最短值，其实已经计算过了并且存储在 $\displaystyle \mathrm{dist[i][1]}$ 和 $\displaystyle \mathrm{dist[1][j]}$ 之中了，上面的图就是已经计算过的“路径的任意组合”，而所有最优、最短路径的再组合，就是Floyd算法动态规划中状态转移的实质。因此，在没有计算完所有插k-1点的组合之前，我们是绝对不可能计算插k点的最短路的。