前缀和
前缀和的作用: 快速求出元素组中某段区间的和
为什么下标要从1 开始:为了方便后面的计算,避免下标转换,设为零,不影响结果
- 定义两个数组,第一个为原始数组(a[]),第二个为前缀和数组(s[])
前缀和的计算 s[i] = s[i-1]+a[i]
int[] s = new int[x];
for (int i = 1; i <=n ; i++) {s[i] = s[i-1]+arr[i];
}
区间的和
s[r]-s[l-1]的结果就是所求区间的和
二维数组的前缀和问题
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + arr[i][j]
输入区间范围(x1,y1,x2,y2),s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]的结果就是所求区间的和
差分问题
差分的作用:如果对某个区间需要每个元素加上C则需要使用差分来减少时间复杂度。
差分的重点是:构造临时数组b[]
两个数组:a[],b[],a[]称为b[]的前缀和,b[]称为a[]的差分
void insert(int l,int r,int c){b[l] +=c;b[r+1] -=c;
}
//构造差分数组
for (int i = 1; i <=n ; i++) {b[i] = a[i]-a[i-1];
}
//插入方法:假设a[]中全部为0 则b[]也全部为0,可以执行插入操作
for(int i = 1; i <= n; i++){insert(i,i,a[i])
}- 将所求区间(l,r)在b[]数组划分出来并加上c,公式:b[l] +=c,b[r+1] -=c;
将差分数组转换成原数组,也就是求差分数组的前缀和,公式:a[i] = a[i-1] +b[i] //类比于s[i]=s[i-1]+a[i]
for (int i = 1; i <=n ; i++) {a[i] = a[i-1]+b[i];System.out.print(a[i]+" ");
}
二维数组的差分
b[][]是a[][]的差分数组
public static void insert(int x1,int y1,int x2,int y2,int c){b[x1][y1] += c;b[x2+1][y1] -=c;b[x1][y2+1] -=c;b[x2+1][y2+1] +=c;
}
初始化原数组a[][]
for (int i = 1; i <=n; i++) {
for (int j = 1; j <=m ; j++) {
a[i][j] = sc.nextInt();
}
}
构造差分数组
初始化B数组从[1][1]到[i][j]添加元素,就是将a[][]中的元素遍历到B数组中
int[][] b = new int[x][x];
for (int i = 1; i <=n; i++) {
for (int j = 1; j <=m ; j++) {
insert(i,j,i,j,a[i][j]);
}
}
输入矩形中需要+c的范围(x1,y1)(x2,y2),在差分数组b[][]中找到相应的范围+c
while (q-- != 0){int x1,y1,x2,y2;x1 = sc.nextInt();y1 = sc.nextInt();x2 = sc.nextInt();y2 = sc.nextInt();int c = sc.nextInt();insert(x1,y1,x2,y2,c);
}
求b[][]数组中的前缀和-->a[][];公式:b[i][j]=a[i][j]−a[i−1][j]−a[i][j−1]+a[i−1][j−1]
for (int i = 1; i <=n ; i++) {for (int j = 1; j <=m ; j++) {b[i][j] = b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1] + b[i][j];System.out.print(b[i][j]+" ");}
}直接输出b[][]中的元素就是a[][]数组中范围所需要+c的结果

#include <bits/stdc++.h>
// 2024-04-01 Come on !
using namespace std;
#define ll long long
const int N =1e5+10;
ll n,m,x,y,z;
ll a[N],D[N];int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // no endll; while(cin>>n>>m){for(int i=1;i<=n;i++){cin>>a[i];//TODOD[i]=a[i]-a[i-1];}while(m--){cin>>x>>y>>z;D[x]+=z;D[y+1]-=z;}//更新恢复for(int i=1;i<=n;i++){a[i]=a[i-1]+D[i];//TODOcout<<a[i]<<" ";}cout<<"\n";}return 0;
}
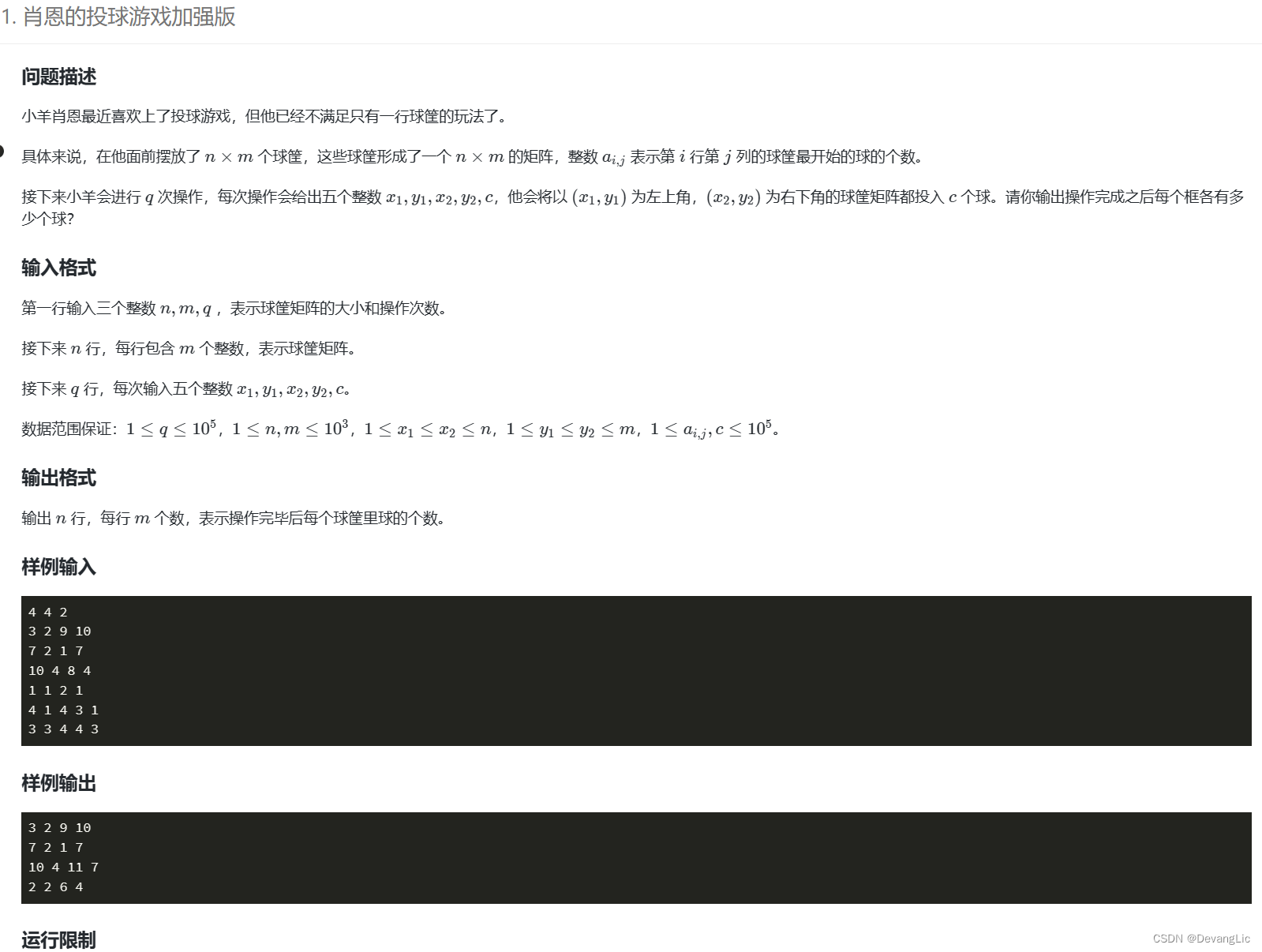
practice 二维差分
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1010;
ll a[N][N], b[N][N];int main() {int n, m, q; cin >> n >> m >> q;for(int i = 1; i <= n; ++ i)for(int j = 1; j <= m; ++ j) cin >> a[i][j];while(q -- ) {int x1, y1, x2, y2, c; cin >> x1 >> y1 >> x2 >> y2 >> c;b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;}for(int i = 1; i <= n; ++ i)for(int j = 1; j <= m; ++ j) {b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];a[i][j] += b[i][j];cout << a[i][j] << " " << " \n"[j == m];}return 0;
}