知识点
1. 求二进制中1的个数
int get_count(int x)//返回x的二进制有多少个1
int get_count(int x)
{int res = 0;while (x){res ++ ;x -= x & -x;}return res;
}
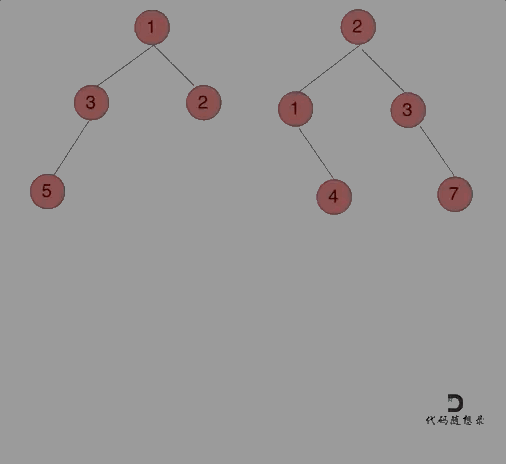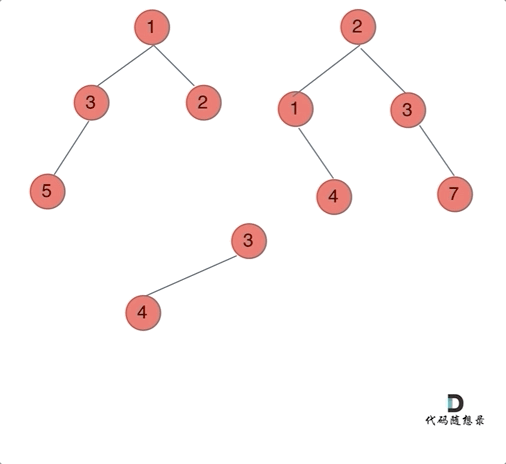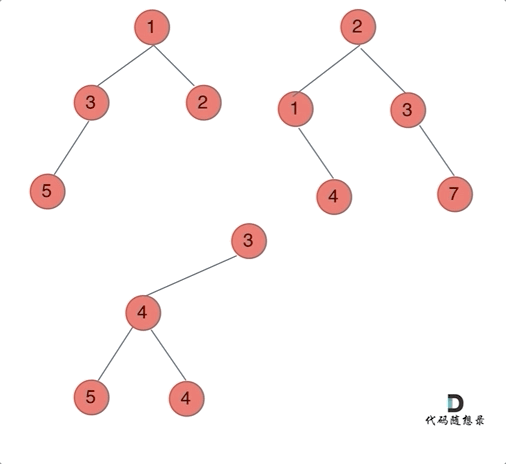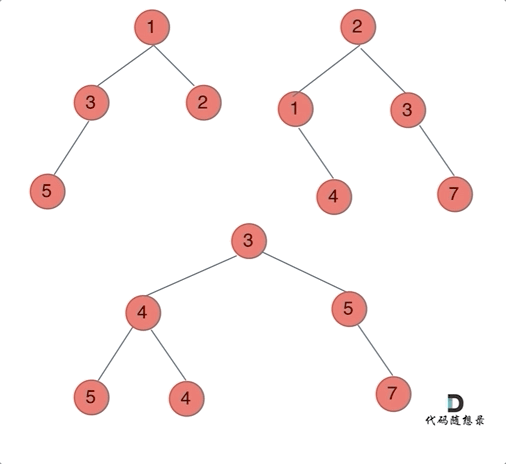
2. 建树,和树的DFS
记得初始化头节点
const int N = 1e5 + 10, M = N * 2;
int h[N], e[M], ne[M], idx;void add(int a, int b) //如果是无向图,加两条边
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}int dfs(int u)
{state[u] = true;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(!state[j])dfs(j);}
}
3. 快速幂 O(logk)
用来快速求出ak mod p的结果
数据范围: 1 <= a, p, k <= 109
//两个十的九次方数相乘会爆int
typedef long long LL;
int qmi(int a, int k, int p)
{int res = 1;while(k){if(k & 1) res = (LL)res * a % p; //要先转型再计算k >>= 1;a = (LL)a * a % p;}return res;
}
4. 分解质因数 O(sqrt(n))
void divide(int x)
{for(int i = 2; i * i <= n; i++)if(x % i == 0){int s = 0;while(x % i == 0) x /= i, s++;cout << i << " " << s << endl;}//大于根号x的数只能有一个,此时x也是质因子if(x > 1) cout << x << " " << 1 << endl; cout << endl;
}
5. 欧拉函数

int phi(int x)
{int res = x;for(int i = 2; i * i <= n; i++)if(x % i == 0){while(x % i == 0) x /= i;res = res / i * (i - 1);}if(x > 1) res = res / x * ( x - 1 );return res;
}
6. 最大公约数 O(n(log(n))
//辗转相除法
int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}
//辗转相减法