【算法详解】二分查找-编程知识

1. 二分查找算法介绍

「二分查找算法（Binary Search Algorithm）」：也叫做 「折半查找算法」、「对数查找算法」。是一种在有序数组中查找某一特定元素的搜索算法。

基本算法思想：先确定待查找元素所在的区间范围，在逐步缩小范围，直到找到元素或找不到该元素为止。

二分查找算法的过程如下所示：

每次查找时从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；
如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。
如果在某一步骤数组为空，则代表找不到。

举个例子来说，给定一个有序数组 [0, 1, 2, 3, 4, 5, 6, 7, 8]。如果我们希望查找 5 是否在这个数组中。

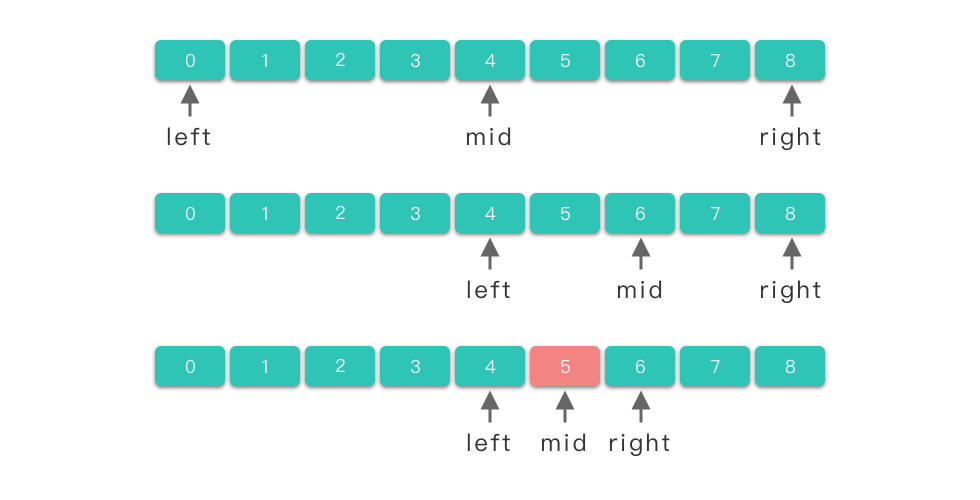
第一次区间为整个数组 [0, 1, 2, 3, 4, 5, 6, 7, 8]，中位数是 4，因为 4 小于 5，所以如果 5 存在在这个数组中，那么 5 一定在 4 右边的这一半区间中。于是我们的查找范围变成了 [4, 5, 6, 7, 8]。
第二次区间为 [4, 5, 6, 7, 8]，中位数是 6，因为 5 小于 6，所以如果 5 存在在这个数组中，那么 5 一定在 6 左边的这一半区间中。于是我们的查找范围变成了 [4, 5, 6]。
第三次区间为 [4, 5, 6]，中位数是 5，正好是我们需要查找的数字。

于是我们发现，对于一个长度为 9 的有序数组，我们只进行了 3 次查找就找到了我们需要查找的数字。而如果是按顺序依次遍历数组，则最坏情况下，我们需要查找 9 次。

二分查找过程的示意图如下所示：

2. 二分查找算法思想

二分查找算法是经典的 「减而治之」 的思想。

这里的 「减」 是减少问题规模的意思，「治」 是解决问题的意思。「减」 和 「治」 结合起来的意思就是 「排除法解决问题」。即：每一次查找，排除掉一定不存在目标元素的区间，在剩下可能存在目标元素的区间中继续查找。

每一次通过一些条件判断，将待搜索的区间逐渐缩小，以达到「减少问题规模」的目的。而于问题的规模是有限的，经过有限次的查找，最终会查找到目标元素或者查找失败。

3. 查找的三种常见模板

3.1模板I

模板I是二分查找的基础模板，适用于可以通过访问数组中单个索引来确定元素或条件的情况。关键属性包括：

查找条件可以在不与元素的两侧进行比较的情况下确定。
不需要后处理，每一步都在检查是否找到了元素。

int binarySearch(vector<int>& nums, int target) {if (nums.size() == 0) return -1;int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) return mid;else if (nums[mid] < target) left = mid + 1;else right = mid - 1;}return -1;
}

3.2模板II

模板II是二分查找的高级模板，适用于需要访问数组中当前索引及其直接右邻居索引的情况。关键属性包括：

查找条件需要访问元素的直接右邻居。
使用元素的右邻居来确定是否满足条件，并决定是向左还是向右。
保证查找空间在每一步中至少有2个元素。
需要进行后处理，当剩下1个元素时，需要评估剩余元素是否符合条件。

int binarySearch(vector<int>& nums, int target) {if (nums.size() == 0) return -1;int left = 0, right = nums.size();while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] == target) return mid;else if (nums[mid] < target) left = mid + 1;else right = mid;}if (left != nums.size() && nums[left] == target) return left;return -1;
}

3.3 模板III

模板III是二分查找的另一种形式，适用于搜索需要访问当前索引及其在数组中的直接左右邻居索引的情况。关键属性包括：

搜索条件需要访问元素的直接左右邻居。
使用元素的邻居来确定是向右还是向左。
保证查找空间在每个步骤中至少有3个元素。
需要进行后处理，当剩下2个元素时，需要评估其余元素是否符合条件。

int binarySearch(vector<int>& nums, int target) {if (nums.size() == 0) return -1;int left = 0, right = nums.size() - 1;while (left + 1 < right) {int mid = left + (right - left) / 2;if (nums[mid] == target) return mid;else if (nums[mid] < target) left = mid;else right = mid;}if (nums[left] == target) return left;if (nums[right] == target) return right;return -1;
}

4 题目描述

给定一个按照升序排列的长度为n的整数数组，以及 q 个查询。对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。如果数组中不存在该元素，则返回“-1 -1”。

输入格式

第一行包含整数n和q，表示数组长度和询问个数。
第二行包含n个整数（均在1~10000范围内），表示完整数组。
接下来q行，每行包含一个整数k，表示一个询问元素。

输出格式

共q行，每行包含两个整数，表示所求元素的起始位置和终止位置。如果数组中不存在该元素，则返回“-1 -1”。

数据范围

1 ≤ n ≤ 100000
1 ≤ q ≤ 10000
1 ≤ k ≤ 10000

输入样例

6 3
1 2 2 3 3 4
3
4
5

输出样例

3 4
5 5
-1 -1

题解思路

这道题可以使用二分查找来解决。我们首先实现两个二分查找函数，一个用于找到元素k的起始位置，另一个用于找到元素k的终止位置。然后，对于每个查询，我们使用这两个函数分别找到起始位置和终止位置，并输出结果。

参考代码

#include<iostream>
using namespace std;int n, q;
const int N = 100010;
int a[N];int binary_search(int k) {int l = 0, r = n - 1;while (l < r) {int mid = l + r >> 1;if (a[mid] < k) l = mid + 1;else r = mid;}return l;
}int binary_search2(int k) {int l = 0, r = n - 1;while (l < r) {int mid = l + r + 1 >> 1;if (a[mid] > k) r = mid - 1;else l = mid;}return l;
}int main() {scanf("%d%d", &n, &q);for (int i = 0; i < n; i++)scanf("%d", &a[i]);while (q--) {int temp;scanf("%d", &temp);int p = binary_search(temp);int q = binary_search2(temp);if (a[p] == temp)cout << p << " " << q << endl;else cout << "-1 -1" << endl;}return 0;
}