Qt判断一个点在多边形内还是外（支持凸边形和凹变形）-编程知识

Qt判断一个点在多边形内还是外（支持凸边形和凹变形）_qt 判断点是否在多边形内-CSDN博客

这里实现的方法是转载于https://blog.csdn.net/trj14/article/details/43190653和https://blog.csdn.net/WilliamSun0122/article/details/77994526
来实现的，并且按照Qt的规则进行了调整。
以下实现方法有四种，每种方法的具体讲解在转载的博客中有说明，这里不做重复阐述。
这里只说下代码的具体实现和每种方法的时间复杂度。

强烈推荐第一种方法，其它三种针对一些特殊图形或多或少都有一些问题。

方法一：射线法

时间复杂度：O(n) 。
适用范围：任意多边形。
优点：不需考虑精度误差和多边形点给出的顺序。
算法思想：以被测点Q为端点，向任意方向作射线（一般水平向右作射线），统计该射线与多边形的交点数。如果为奇数，Q在多边形内；如果为偶数，Q在多边形外。计数的时候会有一些特殊情况，如图

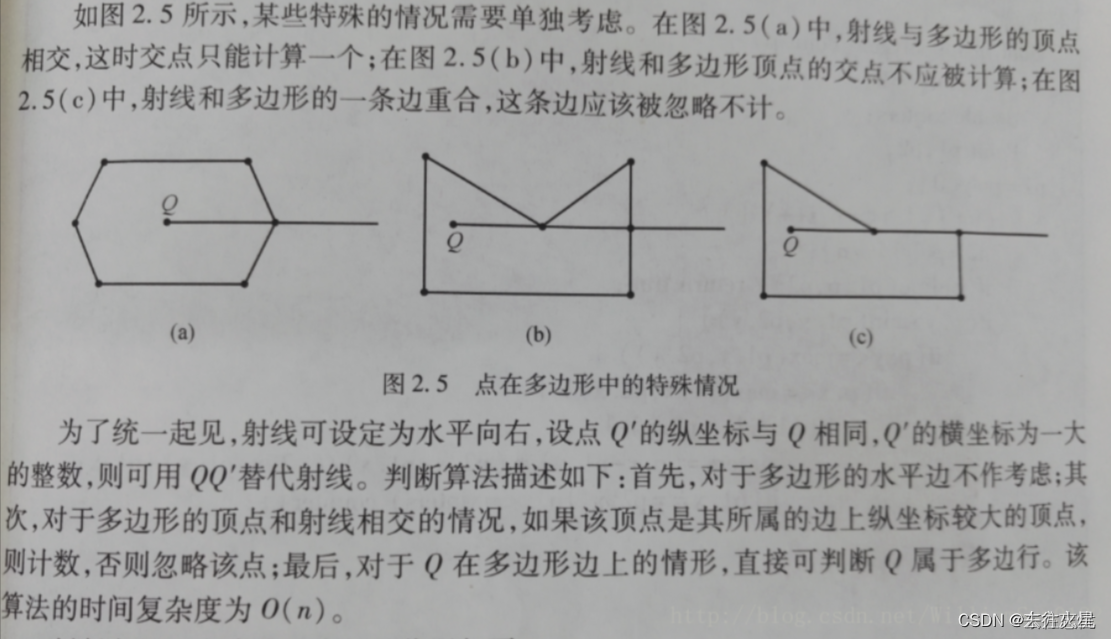
//判断点P在多边形内-射线法
bool Widget::InsidePolygon( QVector<QPointF> polygon,QPointF pt )
{int i,j;bool inside,redo;int N = polygon.size();redo = true;for (i = 0;i < N;++i){// 是否在顶点上if (polygon[i].x() == pt.x() && polygon[i].y() == pt.y()){redo = false;inside = true;break;}}while (redo){redo = false;inside = false;for (i = 0,j = N - 1;i < N;j = i++){if ( (polygon[i].y() < pt.y() && pt.y() < polygon[j].y()) ||(polygon[j].y() < pt.y() && pt.y() < polygon[i].y()) ){if (pt.x() <= polygon[i].x() || pt.x() <= polygon[j].x()){double _x = (pt.y()-polygon[i].y())*(polygon[j].x()-polygon[i].x())/(polygon[j].y()-polygon[i].y())+polygon[i].x();if (pt.x() < _x)          // 在线的左侧inside = !inside;else if (pt.x() == _x)    // 在线上{inside = true;break;}}}else if ( pt.y() == polygon[i].y()){if (pt.x() < polygon[i].x())    // 交点在顶点上{if (polygon[i].y() > polygon[j].y())pt.setY(pt.y() - 1);elsept.setY(pt.y() + 1);redo = true;break;}}else if ( polygon[i].y() ==  polygon[j].y() && pt.y() == polygon[i].y() &&((polygon[i].x() < pt.x() && pt.x() < polygon[j].x()) ||(polygon[j].x() < pt.x() && pt.x() < polygon[i].x())) )// 在水平的边界线上{inside = true;break;}}}return inside;
}

方法二：面积和判别法

时间复杂度：大于O(n)。
适用范围：所有凸边形，部分凹变形。
优点：算法简单。
缺点：有精度要求，强调多边形点给出的方向（逆时针）。
算法思想：如果点在多边形内部或者边上，那么点与多边形所有边组成的三角形面积和等于多边形面积。多边形的面积可以用叉积计算即连接坐标原点和各顶点形成向量，所有向量叉积的0.5的和即为多边形面积。不过计算面积是会有一定误差的，需要设置精度的误差范围。

//面积和判别法
bool InsidePolygon3( QVector<QPointF> polygon,QPointF pt )
{int i,j;bool inside = false;double polygon_area = 0;double trigon_area = 0;int N = polygon.size();for (i = 0,j = N - 1;i < N;j = i++){polygon_area += polygon[i].x() * polygon[j].y() - polygon[j].x() * polygon[i].y();trigon_area += abs(pt.x() * polygon[i].y() -pt.x() * polygon[j].y() -polygon[i].x() * pt.y() +polygon[i].x() * polygon[j].y() +polygon[j].x() * pt.y() -polygon[j].x() * polygon[i].y());}trigon_area *= 0.5;polygon_area = abs(polygon_area * 0.5);if ( fabs(trigon_area - polygon_area) < 1e-7 )inside = true;return inside;
}

方法三：点线判别法

时间复杂度：O(n)。
适用范围：所有凸边形，部分凹变形。
算法思想：对于多边形（正向，即逆时针），如果一个点它的所有有向边的左边，那么这个点一定在多边形内部。利用叉积正好可以判断点与给定边的关系，即点是在边的左边右边还是边上。

//点线判别法
bool InsidePolygon4( QVector<QPointF> polygon,QPointF p )
{int i,j;bool inside = false;int count1 = 0;int count2 = 0;int N = polygon.size();for (i = 0,j = N - 1;i < N;j = i++){double value = (p.x() - polygon[j].x()) * (polygon[i].y() - polygon[j].y()) - (p.y() - polygon[j].y()) * (polygon[i].x() - polygon[j].x());if (value > 0)++count1;else if (value < 0)++count2;}if (0 == count1 ||0 == count2){inside = true;}return inside;
}

方法四：角度和判别法

时间复杂度：O(n)。
适用范围：所有凸边形，部分凹变形。
优点：不强调多边形点给出顺序。
缺点：这个算法对精度的要求很高（会造成很大精度误差）。
算法思想：连接被测点与多边形所有顶点所形成的所有角的角度和在精度范围内等于则该点在多边形内，否则在多边形外。

// 根据需要不判断顶点
bool IsPointInLine( QPointF &pt,QPointF &pt1,QPointF &pt2 )
{bool inside = false;if (pt.y() == pt1.y() &&pt1.y() == pt2.y() &&((pt1.x() < pt.x() && pt.x() < pt2.x()) ||(pt2.x() < pt.x() && pt.x() < pt1.x())) ){inside = true;}else if (pt.x() == pt1.x() &&pt1.x() == pt2.x() &&((pt1.y() < pt.y() && pt.y() < pt2.y()) ||(pt2.y() < pt.y() && pt.y() < pt1.y())) ){inside = true;}else if ( ((pt1.y() < pt.y() && pt.y() < pt2.y()) ||(pt2.y() < pt.y() && pt.y() < pt1.y())) &&((pt1.x() < pt.x() && pt.x() < pt2.x()) ||(pt2.x() < pt.x() && pt.x() < pt1.x())) ){if (0 == (pt.y()-pt1.y())/(pt2.y()-pt1.y())-(pt.x() - pt1.x()) / (pt2.x()-pt1.x())){inside = true;}}return inside;
}//角度和判别法
bool InsidePolygon2( QVector<QPointF> polygon,QPointF p)
{int i,j;double angle = 0;bool inside = false;int N = polygon.size();for (i = 0,j = N - 1;i < N;j = i++){if (polygon[i].x() == p.x() &&    // 是否在顶点上polygon[i].y() == p.y()){inside = true;break;}else if (IsPointInLine(p,polygon[i],polygon[j]))    // 是否在边界线上{inside = true;break;}double x1,y1,x2,y2;x1 = polygon[i].x() - p.x();y1 = polygon[i].y() - p.y();x2 = polygon[j].x() - p.x();y2 = polygon[j].y() - p.y();double radian = atan2(y1,x1) - atan2(y2,x2);radian = abs(radian);if (radian > M_PI) radian = 2* M_PI - radian;angle += radian;            // 计算角度和}if ( fabs(6.28318530717958647692 - angle) < 1e-7 )inside = true;return inside;
}