P1123 取数游戏（dfs算法）-编程知识

P1123 取数游戏（dfs算法）

题目描述

一个 N×M 的由非负整数构成的数字矩阵，你需要在其中取出若干个数字，使得取出的任意两个数字不相邻（若一个数字在另外一个数字相邻 8个格子中的一个即认为这两个数字相邻），求取出数字和最大是多少。

输入格式

第一行有一个正整数 T，表示了有 T 组数据。

对于每一组数据，第一行有两个正整数 N 和 M，表示了数字矩阵为 N 行 M 列。

接下来 N 行，每行 M 个非负整数，描述了这个数字矩阵。

输出格式

共 T 行，每行一个非负整数，输出所求得的答案。

输入输出样例

输入

3
4 4
67 75 63 10
29 29 92 14
21 68 71 56
8 67 91 25
2 3
87 70 85
10 3 17
3 3
1 1 1
1 99 1
1 1 1

输出

271
172
99

数据范围及约定

对于20%20%的数据，1≤N,M≤3；
对于40%40%的数据，1≤N,M≤4；
对于60%60%的数据，1≤N,M≤5；
对于100%100%的数据，1≤N,M≤6，1≤T≤20。

思路：

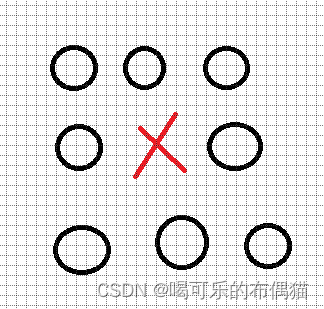
此题为n皇后问题的简单版，算法为dfs，只要枚举每行每列元素就可，分两种情况，取这个元素和不能取这个元素，题目中所说的，相邻的八个格子元素不能取是这个意思如图

×的八个方向不能取。接下来我们看代码

AC代码：

#include<iostream>
#include<cmath>
#include<cstring>using namespace std;int dx[8] = {-1,-1,-1,0,0,1,1,1},dy[8] = {-1,0,1,-1,1,-1,0,1};
const int N = 10;
int g[N][N];//数字数组 
int st[N][N];//标记数组 
int mx,ans,n,m;void dfs(int x,int y)
{//如果搜到该行的最后一列就换下一行第一列 if(y == m + 1){x++,y=1;}//所有行列搜完了 进行输出 if(x == n + 1){mx = max(ans,mx);return; }//不放 dfs(x,y+1);//放if(!st[x][y]){ans += g[x][y];for(int i=0;i<8;i++){st[x+dx[i]][y+dy[i]]++;}dfs(x,y+1);for(int i=0;i<8;i++){st[x+dx[i]][y+dy[i]]--;}ans -= g[x][y];} 
}int main()
{cin.tie(0)->ios::sync_with_stdio(false);//快读 int t;cin >> t;while(t --){//注意：每次使用完记得清0 memset(g,0,sizeof(g));memset(st,0,sizeof(st));cin >> n >> m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin >> g[i][j];}}mx = 0;//每次搜完需要变成0，方便下次使用不会错 dfs(1,1);//从第一个行第一列第一个元素开始搜索 cout << mx << endl;}return 0;
}