day9 | 栈与队列 part-1 (Go) | 232 用栈实现队列、225 用队列实现栈-编程知识

今日任务

栈与队列的理论基础 (介绍:代码随想录)
232 用栈实现队列(题目: . - 力扣（LeetCode）)
225 用队列实现栈 (题目: . - 力扣（LeetCode） )

栈与队列的理论基础

栈 : 先进后出队列: 后进先出

老师给的讲解:代码随想录这个可能适合于 c++的同学理解,我的 go 看这里是有点不明所以..

232 用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

想法:

其实我完全理解栈与队列的特性, 先进后出、先进先出嘛, 但是一开始明白这题让干嘛的,在想这是否跟语言有关啊? 下一步直接看题解Go代码,

问题:

看了题解才明白,其实我们就是可以利用各种语言提供的数据类型, 去模拟实现栈的一个效果,栈就是要具有 push 、pop、top、empty 这几个操作. 然后再用栈去实现队列的操作:push、pop、peek、empty.

那么理解了题意后,才是该思考的问题了,如何用拥有栈特性的数据结构去实现拥有队列属性的数据结构呢??🤔🤔

解决思路:

使用栈来模式队列的行为，如果仅仅用一个栈，是一定不行的，所以需要两个栈一个输入栈，一个输出栈，这里要注意输入栈和输出栈的关系。

就是我们将数据 push 到栈里了,这时该如何将第一个 push 到栈的数据通过 pop给先取出来呢? 我们可以借助另一个栈2,将我们另一个栈的数据全取出来,再 push 到栈 2 里了,这时的栈 2 的元素出栈的顺序就和我们的队列相同了.

图片和题解参考:代码随想录

看代码(Go):

// 先用切片模拟栈,再用两个栈的特性去模拟一个队列的特性
//  1、通过切片实现一个栈的各种操作
type MyStack []intfunc (s *MyStack) Push(v int){*s = append(*s,v)
}func (s *MyStack) Pop() int {val := (*s)[len(*s)-1]*s = (*s)[:len(*s)-1]return val
}func (s *MyStack) Peek() int {val := (*s)[len(*s)-1]return val
}func (s *MyStack) Size() int {return len(*s)
}func (s *MyStack) Empty() bool{return s.Size() == 0
}// 2、下面开始用两个栈实现队列
type MyQueue struct {inStack *MyStackoutStack *MyStack
}func Constructor() MyQueue {return MyQueue {inStack: &MyStack{},outStack: &MyStack{},}
}func (this *MyQueue) Push(x int)  {this.inStack.Push(x)
}// 在取之前,要先把入栈里的元素全都取出放到出栈里(如果出栈里仍有数据的话,肯定还是可以直接出的)
func (this *MyQueue) Pop() int {this.moveStack()return this.outStack.Pop()
}func (this *MyQueue) Peek() int {this.moveStack()return this.outStack.Peek()
}func (this *MyQueue) Empty() bool {return this.inStack.Empty() && this.outStack.Empty()
}func (this *MyQueue) moveStack() {// 如果出栈为空的时候,再将入栈里的数据全都移动到出栈里,这样保证所有数据一直按照先进先出的顺序来的if this.outStack.Empty() {for !this.inStack.Empty() {this.outStack.Push(this.inStack.Pop())}}
}

225 用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

注意：

你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

想法:

做了上一题后,我们就明白该如何去用语言已有的数据结构去模拟出栈的操作,我直接用切片就能实现栈的操作哎,但是题目还是让我们用两个队列实现,主要还是想要我们理解其中该如何转换.

问题:

两个队列该如何实现呢? 如果我们像上一题,一个输入一个输出队列模拟还真不行, 因为最后出来的还都是先进先出.

解决思路:

1、两个队列 (题目要求)

依然还是要用两个队列来模拟栈，只不过没有输入和输出的关系，而是另一个队列完全用来备份的！如下面动画所示，用两个队列que1和que2实现队列的功能，que2其实完全就是一个备份的作用，把que1最后面的元素以外的元素都备份到que2，然后弹出最后面的元素，再把其他元素从que2导回que1.

2、一个队列 (更优)

一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外）重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。

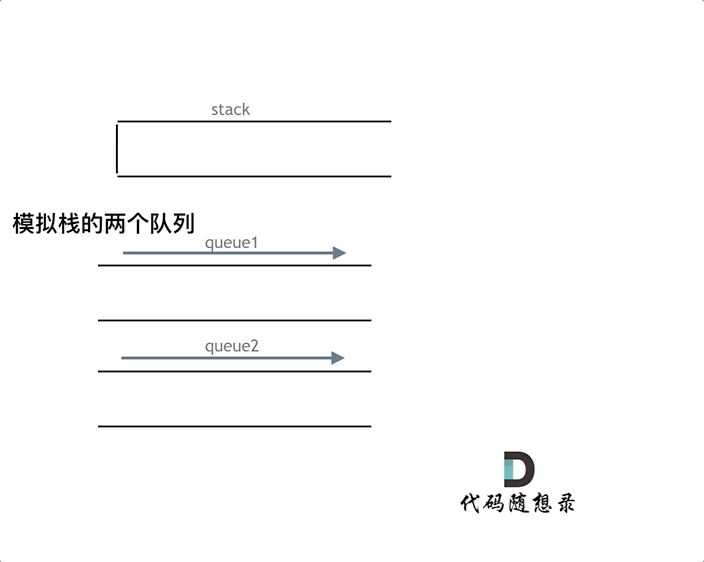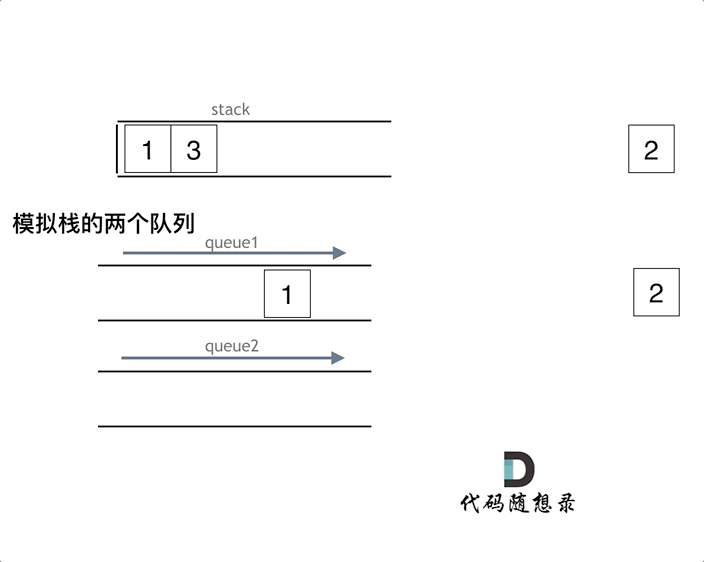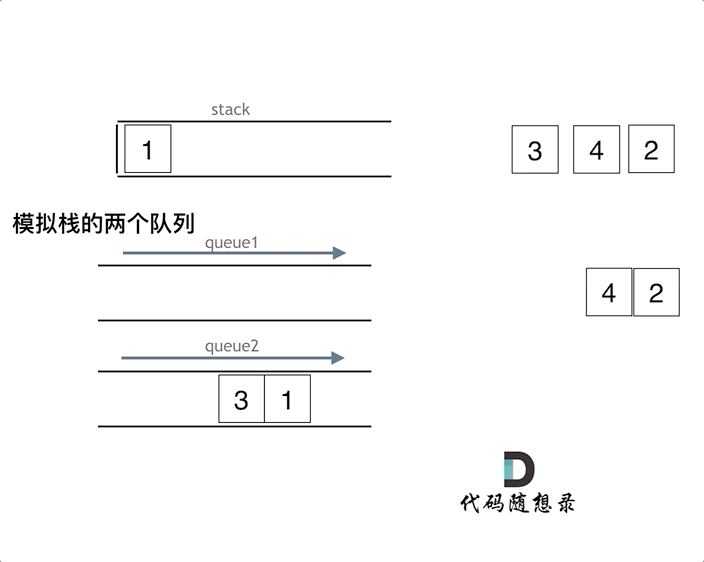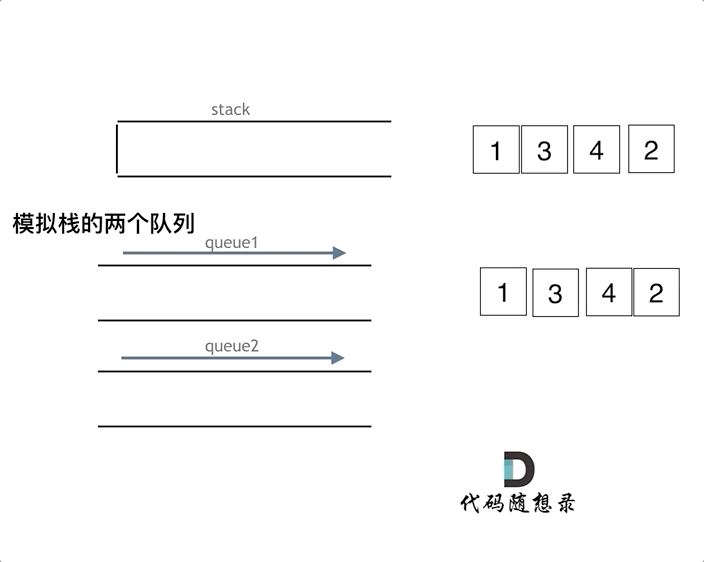
图片和题解参考:代码随想录

// 使用1个 队列实现栈的效果type MyStack struct{  // 初始化queue []int}func Constructor() MyStack {return MyStack{queue: make([]int,0),}}func (this *MyStack) Push(x int){// 添加元素this.queue = append(this.queue,x)
}func (this *MyStack) Pop() int {// 取出元素,因为我们当前是模拟在队列里的,遵守了一个先进先出的顺序,那么为了实现栈,我们要实现后进先出的效果n := len(this.queue)-1  // 判断长度// 除了最后一个元素,其余的都重新添加到队列里for n != 0{val := this.queue[0]// 截掉第一个元素,即将加入到队尾this.queue=this.queue[1:]this.queue=append(this.queue,val)n--}// 弹出元素val := this.queue[0]this.queue = this.queue[1:]return val
}func (this *MyStack) Top() int {val := this.Pop()// 先弹出来,再添加进去,虽然这个过程也挺无语的,就是先来了个 for 循环把最后一个元素取出来了,然后再推进去.this.Push(val)return val
}func (this *MyStack) Empty() bool {return len(this.queue) == 0
}// 两个队列实现的
type MyStack struct {//创建两个队列queue1 []intqueue2 []int
}func Constructor() MyStack {return MyStack{	//初始化queue1:make([]int,0),queue2:make([]int,0),}
}func (this *MyStack) Push(x int)  {//先将数据存在queue2中this.queue2 = append(this.queue2,x)	//将queue1中所有元素移到queue2中，再将两个队列进行交换this.Move() 
}func (this *MyStack) Move(){    if len(this.queue1) == 0{//交换，queue1置为queue2,queue2置为空this.queue1,this.queue2 = this.queue2,this.queue1}else{//queue1元素从头开始一个一个追加到queue2中this.queue2 = append(this.queue2,this.queue1[0])  this.queue1 = this.queue1[1:]	//去除第一个元素this.Move()     //重复}
}func (this *MyStack) Pop() int {val := this.queue1[0]this.queue1 = this.queue1[1:]	//去除第一个元素return val}func (this *MyStack) Top() int {return this.queue1[0]	//直接返回
}func (this *MyStack) Empty() bool {
return len(this.queue1) == 0
}

我这一开始提交的可以直接通过,但是不是队列实现栈,哈哈...

// 我这下面的栈并不是由队列实现的?  感觉有点奇怪,直接就用了下标索引取值的很 easy
type MyStack struct {queue []int
}func Constructor() MyStack {return MyStack{queue: make([]int,0),}
}func (this *MyStack) Push(x int)  {this.queue = append(this.queue,x)
}func (this *MyStack) Pop() int {val := this.queue[len(this.queue) - 1]this.queue = this.queue[0:len(this.queue)-1]return val
}func (this *MyStack) Top() int {return this.queue[len(this.queue) - 1]
}func (this *MyStack) Empty() bool {return len(this.queue) == 0
}