目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
1.算法运行效果图预览



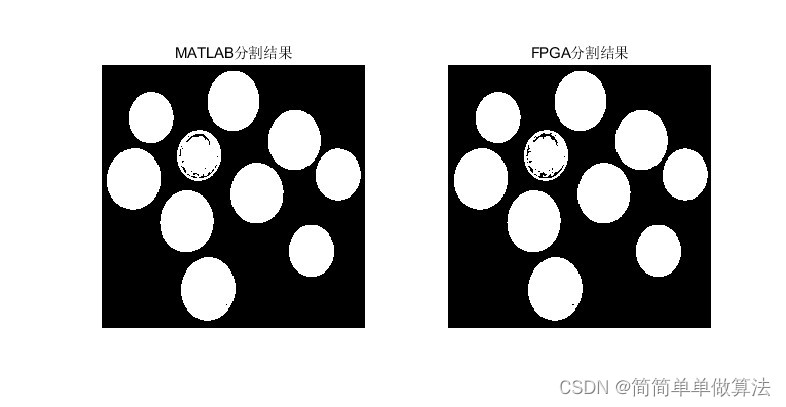
2.算法运行软件版本
VIVADO2019.2
matlab2022a
3.部分核心程序
`timescale 1ns / 1ps
//
// Company:
// Engineer:
// // Design Name:
// Module Name: test_image
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//
//MATLAB/verilog/python/opencv/tensorflow/caffe/C/C++等算法仿真module test_image;reg i_clk;
reg i_rst;
reg i_ready;
reg [7:0] Tmp[0:100000];
reg [7:0] datas;
wire[15:0]o_histb;wire[7:0]o_lvl;
wire[7:0]o_y;integer fids,jj=0,dat;//D:\FPGA_Proj\FPGAtest\code2initial
beginfids = $fopen("D:\\FPGA_Proj\\FPGAtest\\code2\\data.bmp","rb");dat = $fread(Tmp,fids);$fclose(fids);
endinitial
begin
i_clk=1;
i_rst=1;
i_ready=0;
#1000;
i_ready=1;
i_rst=0;
#655350;
i_ready=0;
end always #5 i_clk=~i_clk;always@(posedge i_clk)
begindatas<=Tmp[jj];jj<=jj+1;
endim_hist im_hist_u(
.i_clk (i_clk),
.i_rst (i_rst),
.i_ready (i_ready),
.i_xin (datas),
.o_histb (o_histb),
.o_lvl (o_lvl),
.o_y (o_y)
);//将数据导出,由MATLAB显示图像分割效果
integer fout1;
initial beginfout1 = $fopen("result.txt","w");
endalways @ (posedge i_clk)beginif(jj>=66613+1 & jj<=66613+65536)$fwrite(fout1,"%d\n",o_y);else$fwrite(fout1,"%d\n",0);
endendmodule
0X_033m4.算法理论概述
图像阈值计算和分割是图像处理领域的一项重要任务,它通过设定一个阈值将图像从灰度空间转化为二值空间,从而实现对图像区域的有效划分。基于直方图的阈值选取方法主要依赖于图像的灰度直方图分布特性。
在开始之前,我们需要了解直方图和阈值分割的基本概念:
-
直方图:图像的直方图是表示图像中每个灰度级出现频率的图表。对于灰度图像,直方图显示了从黑到白(通常是0到255)的灰度值分布。
-
阈值分割:阈值分割是指通过一个阈值将图像的像素分为两组(通常是前景和背景),使得两组之间的差异最大化。
5.算法完整程序工程
OOOOO
OOO
O