题解：Minimize Inversions Number

前言

好题。

思路分析

分析一下答案的组成：

令 \(d_i=\sum_{j=1}^{i-1} [p_i<p_j]-\sum_{j=1}^{i-1}[p_i>p_j]\)，\(S\) 表示选出的集合，\(cnt\) 表示集合 \(S\) 的逆序对数，\(tot\) 表示这个序列的逆序对数：

\[tot-\sum_{i \in S} d_i+cnt-(\binom{|S|}{2}-cnt) \]

不难发现问题在于如何决策 \(cnt\) 这一项。

做一点观察：对于任意两个 \(i,j\) 满足 \(i < j,p_i > p_j\)，都满足 \(j\) 优先于 \(i\) 被选择。

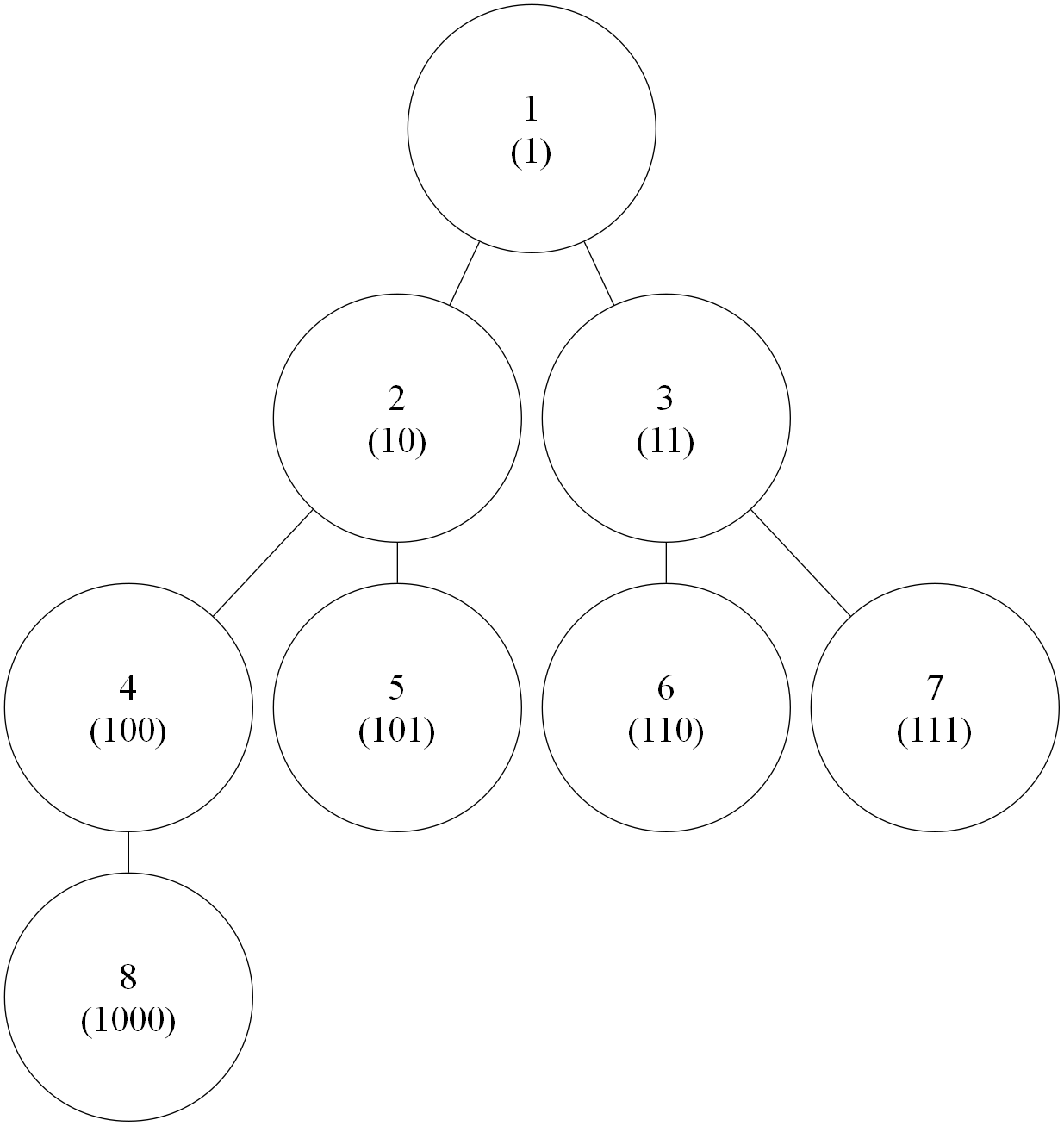
考虑用调整法进行证明，将 \((i,p_i),(j,p_j)\) 画到二维平面上，有：

其中方框中的数字表示这个范围的点，对答案的贡献。

因此，我们总可以找到一个更合适的 \(i\)，使得答案之和最小。

同时，因为调整之后的下标会增加，调整都会在有限步数内结束。

这样我们就证明了结论的正确性。

设 \(s_i = \sum_{j=i+1}^{n} [p_i>p_j]\)，那么不难发现：

\[d_i=(i-p_i+s_i)-(p_i-s_i-1)=i-2p_i+2s_i+1 \]

\[cnt=\sum_{i \in S} s_i \]

所以答案变为：

\[tot-\sum_{i \in S} i-2p_i+1+\binom{|S|}{2} \]

我们惊喜的发现这个式子对于 \(i\) 是独立的！

具体地，我们按 \(i-2p_i+1\) 排序，每次选择前 \(k\) 大即可。

用树状数组求逆序对即可。

总体复杂度 \(O(n \log n)\)。